DERIVADAS
1. Con 200 metros de tela metálica se quiere vallar un terreno de forma rectangular destinado al ganado. Determinar las dimensiones que ha de tener para que se disponga de la máxima superficie.
2. Un vendedor de colecciones de libros recibe de su empresa un salario fijo de 60.000 pesetas, más una cantidad que depende del número de colecciones que venda según la expresión:
1000x-0.25x3 (siendo x el número de colecciones vendidas). Este vendedor tiene unos gastos fijos de 10.000 pesetas al mes más 700 pesetas por cada colección vendida, gastos que corren por su cuenta.
Se pide: i) Obtener la función que expresa los beneficios que obtiene el vendedor
ii) ¿Cuál es el número de colecciones que debe vender para obtener beneficio máximo?
3. Se quiere construir una ventana rectangular de 1 m2 de superficie. Esta ventana se va a rodear de un marco cuyo coste es de 500 pesetas por metro de altura de ventana y 320 pesetas por metro de anchura. ¿Cuáles deben ser las dimensiones de la ventana para que el marco resulte más económico? . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (Junio-97)
4. Se tiene una lona de forma rectangular y 64 m2 de superficie. ¿Cuáles han de ser sus dimensiones para que la suma de los cuadrados de sus lados sea mínima? ¿Ha de tener las mismas dimensiones dicha lona si lo que se desea es que su perímetro sea mínimo? . . . . . . . (Septiembre-98)
5. Una empresa ha realizado un estudio acerca de costes de producción llegando a la conclusión de que producir x unidades de un objeto dado tiene expresado por: f(x)=0.25x2+25x+25. La venta de x unidades de ese producto proporciona unos ingresos dados por la expresión i(x)=(30+0.125x)x, siendo x el número de unidades producidas. Se pide:
i) Hallar el número de unidades que se deben producir para que los costes sean mínimos.
ii) Hallar la expresión de los beneficios obtenidos en función de x, suponiendo que se venden las x unidades producidas.
iii) Hallar el número de unidades que se deben producir y vender para obtener máximo beneficio.
(Junio-97)
6. Un estudio acerca de la presencia de gases contaminantes en la atmósfera de una gran ciudad en los últimos años indica que la concentración de estos viene dada por la función
C(x)=-0.2x2+5x+30 (x en años contando a partir del 1 de enero de 1.990).
i) Halla la tasa de variación entre enero de 1.991 y enero de 1.995
ii) Según el estudio ¿en qué año se alcanzará un máximo en el nivel de contaminación?
iii) ¿En el año 1.997 era creciente C(x)?
iv) Halla la pendiente de la recta tangente a esta función en x=8. Interpreta el resultado obtenido.
(Septiembre-98)
7. Una persona amante de las Matemáticas desea donar sus 3.600 libros a dos bibliotecas A y B. Sus instrucciones son que los lotes de libros se hagan de manera que el producto del número de libros destinados a la biblioteca A por el cubo del número de libros destinados a la biblioteca B sea máximo. Determina la cantidad de libros recibida por cada biblioteca. . . . . . . . . . . . . . . (Junio-99)
8. Se ha estudiado el rendimiento de los empleados de una oficina a medida que transcurre la jornada laboral (Dicho rendimiento corresponde al número de instancias revisadas en una hora). La función que expresa dicho rendimiento es: R(t)=30t-10,5t2+t3, siendo t el número de horas transcurridas desde el inicio de la jornada laboral.
i) Determina cuándo se produce el máximo rendimiento y cuándo el mínimo rendimiento.
ii) Halla la tasa de variación media del rendimiento R(t) entre t=2 y t=4. . . . . . . . . . (Septiembre-99)
9. Dada la función f(x)=2x3+3x2-12x+4. Se pide:
i) Pendiente de la recta tangente a la gráfica de la función en el punto de abcisa x=2.
ii) Escribir los intervalos, en donde la función sea creciente y en donde sea decreciente.
iii) Determinar los valores x en los que la función f alcanza un máximo relativo y un mínimo relativo, respectivamente ¿Cuánto vale la función f en esos puntos?. . . . . . . . . . . . . . . (Junio-2.000)
10. El consumo de agua en un colegio viene dado por la función:
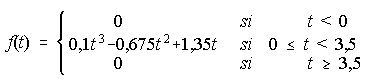
en donde t es el tiempo en horas a contar desde la apertura del colegio y f(t) es el consumo en m3. Se supone que la jornada escolar comienza a las 10 horas y termina a las 13,5 horas. Se pide:
i) ¿Cuándo el consumo de agua es creciente? ¿Cuándo el consumo de agua es decreciente?
ii) ¿En qué momento el consumo de agua es máximo y en qué momento es mínimo?
(Septiembre 2.000)
11. Tras la aparición de una cierta enfermedad infecciosa, el número de afectados viene dado por la función p(t)=48t2-3t3, siendo t el número de días desde que se detectó el primer caso. Se pide:
i) ¿Cuántos días transcurrirán hasta que la enfermedad deje de propagarse?
ii) ¿Cuándo aumenta el número de personas afectadas? ¿Cuándo disminuye?
iii) ¿Cuándo se detecta el número máximo de personas afectadas? ¿Cuántas son las personas afectadas en ese momento? . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (Propuesto 2.000)
12. Se dispone de un papel rectangular de 2 m2 de superficie para diseñar un cartel publicitario. Los márgenes del cartel han de ser 0,2 metros el superior, 0,1 metros el inferior, 0,1 metros el izquierdo y 0,05 metros el derecho. Calcula las dimensiones que debe tener el papel para que la parte que se ha de imprimir sea máxima. ¿Qué superficie tendría la parte impresa? . (Propuesto 2.000)
13. Halla un número "xy" tal que la suma de sus cifras sea 12 y de modo que la suma del cubo de la cifra de las decenas y del triple del cuadrado de la cifra de las unidades sea lo más pequeña posible. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ( Junio 2.001)
14. El precio, en pesetas, que la acción de una empresa alcanza en el transcurso de una sesión de Bolsa, viene dado por la función p(t)=40t3-420t2+1200t+200, en donde t es el tiempo en horas a contar desde el inicio de la sesión. Supongamos que la sesión comienza a las 10 de la mañana y finaliza a las 7 horas de la tarde. Se pide: (a) ¿Entre qué horas el precio de la acción sube? (b) ¿Entre qué horas el precio de la acción baja? (c)¿A qué hora el precio de la acción alcanza un máximo relativo? ¿Cuál es este valor? (d) ¿A qué hora el precio de la acción alcanza un valor mínimo relativo? ¿Cuál es este valor? (e) ¿A qué hora el precio de la acción alcanza su valor más grande? ¿Cuál es este valor? . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (Septiembre 2.001)
15. Se considera la función f(x)=3x4+4x3-12x2+1. Se pide: a) Pendiente de la recta tangente a la gráfica de la función en el punto de abcisa x=-1. b) Escribe los intervalos en donde la función sea creciente y en donde sea decreciente. c) Determina los valores de x en los que la función alcanza máximos y mínimos relativos. d) Valor máximo que toma la función en el intervalo [-1,-2].
(Propuesto 2.001)
16. Una cuerda de 120 metros de longitud se divide en dos trozos. Con el primero de ellos se forma un cuadrado de lado "x" y con el segundo se forma un rectángulo de base "x" y de altura "y". Halla los valores "x e y" para que la suma del área del cuadrado y el doble del área del rectángulo sea lo mayor posible y calcula este valor máximo.
(Propuesto 2.001)
SOLUCIONES
1. Cuadrado de lado 50 metros.
2. i) f(x)=-0.25x3+300x+50000 ii) 20 colecciones.
3. 0.80 metros de alto y 1.25 metros de ancho.
4. Un cuadrado de 8 metros de lado. Si.
5. i) 0 unidades. ii) f(x)=-0.125x2+5x-25 iii) 20 unidades.
6. i) 3.8 ii) En el año 2.002 iii) Si iv) 1.8. La contaminación está creciendo.
7. Debe donar 900 libros a la biblioteca A y 2.700 a la B.
8. i) Máximo rendimiento en t=2, mínimo rendimiento en t=5. ii) -5.
9. i) 24 ii) Crece: (-inf,-2) (1,inf). Decrece: (-2,1). iii) Máximo en (-2,24) Mínimo en (1,-3)
10. i) Creciente desde las 10 horas hasta las 11,5 horas y desde las 13 horas hasta las 13,5 horas.
Decreciente desde las 11,5 horas hasta las 13 horas.
ii) Consumo máximo a las 11,5 horas. Consumo mínimo a las 13 horas.
11. i) 16 días ii) Aumenta hasta el día 10'67. Disminuye desde el día 10'67.
iii) Número máximo el día 10'67. Aproximadamente 1.820 personas (1.820'44).
12. La base debe tener 1 m y la altura 2 m. La superficie impresa es de 1,445 m2.
13. El número es el 48.
14. a) Crece de 10 a 12 y de 15 a 19 horas. . . . . b) A las 12 horas. 1.240 pts.
c) A las 15 horas. 700 pts. . . . . . d) A las 19 horas. 1.740 pts.
15. a) m=24 . . . . . . . . . . . . . . . b) Crece:(-2,0)u(1,inf); decrece (-inf,-2)u(0,1)
c) Mínimos (-2,-31) y (1,-4); Máximo (0,1). . . . . . . . d) 1
16. x=12 y=24.