FUNCIONES

1. Dada la función siguientes, se pide:

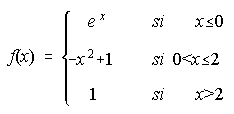
i) Representar gráficamente f(x). . . . . . . . . . . . . . . . . . . . . . . . . . ii) Estudiar su continuidad.

iii) Estudiar crecimiento y decrecimiento.

iv) Determinar la pendiente de la recta tangente a f(x) en x=1.

2. Los costes de fabricación de un producto vienen expresados por C(x), coste en miles de pesetas en función de x, número de artículos fabricados:

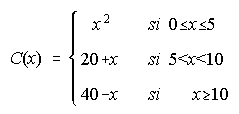
Se pide: i) Representar gráficamente C(x). . . . . . . . . . . . . . . . . . . . . . ii) Estudiar su continuidad.

iii) Hacer un breve comentario acerca de la variación del coste en relación con las unidades producidas.

3. Suponiendo que el rendimiento r en % de un estudiante que realiza un examen de una hora venga dado por: r(t)=300t(1-t) siendo 0<t<1 (tiempo en horas). Se pide:

i) Representar gráficamente la función r(t).

ii) Indicar cuándo aumenta o disminuye el rendimiento. ¿Cuándo se anula?

iii) ¿Cuándo es máximo el rendimiento y cuál es?

4. Dada la función f(x) siguiente, se pide: i) Representa gráficamente. ii) Estudia su continuidad. iii) Halla el área limitada por f(x) y el eje OX.

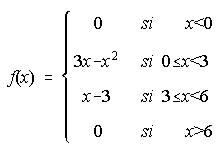
5. Dada la función f(x) siguiente, se pide:

i) Represéntala gráficamente. . . . . . . . . . . . . . . . . . . . . . . . . . ii) Estudiar su continuidad.

iii) Hallar la pendiente de su recta tangente en x=4.

6. En el mercado financiero hay unos fondos de inversión cuya rentabilidad, en función de la cantidad x invertida (en miles de pesetas), viene expresada por la función:

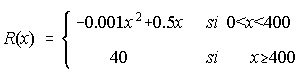
i) Deducir cuál es la cantidad x, en miles de pesetas, que conviene invertir para obtener máxima rentabilidad y hallar el valor de esta rentabilidad.

ii) Justificar entre qué cantidades invertidas es creciente la rentabilidad.

iii) ¿Cuál es el valor de la pendiente de la recta tangente a R(x) para x=300? ¿Y para x=450? Interpreta estos resultados.

(Septiembre-97)

7. La función f(x) representa la cotización de unos determinados valores en bolsa a lo largo de un mes (30 días): f(x)=0.2x²-8x+100 (siendo x el número de días transcurridos de ese mes).

i) Dibujar la gráfica de esta función.

ii) ¿En qué días del mes estuvieron bajando los valores, y en qué días estuvieron subiendo?

iii) ¿Cuáles fueron estos valores máximo y mínimo respectivamente?

8. Dada la función f(x)=x²-1

i) Dibuja su gráfica y la de f(x) . . . . . . . . . . . ii) Calcula la pendiente de su recta tangente en x=3.

iii) ¿Cuál es el valor del área limitada por -f(x)=-x²+1 y el eje OX?

9. Dada la función f(x) siguiente se pide:

i) Gráfica de la misma. . . . . . . ii) Estudiar su continuidad y hallar a para que sea continua en x=4.

iii) Determinar intervalos de crecimiento y decrecimiento.

iv) Hallar la pendiente de la recta tangente a f(x) en x=3 y x=5.

10. Dada la función siguiente, se pide:

i) Gráfica de f(x). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ii) Estudia la continuidad de f(x).

iii) Halla el área limitada por f(x), el eje OX y las rectas x=0 y x=3.

(Junio-99)

11. Dada la función siguiente, se pide:

i) Gráfica de f(x). . . . . . . . . . . . . . . . . . . . . . . . . ii) Estudia la continuidad y derivabilidad de f(x).

iii) Calcula la pendiente de la recta tangente a f(x) en el punto de abcisa 4. . . . . . . . (Septiembre-99)

12. Dada la función f(x) siguiente, se pide:

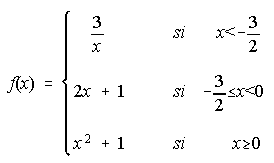
Se pide: i) Estudiar la continuidad de f. . . . . . . . . . . . . . . . . . . . . ii) Representación gráfica de f.

iii) Área del recinto limitado por la gráfica de f, el eje 0X y la recta x=3.

(Junio-2.000)

13. Dada la función f(x) . Se pide: i) Estudiar la continuidad de la función.

ii) Representación gráfica de f.

iii) Calcular el área del recinto plano limitado por la gráfica de f, el eje 0X, el eje OY y la recta x=3.

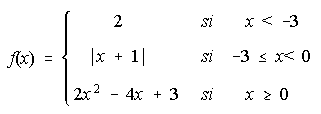
(Septiembre 2.000)

14. Dada la función f(x). Se pide:

i) Determinar el valor de "a" para que f sea continua en x=0.

ii) Para el valor de "a" calculado en el apartado anterior, dibujar la gráfica de la función.

iii) Calcular el área del recinto plano limitado por la gráfica de la función f, el eje OX y las rectas x=-1 y x=1.

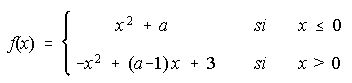
(Propuesto 2.000)

15. Dada la función . Se pide: i) Determinar el valor de "a" para que f sea continua en x=0.

ii) Para ese valor de "a" ¿Es f continua en todo valor real de x?. . . . . . . . . . . . iii) Gráfica de f.

iv) Área del recinto limitado por la gráfica de f, el eje OX y las rectas x=1 y x=2.

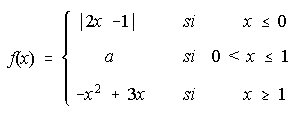
(Propuesto 2.000)

16. Dada la función 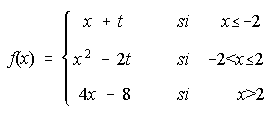. Se pide:

a) Halla el valor de "t" para que la función sea continua en todos los números reales.

b) Para el valor de "t" obtenido en el apartado anterior, representa gráficamente la función f(x).

c) Para el valor de "t" obtenido en el apartado a) calcula el área del recinto cerrado limitado por la gráfica de f(x) y el eje OX. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (Junio 2.001)

17. Dada la función 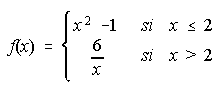. Se pide:

a) Estudiar la continuidad de f. . . . . . . . . . . . . . . . . . . . . . . . . . . . b) Representación gráfica de f.

c) Área del recinto cerrado que delimita la gráfica de f y el eje 0X. . . . . . . . . . . . (Septiembre 2.001)

18. Dada la función 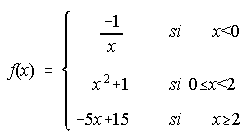. Se pide:

a) Estudia la continuidad de f(x). . . . . . . . . . . . . . . . . . . . . . . . b) Representación gráfica de f(x).

c) Área del recinto limitado por la gráfica de f(x), los ejes de coordenadas y la recta x=2.

(Propuesto 2.001)

19. Dada la función 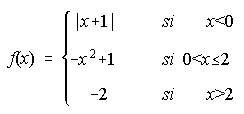. Se pide:

a) Estudia la continuidad de f(x). . . . . . . . . . . . . . . . . . . . . . . . . b)Representación gráfica de f(x).

c)Calcula el área del recinto cerrado que delimita la gráfica de la función con el eje OX.

(Propuesto 2.001)

SOLUCIONES

1. ii) No es continua en x=2 . . . . iii) Crece en (-inf,0) Decrece en (0,2) Constante en (2,inf)

iv) -2

2. ii) Continua en [0,40]

iii) Con menos de 5 unidades el coste aumenta rápido, luego de 5 a 10 unidades el coste aumenta, pero menos y con más de 10 unidades los costes disminuyen.

3. ii) Aumenta hasta la media hora y después disminuye.

iii) El rendimiento máximo es a la media hora que es del 75%.

4. ii) No es continua en x=6 . . . . . iii) 9 u².

5. ii) No es continua en x=3. . . . . iii) 5

6. i) 250.000 pesetas y se obtiene 62.500 pesetas.

ii) De 0 a 250.000 crece, de 250.000 a 400.000 decrece y a partir de 400.000 es constante.

iii) -0.1 y 0. En 300 la rentabilidad disminuye, en 450 la rentabilidad es constante.

7. ii) Estuvieron bajando hasta el día 20 y subiendo desde el día 20 hasta el 30.

iii) El valor mínimo es 20 y el máximo es 40.

8. ii) 6 . . . . . iii) 4/3

9. ii) Es continua si a=0.5 . . . iii) Decrece en (-inf,-1) y (1,4). Crece en (-1,1).Constante en (4,inf)

iv) -2/9. 0

10. ii) No es continua en x=-1/2 ni en x=3 (tiene dos saltos finitos). . . . . . iii) 9/2 u².

11. ii) No es continua en x=3. No es derivable en x=0 y x=3. . . . . . . . . . . iii) -5.

12. i) Es continua en todo R . . . . . . iii) A=49/4 u².

13. i) No es continua en x=0 . . . . iii) A=9 u².

14. i) a=3. . . . . . . iii) A=7 u².

15. i) a=1 . . . . . . ii) No. . . . . . . iii) A=13/6 u².

16. a) t=2 . . . . . . . c) 32/3 u² .

17. a) Es continua. . . . . c) 4/3 u².

18. a) No es continua en x=0. . . . . . c) 14/3 u².

19. a) No es continua en x=2. . . . . . c) 7/6 u².