-- GEOMETRÍA --
1. Halla las ecuaciones paramétricas y continuas de las rectas:
a) pasa por A(1,0,-2) con vector director v=(2,1,-3).
b) pasa por B(2,0,-2) con vector director v= (-1,-1,5).
2. Ecuaciones de las rectas que pasan por:
a) A(3,0,1) y B(2,-3,0) . . . . . . . . . . . . . . . b) C(-3,-1,2) y D(0,-1,0)
3. Halla las ecuaciones paramétricas de las siguientes rectas:
4. Halla las ecuaciones paramétricas y cartesianas de los ejes y planos coordenados.
5. Ecuación del plano que pasa por los puntos A(1,1,2), B(-1,3,5) y C(4,-3,8).
6. Escribe la ecuación paramétrica del plano 3x + 2y - 7z = 9.
7. Dada la recta r: 
, halla las ecuaciones de dos planos que determinen r.
8. Halla los puntos de corte de las siguientes rectas y planos:
a) 
con los planos coordenados.
b) la recta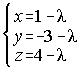 
con el plano x - y + 3z + 1 = 0.
c) la recta del apartado a) con el plano 3x - 2y - 5z + 7 = 0.
9. Los puntos A(1,2,0), B(5,3,0) C(2,6,0) y D(3,4,3) son los vértices de un tetraedro. Comprueba que los puntos medios de los segmentos AB, BD, DC, CA son los vértices de un paralelogramo y por lo tanto están en un mismo plano. Halla la ecuación de este plano y Comprueba que es paralelo a las aristas CB y AD.
10. Estudia la posición relativa de las siguientes rectas:
a) 
b) 
11. Dadas las rectas 
a) Halla k para que se corten en un punto. . . . . . b) Halla la ecuación del plano que determinan.
12. Determina k para que las rectas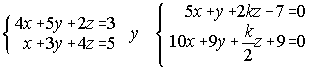 
sean
paralelas.
13. Halla la ecuación del plano que pasa por A(1,0,1) y es paralelo a las rectas
14. Dada la recta r: 
: . . . a) Halla la ecuación de dos planos que determinen r.
b) De todos los planos que pasan por r, halla la ecuación del que pasa por A(0,-3,2).
15. Prueba que las rectas 
determinan un
plano y estudia la posición relativa de este plano con la recta 
.
16. Se consideran las rectas r, s, t de ecuaciones paramétricas:
r: x = 1 + 2a , y = 3 - a , z = 1 + a . . . . . . s: x = 2 - 4b , y = 1 + 2b , z = -2b
t: x = 1 + 4c , y = 1 + c , z = 3 + c
a) Discute dos a dos la posición relativa de estas dos rectas.
b) Cuando dos de ellas determinen un plano, halla la ecuación del mismo.
17. Se consideran las rectas 
, determina el valor de
a para que estén en un mismo plano. Obtén la ecuación de este plano.
18. Escribe la ecuación del plano que pasa por el origen y es paralelo a las rectas
19. Dados los puntos A(1,0,2), B(0,1,3), C(-1,2,0) y D(2,-1,3), halla la ecuación del plano que contiene a la recta que pasa por AB y es paralelo a la recta que pasa por CD.
20. Determina "m y n" para que sean paralelos los dos planos siguientes:
3x - my + 4z + 9 = 0 y 9x - 3y + nz - n = 0.
21. Siendo r la recta determinada por las ecuaciones 
y el plano definido por :
p: 2x + y + mz = n, determina "m y n" de modo que:
a) r y p sean secantes. . . . b) r y p sean paralelos. . . . c) r esté contenido en p.
22. Halla la ecuación de la recta que pasa por el origen y corta a las rectas: 
y
s: x = 2y = z - 1.
23. Halla la ecuación de la recta que pasa por A(1,1,2) y corta a las rectas:
24. Estudia según los valores del parámetro la posición de los siguientes planos:
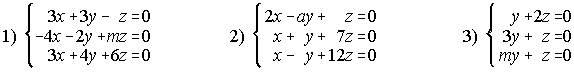
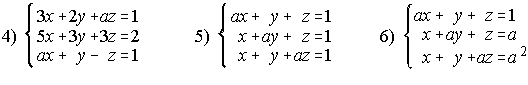
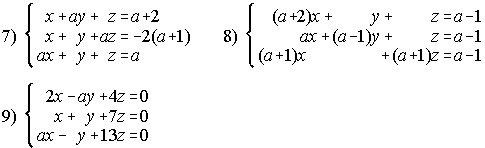
25. Se consideran las rectas r y s . Determina "a" para que se corten. ¿Pueden ser coincidentes?
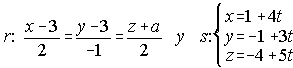
26. Determina "a" para que las rectas 
estén situadas en
un mismo plano. Halla la ecuación de éste.
27. Dados los vectores 
, calcula:
28. Halla la ecuación de la recta que pasa por el punto P(2,-5,3) y es perpendicular al plano
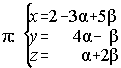
29. Halla el plano perpendicular que pasa por el punto medio de los puntos (2,1,-3) y (-4,2,2).
30. Halla tomando dos a dos la distancia entre los puntos A(2,1,-3), B(0,4,-1) y C(2,3,7).
31. Calcula la distancia del punto (2,-1,3) al plano 3x+2y+3z+5=0.
32. Distancia al plano (x,y,z,)= (2,0,3)+a(-4,9,2)+b(5,-3,8) del punto (0,-5,2).
33. Distancia entre los planos 2x+5y-z+5=0 y 2x+5y-z+9=0.
34. Distancia del punto (-2,1,3) a la recta 
.
35. Distancia entre las rectas: . . .a) 
b) 
36. Distancia de la recta 
al plano 2x-y-z+6=0.
37. Dados los puntos A(3,1,-2), B(4,0,-4), C(4,-3,3) y D(6,-2,2), halla el ángulo que forman las rectas AB y CD.
38. Ángulo entre la recta 
y el plano 2x+7y-6z+1=0.
39. Ángulo entre los planos 2x-y+z-7=0 y x+y+2z-11=0.
40. Calcula el área del triángulo de vértices A(1,0,3), B(-2,5,4) y C(-1,4,7).
41. Calcula el volumen del tetraedro de vértices (1,1,1), (2,-1,3), (5,4 -2) y (3,-7,5).
42. Determina la ecuación de la recta que pasa por el punto P(1,2,2) y es perpendicular a las
rectas de ecuaciones: 
43. Halla la ecuación del plano que pasa por el punto A(1,0,2), es paralelo a la
recta
y es perpendicular al plano 2x-y+z-1=0.
44. Halla el simétrico del punto (0,1,4) respecto de :
a) El punto (-1,2,3). . . . b) La recta 
. . . . c) El plano 4x-2y-3z+4=0.
45. Dadas las rectas r1 y r2 determina dos punto P y Q en r1 y r2 respectivamente para que el vector PQ sea perpendicular a ambas rectas. Calcula la distancia entre esas rectas.
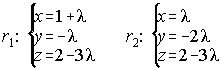
46. Calcula la ecuación del plano paralelo a las rectas 
y que determine con los planos coordenados un tetraedro de volumen 3.
47. Un tetraedro tiene tres vértices A(2,1,0), B(3,4,0) y C(5,1,0) en el plano OXY y el cuarto
vértice D sobre la recta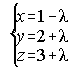 
, halla las coordenadas del cuarto vértice D para que el
volumen del tetraedro valga 6.
48. Las rectas r1, r2 y r3 determinan tres puntos de corte A,B y C respectivamente sobre el plano p: 5x-4y+7z+1=0. Halla el área del triángulo ABC.
49. Determina un punto de la recta 
que equidiste de los planos
3x+4y-1=0 y 4x-3z-1=0. ¿Es única la solución?.
50. Halla la ecuación del plano paralelo al de ecuación 2x-2y+z-8=0 y que equidiste 6 unidades del mismo.
51. Halla la ecuación del plano que pasando por A(0,2,0) y B(0,0,2) corte al eje OX en un punto C tal que el área del triángulo ABC valga 4 unidades.
52. Halla el volumen del tetraedro que forman los planos y=0; z=0; x-y=0 y 3x+2y+z-15 =0
53. Un tetraedro tiene de vértices A(1,1,1), B(-2,1,0), C(2,3,-1) y D(4,6,-5). Halla la longitud de la altura correspondiente a la cara ABC.
54. Halla un punto del plano y=0 que esta sobre la recta que siendo perpendicular al plano del triángulo (0,0,0), (1,0,0) (1,1,1) pasa por el baricentro de este triángulo.
55. Halla la ecuación del plano perpendicular a la recta de ecuación 
y que dista 1
unidad del origen de coordenadas. ¿Existe una única solución?.
56. Un cubo (exaedro regular) tiene los vértices de una de sus caras en los puntos de coordenadas A(3,0,0), B(0,3,0), C(-3,0,0), D(0,-3,0) y los otros cuatro vértices A', B', C' y D' tienen su tercera coordenada positiva (siendo AA', BB', CC' y DD' aristas del cubo).Se pide:
a) Determina razonadamente las ecuaciones de las seis caras del cubo y las de los planos ACB' y BDA'.
b) Determina el coseno del ángulo formado por los dos últimos planos citados.
57. Se considera el plano de ecuación x+3y+z=7, y los puntos A(1,1,1) y B(2,1,-1). Se pide:
a) Mira que A y B están al mismo lado del plano.
b) Encuentra el punto C situado sobre la perpendicular al plano que pasa por B, a igual distancia del plano que B, paro al otro lado (es decir, C es el simétrico de B respecto del plano).
c) Determina el punto D en que la recta AC corta al plano.
d) Mira que D es el punto del plano cuya suma de distancias a A y B es mínima.
58. Encuentra la ecuación del plano paralelo al de ecuación x+y+z=1, determinado por la condición de que el punto A(3,2,1) equidiste de ambos.
59. Encuentra los puntos situados a distancia 5 del origen y pertenecientes a la recta que pasa por A(1,2,5) y B(6,5,6).
60. Sean los planos pt de ecuación: (1+2t)x + (1-t)y + (1+3t)z +2t - 1 = 0 para cada t.
Demuestra que todos los planos pt pasan por una recta r y halla la distancia entre la recta r y la
recta s:
.
61. Halla el volumen del tetraedro de vértices A(0,a,a), B(a,0,a), C(a,a,0) y D(a,a,a).
62. Estudia la compatibilidad del sistema: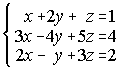 
. Si las ecuaciones del mismo
representan, respectivamente a los planos P1, P2, P3, aplica el estudio que acaba de hacerse para
decidir si:
a) los tres planos son incidentes.
b) el vector 
es paralelo a los tres planos (siendo p1 y p2 los vectores característicos de
los planos P1, P2). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (Junio 88)
63. Dados los puntos del espacio tridimensional: P(4,0,-1); Q(2,2,3), se pide:
a) la ecuación del plano , sabiendo que Q es simétrico de P respecto de dicho plano.
b) la ecuación del plano paralelo al anterior e incidente con P. . . . . . . . . . . . . . . . . (Septiembre 88)
64. Estudia la posición relativa de los siguientes planos según los valores del parámetro a :
p1: ax + y + z = 1 p2: x + ay + z = 1 p3: x + y + az = 1 . . . . (Junio 89)
65. Razona si los puntos A(0,-1,2), B(1,3,4), C(0,1,7) y D(1,-1,2) son coplanarios o son los vértices de un tetraedro. Si forman un tetraedro, halla su volumen. . . . . . . . . . . . . . . . (Junio 89)
66. Dadas las rectas 
. Comprueba razonadamente
que se cruzan. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (Junio 89)
67. Sean los puntos A(1,1,1), B(3,0,2), C(5,-2,2) y D(2,1,t). Halla t para que los cuatro puntos determinen un plano. Halla el área del polígono ABCD para el valor de t hallado previamente.
(Junio 89 y Junio 90)
68. Dadas las rectas 
que se cruzan, se pide
determina el plano paralelo a ambas y equidistante de ambas. . . . . . . . . . . . . . . . (Septiembre 89)
69. Dados los puntos A(3,-2,0) y B(1,-2,-2) y la recta r: x = y = z. Calcula la distancia desde el punto B al plano que contiene a r y al punto A. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (Junio 90)
70. Ecuación del plano que pasa por el punto P(-1,1,2), es perpendicular al plano
x - y - 2z = 0 y paralelo a la recta 
. . . . . . . . . . . . . . . . . . . . . . (Septiembre 90)
71. Obtén la ecuación de un plano que contenga a la recta r y sea perpendicular al plano p, siendo:
. . . . . . . . . . . . . . . . . . . . . . . . . . . . (Junio 91)
72. Calcula "t" para que las rectas r y s se corten en un punto. Encuentra ese punto.
. . . . . . . . . . . . . . . . . . . . . . . . (Junio 91)
73. Determina las ecuaciones de la recta simétrica de la recta r: x-1 = y-2 = z-3 respecto del punto P(3,2,1). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (Septiembre 91)
74. A(1,3,2) y B(2,5,1) son dos vértices de un triángulo que tiene su tercer vértice situado en un
punto arbitrario (variable) de la recta: 
. Calcula el área de los diferentes
triángulos formados por A, B y el tercer vértice en r. ¿El valor de dicha área depende de donde se
sitúe el tercer vértice?. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (Septiembre 91)
75. Halla la ecuación del plano que pasa por los puntos A(5,0,1): B(4,1,0) y es paralelo a la recta
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (Junio 92)
76. Calcula la distancia entre las rectas r y s siendo:
. . . . . . . . . . . . . . . (Junio 92)
77. Determina t para que las rectas r y s se corten en un único punto. Obtén el punto de corte.
. . . . . . . . . . . . . . . (Septiembre 92)
78. Halla la ecuación del plano que es perpendicular al plano 2x - y + 3z -1= 0, paralelo a la
recta 
, y pasa por P(1,1,1). . . . . . . . . . . . . . . . . . . . . . . . . . . . (Septiembre 92)
79. Estudia la posición relativa de los siguientes planos: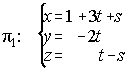
y de
p2: x + 2y + z + 3 = 0. Calcula la distancia entre ambos planos. . . . . . . . . . . . . . . (Junio 93)
80. Estudia si los puntos A(2,-1,0); B(3,0,1) y C(-1,2,1) están alineados. Calcula "a y b" para que el punto D(a,b+1,2) pertenezca a la recta AB. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (Junio 93)
81. Halla la ecuación del plano que contiene a la recta 
y pasa por los puntos
P(1,0,-1) y Q(2,1,2). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (Septiembre 93)
82. Dados los puntos A(1,2,3), B(0,1,1), C(-1,2,0) y D(0,1,3). Estudia si son coplanarios. Si no lo fueran, obtén el volumen del tetraedro que forman. Halla la distancia de C al plano determinado por A,B,D. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (Septiembre 93)
83. Encuentra la ecuación del plano que contiene a la recta r y es paralelo a la recta s:
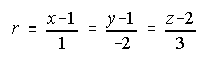
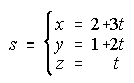. . . . . . . . . . . . . . . (Septiembre 2.000)
84. a) Define cuándo dos vectores de R3 son perpendiculares u ortogonales.
b) Determina el valor de "a" para que sean perpendiculares las rectas:
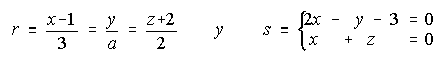
(Septiembre 2.000)
85. Dada la recta
y el punto A(-1,3,2). Se pide:
a) Halla unas ecuaciones paramétricas de la recta "s" que pasa por A y es paralela a "r".
b) Calcula la distancia de "s" a "r". . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (Propuesto 2.001)
86. Dado el punto A(1,1,0) y el plano 2x+y+z=1, calcula:
a) Ecuaciones paramétricas de la recta "r" que pasa por A y es perpendicular al plano.
b) Ecuación del plano que pasa por A y es paralelo al plano.
c) El punto simétrico de A respecto del plano. . . . . . . . . . . . . . . . . . . . . . . . . . . (Propuesto 2.001)
87. Dadas las rectas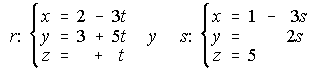 
, se pide:
a) Estudia la posición relativa de las rectas "r" y "s".
b) En el caso en que se corten, calcula las coordenadas del punto de corte. . . . . (Propuesto 2.001)
88. Dadas las rectas 
a) Calcula el valor de "a" para que las rectas "r" y "s" sean perpendiculares.
En el caso de que "r" y "s" se corten:
b) Calcula las coordenadas del punto de intersección de las rectas "r" y "s".
c) Halla la ecuación del plano que determinan las rectas "r" y "s". . . . . . . . . . . . . (Propuesto 2.001)
SOLUCIONES
1. a) x=1+2t; y=t; z=-2-3t. . . . .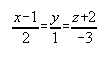 
b) x=2-t; y=-t; z=-2+5t.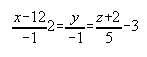
2. a) x=3+t; y=3t; z=1+t. . . . . . b) x=3t; y=-1; z=-2t.
3. a) x=t; y=1+2t; z=-1-t. . . . . . b) x=t; y=3+3t; z=-3-t.
5. 24x+21y+2z-49=0 . . . . . . . . 6. x=3-2t+7s; y=3t; z=3s. . . . . . 7. 2x-3y+7=0; 4x-3z+8=0
8. a) Con 0XY (-1/5,-9/5,0) Con 0XZ (1,0,3) Con 0YZ (0,-3/2,1/2)
b) (-14/3,-26/3,-5/3) . . . . c) (3/5,-3/5,2)
9. 6x+6y-8z-33=0 . . . . . . 10. a) Se cruzan . . . . . b) Se cruzan .
11. a) k=28/5 . . b) 11x-5y+7z+6=0 . . . . . 12. k=4 . . . . . 13. 11x-8y+2z-13=0
14. a) 2x-3y+7=0; 2y-z-2=0 . . . . b) 6x-y-4z+5=0
15. Plano: 5x-2y-z+2=0; La recta y el plano son paralelos.
16. a) r y s paralelas; r y t se cruzan; s y t se cruzan; . . . . b) x+y-z-3=0
17. a=-4 . . . . . y-z-2=0 . . . . . 18. x-2y+z=0 . . . . . . 19. x+y-1=0 . . . . . 20. m=1; n=12
21. a) m-23/7, n cualquiera . . . b) m=-23/7, n9/7 . . . c) m=-23/7, n=9/7
22. x=2t; y=-t; z=t . . . . . . 23. x=1+t; y=1; z=2-t
24. 1) Si m no es 46/3 se cortan en (0,0,0). . . . Si m=46/3 se cortan en una recta.
2) Si a no es -36/5 se cortan en (0,0,0). . . . . . . Si a=-36/5 se cortan en una recta.
3) Se cortan en una recta.
4) Si a no es 1 ni 8/3 se cortan en un punto. . . . Si a=1, se cortan dos a dos. . . Si a=8/3, se cortan dos a dos.
5) Si a no es 1 ni -2 se cortan en un punto . . . . .Si a=1, son coincidentes . . . . Si a=-2, se cortan dos a dos.
6) Si a no es 1 ni -2, se cortan en un punto . . . . Si a=1, son coincidentes . . . . Si a=-2, se cortan dos a dos.
7) Si a no es 1 ni -2, se cortan en un punto . . . . Si a=1, son paralelos . . . . . . .Si a=-2, se cortan dos a dos.
8) Si a no es 0 ni ±1, se cortan en un punto . . . Si a=0, se cortan dos a dos . . . Si a=1, dos coincidentes, otro los corta . . . . Si a=-1, no existe el tercer plano.
9) Si a no es 3 ni -12/7, se cortan en un punto . . Si a=3, se cortan en una recta . . .Si a=-12/7, se cortan en una recta.
25. a=1. . No . . . . . . . . . 26. a=-4 . . . x-5y+3z+9=0
27. a) -14 , 23 , 9 . . . . . b) (-10,2,8) , (-2,14,5) , (6,-8,-15) . . . .. c) -34
28.
. . . . . 29. 6x-y-5z+5=0
30. d(A,B)=4'123 , . . . d(A,C)=10'198 , . . . d(B,C)=8'307 . . . . . . 31. d(P,p)=3'838
32. d(P,p)=3'522 . . . . . 33. d(p,p')=0'730 . . . . . 34. d(P,r)=5'145
35. a) d(r,s)=4'920 ; . . . b) d(r,s)=3'567 . . . . . . 36. d(r,p)=4'082
37. A=60º . . . . . 38. A=13º13'8" . . . . . . 39. A=60º . . . . . 40. S=9'487
41. V=22/3=7'33 u3 . . . . . . 42.
. . . . . . 43. x-2z+3=0
44. a) P'(-2,3,2) ; . . . b) P'(22/7,-19/7,38/7) ; . . . c) P'(80/29,-11/29,56/29)
45. P(4/5,1/5,13/5) ; . . . Q(-1/10,1/5,23/10) . . . . d(r1, r2)=0'949
46. 4x-y+5z+7'114=0 . . . . . 47. D(0,3,4) ; . . . D(8,-5,-4) . . . . . . 48. S=2'446
49. A(19/8,17/16,-5/8) ; . . . B(3/10,-41/20,-27/10)
50. 2x-2y+z+10=0 ; 2x-2y+z-26=0 . . . 51. Los planos son: 
; 
52. 75/2=37'5 u3 . . . . . . 53. hD=0'742 u. . . . . . . . 54. P(2/3,0,2/3)
55. 2x+y-z+2'449=0 ; . . . 2x+y-z-2'449=0
56. ABCD: z=0, . . A'B'C'D': z=4'243, . . . AA'BB': x+y=3, . . . CC'DD': x+y=-3,
AA'DD': x-y=3, . . . BCB'C': x-y=-3. . . . . . ACB': 1'414y-z=0, . . . BDA': 1'414x-z=0
b) cosA=1/3 , A=70º31'43''
57. b) C(28/11, 29/11, -5/11) . . . . . c) D(99/55, 91/55, 23/55)
58. x+y+z-11=0 . . . . . . . 59. P=(0,7/5,24/5) ; . . . . . Q=(-18/7,-1/7,30/7)
60. d(r,s)=3'212 u. . . . . . 61. V=a3/6 u3.
62. a) No son incidentes. . . . b) El vector v es paralelo a los tres planos.
63. a) x-y-2z=0 . . . . . b) x-y-2z-6=0
64. i) Si a no es 1 ni -2: Los tres planos se cortan en un único punto
ii)Si a=1: Son coincidentes.
iii) Si a=-2 cada dos planos se cortan en una recta paralela al otro plano.
65. Forman un tetraedro de volumen 8/3. . . . . . . 66. Las rectas se cruzan.
67. t=2 .SABCD=SABD=0'866. . . . . . . 68. Plano 8x+10y-22z+33=0
69. Plano :2x+3y-5z=0 D(B,p) = 0'973. . . . . . 70. Plano x-y+z=0 . . . . . . 71. Plano 4x+3y-z-8=0
72. t=55/4 y el punto P(114/4, 149/4, 271/4) . . . . . . 73. r': x-5 = y-2 = z+1 .
74. Área del triángulo S=1'871 que no depende de donde se sitúe el tercer vértice C.
75. El plano es 2x+y-z-9=0 . . . . . 76. d(r,s)=5'612 u. . . . . 77. t=2, punto de corte P(1,2,-1).
78. Plano x-y-z+1=0. . . . . 79. Planos paralelos , d(p1, p2) = 1'633
80. No están alineados. a=4 y b=0 y el punto D(4,1,2). . . . . . 81. No existe el plano pedido.
82. No son coplanarios.V=2/3 u3. d(C,p)=1'414 u. . . . . . . . . 83. -x+y+z-2=0 . . . . . . . 84. a=1/2.
85. 
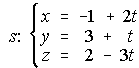. . . . . . . d(s,r)=3,8545
86. a)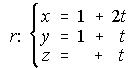
. . . . . . . . b) 2x+y+z=3 . . . . . . . . . c) (-1/3,1/3,-2/3)
87. a) Se cortan. . . . . . . . . . . . . . . . b) (-13,28,5)
88. a) a=6. Se cortan para cualquier valor de a. . . . . . . . . . . . . . b) (0,1,0)
c) (-4-2a)x-10y+(4a-2)z+10=0