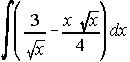 . . . . 2)
. . . . 2)-- INTEGRALES --
1. Calcula las siguientes primitivas:
1) 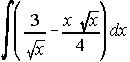 . . . . 2)
. . . . 2)![]() . . . . 3)
. . . . 3)![]() . . . . 4)
. . . . 4) ![]()
5)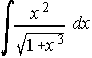 . . . . 6)
. . . . 6) ![]() . . . . 7)
. . . . 7)![]() . . . . 8)
. . . . 8) ![]()
9)![]() . . . . 10)
. . . . 10) ![]() . . . . 11)
. . . . 11)![]() . . . . 12)
. . . . 12) ![]()
13) ![]() . . . . 14)
. . . . 14) ![]() . . . . 15)
. . . . 15) ![]()
16) ![]() . . . . 17)
. . . . 17)![]() . . . . 18)
. . . . 18) ![]()
19) 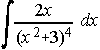 . . . . 20)
. . . . 20)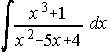 . . . . 21)
. . . . 21) ![]()
22) 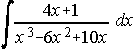 . . . . 23)
. . . . 23)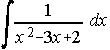 . . . . 24)
. . . . 24) 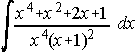
25) 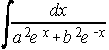 . . . . 26)
. . . . 26) 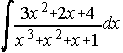 . . . . 27)
. . . . 27)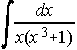 . . . . 28)
. . . . 28) 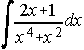
29)![]() . . . . 30)
. . . . 30)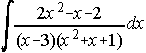 . . . . 31)
. . . . 31) ![]()
32)![]() . . . . 33)
. . . . 33)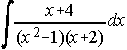 . . . . 34)
. . . . 34)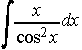
35)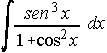 . . . . 36)
. . . . 36)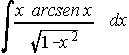 . . . . 37)
. . . . 37) ![]()
38)![]() . . . . 39)
. . . . 39)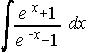 . . . . 40)
. . . . 40) 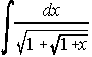
41)  (Prop 2.001) . .
(Prop 2.001) . .
2. Calcula las siguientes integrales:
a)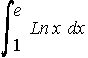 . . . b)
. . . b)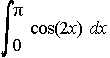 . . . c)
. . . c)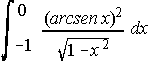 . . . d)
. . . d)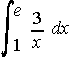
e)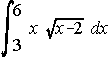 . . . f)
. . . f)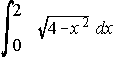 . . . g)
. . . g)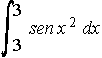 . . . h)
. . . h)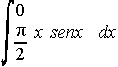
3. Aplica el teorema del valor medio del cálculo integral a las siguientes funciones en los intervalos que se indican:
a) f(x)= x2 en [0,1] . . . b) f(x)= a + bcosx en [-pi,pi] . . . c) f(x)= sen2x en [0,pi]
4. Halla f(0) y f'(0) sabiendo que f es continua y que:
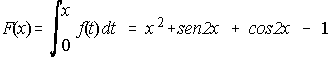
5. Sea la función F definida en (-1,1). Prueba que F alcanza un mínimo absoluto en este intervalo. Calcula su valor.
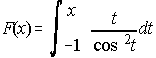
6. Dibuja la región del plano limitada por las curvas y=x2 ; y=2-x2 ; y=4. Calcula su área.
(Junio 94)
7. Calcula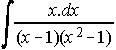 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (Junio 94)
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (Junio 94)
8. Calcula el área encerrada por las curvas y= x2 - 2x - 5 ; x + y =1.
9. Calcula el área limitada por el eje de abcisas y la gráfica de la función: f(x)=-x3 + 3x2 + x -3.
10. Determina "a y b" para que la función f(x) sea continua y después calcula la integral definida de f(x) entre -2 y 2.
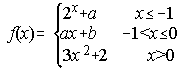
11. Deduce la fórmula del área del circulo de radio R.
12. Deduce la fórmula del volumen de una esfera de radio R.
13. Deduce la fórmula del volumen de un cono de altura h y radio r.
14. Calcula el volumen del cuerpo de revolución engendrado por el arco de curva y= 2senx + 1, en [0,pi] al girar entorno al eje X.
15. Esboza la gráfica de la función f(x) y obtén el volumen del sólido de revolución engendrado al girar, alrededor del eje OX, la región limitada por el semieje de abscisas negativas y la gráfica de la función.
![]()
16. Calcula el volumen del sólido engendrado al girar en torno al eje OX la curva f(x)= cos2x para x comprendido entre 0 y pi.
17. Calcula el área encerrada entre las curvas de ecuaciones y= x-1; y= x2 - 2x + 1.
18. Determina el área de la región del plano delimitada por:
a) f(x)= x2 - 5x + 4 y las rectas x + 5 = 0 y x - 5 = 0.
b) El eje OX, la gráfica de la función f(x)=x3 - x y las rectas de ecuaciones x+2=0 y x - 3 = 0.
c) La parábola y= x2 y la función y= x3. . . . . . . d) La parábola x = 4y2 y la recta x + y = 0.
19. Calcula la función primitiva de la función f(x) que pasa por el punto(2,(ln4)/3).
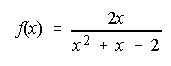
20. Halla el área comprendida entre la curva y=Ln(x+5) y las rectas y=0; x=-9/2 ; x=1.
Universidad de Córdoba
21. Dada la función f(x) de [0,3] a R, comprueba la verificación del teorema del valor medio del cálculo integral.
![]() Universidad de Santiago
Universidad de Santiago
22. Determina el área acotada por f(x)=x2.Ln x , su tangente en el punto de abscisa x=e y el eje OX. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Universidad de Madrid
23. Calcula la integral: . . . . . . . . . . . . . . . . . . . . . . . . Universidad de Valencia
. . . . . . . . . . . . . . . . . . . . . . . . Universidad de Valencia
24. Calcula el área limitada por la circunferencia x2+y2=1, y las rectas y=0 y x=1/2 en el primer cuadrante. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Universidad Autónoma de Madrid
25. Calcula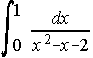 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Universidad Autónoma de Madrid
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Universidad Autónoma de Madrid
26. Calcula el área de la región limitada por el eje de abscisas y la gráfica de la función f:[0,pi] a R definida por f(x)=ex.sen x . . . . . . . . . . . . . . . . . . . . . . . . . Universidad Autónoma de Madrid
27. Calcula el área acotada entre las curvas y=x(x-2) e y=x+4 . . Universidad Autónoma de Madrid
28. Calcula![]() . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Universidad Autónoma de Madrid
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Universidad Autónoma de Madrid
29. Calcula el volumen del cuerpo de revolución engendrado al girar alrededor del eje de abscisas
la región ![]()
30. Calcula el volumen del sólido encerrado por la circunferencia x2+(y-3)2=1 al girar alrededor del eje de abscisas. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Junio-86
31. Halla el conjunto de las primitivas de la función. Dichas primitivas, żestán definidas en x=2?
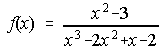 Junio-88
Junio-88
32. Calcula el área de la figura plana limitada por las gráficas de y=x2/2-x+1; y=x+1. . Junio-89
33. Representa gráficamente y=6x-x2 e y=2x; y determina el área limitada por ambas . . Junio-89
34. Calcula 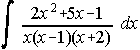
35. Calcula la integral de x2.sen 2x . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Septiembre-89
36. a) Enuncia el Teorema Fundamental del Cálculo Integral.
b) Calcula el área encerrada por la gráfica de: y=1/(4+x2) el eje de abscisas y las rectas x=2 y x=3.4641. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Junio-90
37. Resuelve la integral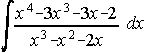 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Junio-90
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Junio-90
38. Calcula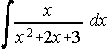 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Junio-91
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Junio-91
39. Interpretación geométrica del Teorema de la Media del Cálculo Integral. . . . . . . . . . . Junio-91
40. Calcula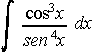 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Septiembre-91
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Septiembre-91
41. Calcula el volumen del cuerpo engendrado al girar alrededor del eje OX el recinto limitado por las gráficas de y=6x-x2 ; y=x. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Junio-92
42. Calcula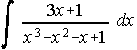 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Junio-92
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Junio-92
43. Dibuja el recinto limitado por las gráficas de y=2x ; y=x2-8. Calcula el área de dicho recinto.
Septiembre-92
44. Calcula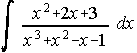 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Septiembre-92
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Septiembre-92
45. Calcula el volumen engendrado al girar alrededor del eje OX el recinto limitado por las gráficas de y=2x-x2 ; y=-x+2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Junio-93
46. Calcula la integral de cos x.cotag2x . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Junio-93
47. Dibuja la gráfica de f(x). Calcula 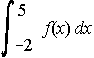 , siendo:
, siendo: 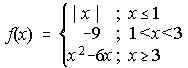
(Observa que f(x) está definida mediante "trozos" de funciones sencillas) . . . . . . . . . Septiembre-93
48. Calcula los valores "a, b y c" para que la función f(x)=ax2+bx+c verifica simultáneamente las condiciones:
a) f(2)=f(-2)=0 . . . . . . . . . . . . . . . . b) tiene un máximo relativo en x=0
c) el área de la región encerrada por la gráfica de la función y el eje OX es 32 unidades de área.
Septiembre-2.000
49. Halla el polinomio P(x) cuya derivada es 6x2 - 6x - 36 y que además P(x) alcance un máximo y un mínimo relativos tales que el valor máximo del polinomio sea el doble que el valor mínimo. Halla también esos valores máximo y mínimo. . . . . . . . . . . . . . . . . . . . . . . . . . . . Propuesto 2.001
50. Dibuja el recinto delimitado por las curvas y=-x2+2x+3 e y=|x+1|. Halla el área del recinto.
Propuesto 2.001
51. Dada la función y=xex y las rectas x=1 e y=0.
a) Dibuja la gráfica de la función para x>0 y la de las rectas.
b) Señala el recinto plano comprendido entre las tres gráficas anteriores.
c) Calcula el área del recinto plano señalado. . . . . . . . . . . . . . . . . . . . . . . . . . . . Propuesto 2.001
SOLUCIONES
1. 1.![]() . . . . 2. -ln|cosx| +k . . . . 3. tagx - x +k . . . . 4.
. . . . 2. -ln|cosx| +k . . . . 3. tagx - x +k . . . . 4. ![]()
5.![]() . . . . 6.
. . . . 6.![]() . . . . 7. ln|lnx| + k . . . . 8. x(lnx -1) + k
. . . . 7. ln|lnx| + k . . . . 8. x(lnx -1) + k
9.![]() . . . . 10.
. . . . 10.![]() . . . . 11.
. . . . 11. ![]()
12.![]() . . . . 13.
. . . . 13.![]() . . . . 14.
. . . . 14. ![]()
15.![]() . . . . 16.
. . . . 16.![]()
17.![]() . . . . 18.
. . . . 18.![]() . . . . 19.
. . . . 19. ![]()
20. ![]() . . . . 21.
. . . . 21. ![]()
22. ![]() . . . . 23.
. . . . 23. ![]()
24. ![]() . . . . 25.
. . . . 25.![]() . . . . 26.
. . . . 26. ![]()
27. ![]() . . . . 28.
. . . . 28.![]() . . 29.
. . 29. ![]()
30. ![]() . . . . 31.
. . . . 31. ![]()
32. ![]() . . . . 33.
. . . . 33.![]() . . . . 34.
. . . . 34. ![]()
35. cosx - 2 arctag(cosx) + k . . . . 36.![]() . . . . 37.
. . . . 37. ![]()
38.![]() . . . . 39. - ex - 2ln|1-ex| + k . . . . 40.
. . . . 39. - ex - 2ln|1-ex| + k . . . . 40. ![]()
41. ln|x| - arctg x + C . . .
2. a) 1 . . . . b) 0 . . . . c) pi3/24 . . . . d) 3 . . . . e) 326/15 . . . . f) pi . . . . g) 0 . . . . h) 1
3. a) c=0'5774 . . . b) c=±1'5708 . . . c) c=0'7854 . . . . 4. f(0)=2 y f'(0)=-2
5. Mínimo en (0,2'173) . . . . . 6. 8 . . . . . . 7.![]() . . . . . . . . 8. 125/6 . . . . . 9. 8
. . . . . . . . 8. 125/6 . . . . . 9. 8
10. a=3/4 y b=2. . . ![]() . . . . 14. 3pi2 + 8pi
. . . . 14. 3pi2 + 8pi
15. ![]() . . . . 16.
. . . . 16.![]() . . . . . . . 17. 1/6 . . . . 18. a)397/3 . . . b) 75/4 . . . c) 1/12 . . . d)1/96
. . . . . . . 17. 1/6 . . . . 18. a)397/3 . . . b) 75/4 . . . c) 1/12 . . . d)1/96
19.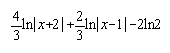 . . . . . . 20. 5'9 . . . . . .21. c=1'41 . . . . . . 22.
. . . . . . 20. 5'9 . . . . . .21. c=1'41 . . . . . . 22. ![]()
23.![]() . . . . . . . 24.
. . . . . . . 24.![]() . . . . . . 25.
. . . . . . 25. ![]() . . . . 26.
. . . . 26. ![]()
27. 125/6 . . . . . . 28.![]() . . . . . . . 29. 8pi2-2pi . . . . . . 30. 6pi2
. . . . . . . 29. 8pi2-2pi . . . . . . 30. 6pi2
31. ![]() . . . . . . 32. 16/3 . . . . . . . . 33. 32/3
. . . . . . 32. 16/3 . . . . . . . . 33. 32/3
34.![]() . . . . . . . . . . . . 35.
. . . . . . . . . . . . 35. ![]()
36. pi/24 . . . . . . . . . 37. ![]()
38. ![]() . . . . . . . 40.
. . . . . . . 40. ![]()
41. 625 pi/3 . . . . . 42. ![]()
43. 36 . . . . . . . . . 44.![]() . . . . . . . . 45. pi/5 . . . . . . . . 46.
. . . . . . . . 45. pi/5 . . . . . . . . 46. ![]()
47. -185/6 . . . . . . 48. a=-3 , b=0 , c=12
49. P(x)=2x3 - 3x2 - 36x + 206. Máximo (-2,250) Mínimo (3,125)
50. 9/2 u2. . . . . . . 51. 1 u2.