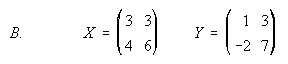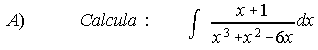
UNIVERSIDAD DE CASTILLA-LA MANCHA

Pruebas de aptitud para el acceso a la Universidad (BACHILLERATO L.O.G.S.E.)

MATERIA: MATEMÁTICAS II Esta prueba consta de cuatro bloques de dos preguntas cada uno. El alumno debe contestar solamente a dos de los bloques. Todas las preguntas puntúan igual (de cero a 2,5 puntos).

_______________________________________

PRIMER BLOQUE

A) El coste de producción de x unidades de un producto viene dado por la expresión

C=x²-300x+100 ptas. y el precio de venta de una unidad es U=1000-x ptas. ¿Cuántas unidades se deben vender para que el beneficio sea máximo?

B) Halla la distancia del punto P(2,4,1) al plano 3x+4y+12z-8=0, y encuentra el punto del plano que da la mínima distancia del punto P.

___________________________________________________________________________

SEGUNDO BLOQUE

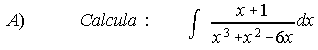
B) Estudia la compatibilidad del siguiente sistema de ecuaciones lineales según los diferentes valores del parámetro a, y resuelvelo cuando sea posible:

___________________________________________________________________________

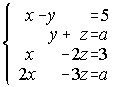
TERCER BLOQUE

A) Dada la función siguiente, determina a y b de modo que sea continua. Para los valores que se obtengan, estudia la derivabilidad

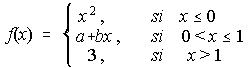
B) Halla el punto simétrico del punto A(1,2,3) respecto a la recta r.

___________________________________________________________________________

CUARTO BLOQUE

A) Calcula el área del recinto limitado por las curvas y=x²-1, y=11-x y el eje OX. Dibuja el recinto.

B) Resuelve el sistema de ecuaciones matriciales:

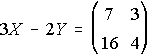
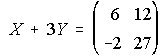
SOLUCIONES:

PRIMER BLOQUE:

A. 325 unidades

B. Distancia = 2 Punto = (20/13, 44/13, -11/13)

SEGUNDO BLOQUE:

A. -1/6 lnx- 2/15 ln x+3 + 3/10 ln x-2

B. a = 10; x=11, y=6, z=4

TERCER BLOQUE:

A. a=0 y b=3 No es derivable en x=0 ni en x=1

B. Punto = (7/3, 10/3, 5/3)

CUARTO BLOQUE:

A. 116/3 u²