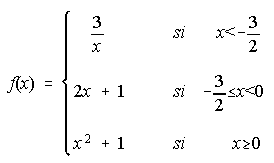
UNIVERSIDAD DE CASTILLA-LA MANCHA

Pruebas de aptitud para acceso a la Universidad (Bachillerato L.O.G.S.E.)

Materia: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II

Esta prueba consta de cuatro bloques de dos ejercicios A) y B) cada uno. El/la alumnos/a debe resolver cuatro ejercicios, uno de cada bloque. Cada ejercicio tiene una puntuación máxima de 2,5 puntos. Se puede utilizar cualquier tipo de calculadora.

BLOQUE 1

A) Dada la función f(x)=2x³+3x²-12x+4. Se pide:

i) Pendiente de la recta tangente a la gráfica de la función en el punto de abcisa x=2.

ii) Escribir los intervalos, en donde la función sea creciente y en donde sea decreciente.

iii) Determinar los valores x en los que la función f alcanza un máximo relativo y un mínimo relativo, respectivamente ¿Cuánto vale la función f en esos puntos?.

B) Dada la función , se pide:

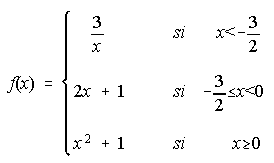
i) Estudiar la continuidad de f. ii) Representación gráfica de f.

iii) Área del recinto limitado por la gráfica de f, el eje 0X y la recta x=3.

BLOQUE 2

A) Dadas las matrices:

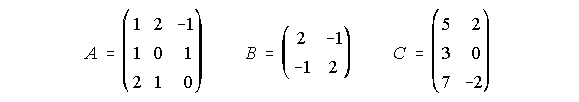
Se pide: i) Calcular la matriz inversa de A y la matriz inversa de B.

ii) Hallar una matriz X tal que A.X.B = C

B) En la lista de precios de una cafetería figura la siguiente información: Cuatro cafés y un bocadillo, cuestan lo mismo que cinco refrescos. Cuatro cafés y tres bocadillos, cuestan lo mismo que diez refrescos. Dos cafés, un refresco y un bocadillo cuestan 950 ptas. Calcular el precio de un café, de un refresco y de un bocadillo.

BLOQUE 3

A) Las 18 chicas y los 24 chicos de Bachillerato de una centro docente organizan un viaje. Para financiarlo deciden trabajar por las tardes en una empresa encuestadora que contrata equipos de dos tipos: Tipo A: Dos chicas y cuatro chicos. Tipo B: Tres chicas y tres chicos.

La empresa abona por una tarde de trabajo 3.000 ptas al equipo del tipo A y 5.000 ptas al equipo del tipo B. Se pide: i) Dibujar la región factible.

ii) ¿Cómo conviene distribuirse para obtener la mayor cantidad posible de dinero?

iii) Si la empresa abonara por una tarde de trabajo 4.000 ptas al equipo del tipo A y 5.000 ptas al equipo del tipo B. ¿Cómo les convendría hacer la distribución?

B) En un experimento aleatorio, la probabilidad de un suceso A es dos veces la probabilidad de otro suceso B y la suma de la probabilidad de A y la probabilidad del suceso contrario de B es 1,3. Se sabe, además, que la probabilidad de la intersección de A y B es 0,18. Calcular la probabilidad de que: i) Se verifique el suceso A o se verifique el suceso B.

ii) Se verifique el suceso contrario de A o se verifique el suceso contrario de B.

iii) ¿Son independientes los sucesos A y B?

BLOQUE 4

A) Se dispone de tres monedas. La 1ª de ellas está trucada de forma que la probabilidad de obtener cara es 0,4. La 2ª moneda tiene dos cruces y la 3ª moneda también está trucada de modo que la probabilidad de obtener cara es 0,6. Se pide:

i) escribir el espacio muestral correspondiente al lanzamiento de estas tres monedas, sucesivamente, y en el orden indicado.

ii) Probabilidad de que se obtengan, exactamente, 2 cruces.

iii) Probabilidad del suceso A="(cara, cruz,cara)".

iv) Probabilidad de obtener, al menos, una cara.

B) Queremos estimar la media de una variable aleatoria que se distribuye normalmente don una desviación típica de 3,2. Para ello, se toma una muestra de 64 individuos obteniéndose una media de 32,5. ¿Con qué nivel de confianza se puede afirmar que la media de la población está entre 31,5 y 33,5?

Si la desviación típica de la población fuera 3. ¿Cuál es el tamaño mínimo que debería tener la muestra con la cual estimamos la media poblacional si queremos que el nivel de confianza sea del 99% y el error admisible no supere el valor de 0,75?