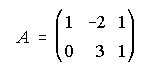 ,
,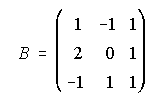 y
y 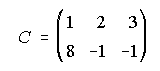
UNIVERSIDAD DE CASTILLA-LA MANCHA
Pruebas de aptitud para acceso a la Universidad (Bachillerato L.O.G.S.E.)
Materia: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II
Esta prueba consta de cuatro bloques de dos ejercicios A) y B) cada uno.
El/la alumnos/a debe resolver cuatro ejercicios, uno de cada bloque. Cada ejercicio tiene una puntuación máxima de 2,5 puntos. Se puede utilizar cualquier tipo de calculadora.
BLOQUE 1
A) Determina una matriz X tal que A+2.X.B=C,
siendo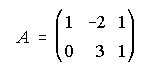 ,
,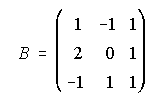 y
y 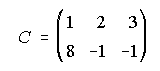
B) En una competición deportiva celebrada en un I.E.S. participaron 50 atletas distribuidos, según la edad, en tres categorías: Infantiles, Cadetes y Juveniles. El doble del número de atletas infantiles, por una parte excede en una unidad al número de atletas cadetes y, por otra parte, coincide con el quíntuplo del número de atletas juveniles. Determina el número de atletas que hubo en cada categoría.
BLOQUE 2
A) Se dispones de un dado trucado de cuatro caras con puntuaciones: 1, 2, 3 y 4, de modo que p(4)=4p(1), p(3)=3p(1), p(2)=2p(1) en donde p(4) indica la probabilidad de obtener la puntuación 4 y así sucesivamente. Se dispone también de dos urnas con la siguiente composición: Urna U1: 1 bola roja y 2 bolas verdes. Urna U2: 2 bolas rojas y 3 bolas verdes. Se lanza el dado, si sale puntuación par extraemos una bola de la urna U1 y si sale impar de la urna U2. Se pide:
a) Determina la probabilidad de los sucesos elementales que se presentan al lanzar el dado de cuatro caras.
b) Se lanza el dado y a continuación se extrae una bola de la urna que corresponda, halla la probabilidad de que sea de color verde.
B) Una tienda de golosinas dispone de dos tipos de bolsas de cumpleaños con el siguiente contenido:
Tipo I: 2 chicles, 3 piruletas, 8 caramelos y 1 bolsa de patatas fritas.
Tipo II: 4 chicles, 4 piruletas, 5 caramelos y 2 bolsas de patatas fritas.
En un determinado día, el número de chicles de que dispone la tienda para el envasado de las bolsas no puede ser superior a 240 unidades y el número de piruletas no puede superar las 300 unidades. Además, por problemas de envases, el número de bolsas del Tipo II no puede ser superior a 40.
El beneficio por la venta es: de 150 ptas por cada bolsa del Tipo I y 225 por cada bolsa del Tipo II. Halla el número de bolsas de cada tipo que deberían venderse en ese día para que el beneficio obtenido sea el mayor posible.
BLOQUE 3
A) Halla un número "xy" tal que la suma de sus cifras sea 12 y de modo que la suma del cubo de la cifra de las decenas y del triple del cuadrado de la cifra de las unidades sea lo más pequeña posible.
B) Dada la función 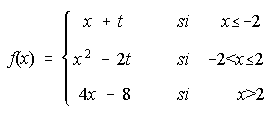 . Se pide:
. Se pide:
a) Halla el valor de "t" para que la función sea continua en todos los números reales.
b) Para el valor de "t" obtenido en el apartado anterior, representa gráficamente la función f(x).
c) Para el valor de "t" obtenido en el apartado a) calcula el área del recinto cerrado limitado por la gráfica de f(x) y el eje OX.
BLOQUE 4
A) Un estuche contiene 5 lápices de igual forma y tamaño: 2 de color azul y 3 de color verde. Se extrae un lápiz del estuche y a continuación, sin reemplazamiento, se extrae otro lápiz. Se pide:
a) Escribir los sucesos elementales que definen los suceson M="Sólo ha salido un lápiz de colro verde" y N="El segundo lápiz extraído es de color azul".
b) Calcula las probabilidades de los sucesos M, N y MN.
c) Estudia la independencia de los sucesos M y N. Razona la respuesta.
B) Según un estudio realizado por una empresa hostelera durante el año 1.992, la distribución del tiempo de estancia de cada viajero fue normal con una media de 3.7 días y una desviación típica de 1.1 días. A lo largo del año 2.000 se analizó el tiempo de estancia de 49 viajeros elegidos al azar, obteniéndose una media de 3.5 días. ┐Podemos afirmar que esta diferencia es debida al azar con una confianza del 88%? Con el mismo nivel de confianza, ┐cambiaría la respuesta si esta media de 3.5 días se hubiera obtenido al analizar el tiempo de estancia de 100 viajeros elegidos al azar?
SOLUCIONES:
BLOQUE 1:
A) 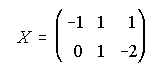
B) Hubo 15 atletas Infantiles, 29 Cadetes y 6 Juveniles
BLOQUE 2:A) a) p(1)=1/10 ; p(2)=1/5 ; p(3)=3/10 y p(4) 2/5 . . . . . . b) 16/25
B) 60 bolsas del Tipo I y 30 bolsas de Tipo II
BLOQUE 3:
A) El número es el 48
B) a) t=2 . . . . . . . c) 32/3 u2
BLOQUE 4:
A) a) M={AV, VA} ; N={AA, VA} . . . . . . b) P(M)=3/5 ; P(N)=2/5 ; P(MN)=3/10
c) No son independientes
B) Si podemos afirmar que se debe al azar. . . . . . . . Si cambiaría la respuesta.