UNIVERSIDAD DE CASTILLA-LA MANCHA
Pruebas de aptitud para acceso a la Universidad (Bachillerato L.O.G.S.E.)
Materia: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II
Esta prueba consta de cuatro bloques de dos ejercicios A) y B) cada uno. El/la alumnos/a debe resolver cuatro ejercicios, uno de cada bloque. Cada ejercicio tiene una puntuación máxima de 2,5 puntos. Se puede utilizar cualquier tipo de calculadora.
BLOQUE 1
A) Dada la ecuación matricial A.X+B=C, se pide obtener la martiz X siendo:
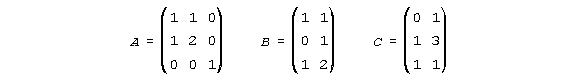
B) Entre Carlos, Raúl y Pedro suman 515 libros de distintos géneros literarios. Si el número de libros que posee Carlos le sumamos el triple de la diferencia entre los que tienen Pedro y Raúl, entonces Carlos tendría tantos como Raúl. Además 8 veces el número de volúmenes de Pedro equivale a 9 veces el número de los de Carlos. ┐Cuántos libros tiene cada uno?
BLOQUE 2
A) Una empresa fabrica dos tipos de videoconsolas M1 y M2, y dispone de dos naves en las que se efectúan, respectivamente, tareas de soldadura y ensamblaje. La nave dedicada a soldadura dispone de 750 horas de trabajo, y se sabe que se emplean 3 horas para una videoconsola M1 y 5 horas en una del tipo M2. La nave destinada al montaje dispone de 3.000 horas y se necesitan 21 horas para el ensamblaje del modelo M1 y 10 para el modelo M2. La ganancia netas son de 6.000 pesetas para el modelo M1 y de 4.000 pesetas para el M2. ┐Cuántas unidades deben fabricarse de cada tipo para maximizar las ganancias de la empresa?
B) El estudio de una muestra aleatoria de 100 jóvenes que se presentan a una prueba para a una prueba para un puesto de trabajo, en el ayuntamiento de una gran ciudad, revela que la edad media es de 20.2 años. Sabiendo que la variable estudiada se distribuye normalmente en la población con desviación típica 10. ┐Podemos aceptar con un 95% de confianza el valor de 22 años como media de edad de todos los que concurren a la prueba? ┐Cuál debería ser el tamaño de la muestra para que el intervalo de confianza de la media muestral fuera 20.2▒1.78 con el mismo nivel de significación?
BLOQUE 3
A) Se quiere construir una ventana rectangular de 1 m2 de superficie. Esta ventana se va a rodear de un marco cuyo coste es de 500 pesetas por metro de altura de ventana y 320 pesetas por metro de anchura. ┐Cuáles deben ser las dimensiones de la ventana para que el marco resulte más económico?
B) Una empresa ha realizado un estudio acerca de costes de producción llegando a la conclusión de que producir x unidades de un objeto dado tiene expresado por: f(x)=0.25x2+25x+25. La venta de x unidades de ese producto proporciona unos ingresos dados por la expresión i(x)=(30+0.125x)x, siendo x el número de unidades producidas. Se pide:
i) Hallar el número de unidades que se deben producir para que los costes sean mínimos.
ii) Hallar la expresión de los beneficios obtenidos en función de x, suponiendo que se venden las x unidades producidas.
iii) Hallar el número de unidades que se deben producir y vender para obtener máximo beneficio.
BLOQUE 4
A) Un fabricante de juguetes electrónicos garantiza una duración media de 100 horas en sus productos. Para efectuar un control de calidad sobre un lote de juguetes de un mismo modelo recientemente fabricados, se estudia de una muestra de 36 juguetes, obteniéndose una media de 97 horas, (la variable estudiada se distribuye normalmente siendo la desviación típica de la población igual a 10). Con una confianza del 95% ┐Debemos rechazar la producción por no cumplir con la duración garantizada? ┐Debemos rechazar la producción si deseamos una confianza del 99%? ┐Y si la muestra que elegimos es de 50 juguetes y la confianza del 95%?
B) Una compañía tiene dos proveedores A y B que le suministran artículos en mal estado en los últimos envíos. Los datos del último pedido son:
| Buenos | Defectuosos | Total | |
| Proveedor A | 10 | 40 | 50 |
| Proveedor B | 20 | 130 | 150 |
| Total | 30 | 170 | 200 |
Calcular la probabilidad de que al elegir al azar un artículo:
i) Sea bueno
ii) Sea del proveedor A
iii) Sea del proveedor A sabiendo que es defectuoso
iv) Sea del proveedor A y sea bueno
v) Sea suministrado por A o sea defectuoso.