UNIVERSIDAD DE CASTILLA-LA MANCHA
Pruebas de aptitud para acceso a la Universidad (Bachillerato L.O.G.S.E.)
Materia: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II
Esta prueba consta de cuatro bloques de dos ejercicios A) y B) cada uno. El/la alumnos/a debe resolver cuatro ejercicios, uno de cada bloque. Cada ejercicio tiene una puntuación máxima de 2,5 puntos. Se puede utilizar cualquier tipo de calculadora.
BLOQUE 1
A) Los gastos diarios de tres estudiantes, Marta, Raúl y Pedro suman 1.545 pesetas. Si a lo que gasta Marta se le suma el triple de la diferencia entre los gastos de Raúl y Pedro obtendremos lo que gasta Pedro. Ocho veces la diferencia entre el gasto de Raúl y el de Marta es igual al gasto de Marta. Averiguar cuál es la cantidad que gasta cada uno.
B) Una fábrica decide distribuir sus excedentes en tres productos alimenticios A, B y C a cuatro países de África P1, P2, P3 y P4 según se describe en la matriz M1 (cantidades en toneladas). Esta fábrica ha recibido presupuestos de dos empresas para el transporte de los productos a los países de destino como indica la matriz M2 (en euros por tonelada).
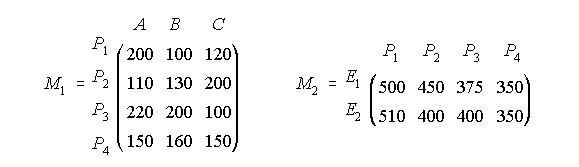
Efectúa el producto de las matrices y responde a las cuestiones:
i) ¿Qué representa el elemento a11 de la matriz producto?
ii) ¿Qué elemento de la matriz producto nos indica lo que cuesta transportar el producto C con la empresa E2?
iii) Indica que elementos de la matriz producto te permiten decir cuál es la empresa que más barato transporta el producto B a todos los países.
BLOQUE 2
A) En unos grandes almacenes se ha iniciado una campaña de venta de lavadoras y de televisores. Se ha calculado que un vendedor invierte 8 minutos en la venta de una lavadora y 10 en la venta de un televisor, mientras que un instalador dedica 12 minutos a una lavadora y 5 a un televisor. Se dispone de 4 vendedores y 3 instaladores cada uno de los cuales dedica 5 horas diarias a la venta o a la instalación de electrodomésticos durante los 16 días de campaña. sabe que se obtiene un beneficio de 45.000 pesetas por televisor y de 50.000 pesetas por la lavadora vendidos. ¿Cuántas lavadoras y televisores conviene poner a la venta para obtener máximos beneficios?
B) La probabilidad de que tenga lugar el contrario de un suceso es 1/3, la probabilidad de un suceso B es 3/4 y la probabilidad de que ocurran a la vez A y B es 5/8. Determinar:
i) Probabilidad de que se verifique el suceso A o el suceso B
ii) Probabilidad de que no se verifique el suceso A y no se verifique el suceso B
iii) Probabilidad de que ocurra A sabiendo que se ha verificado B
iv) Independencia de los sucesos A y B.
BLOQUE 3
A) Dada la función se pide:
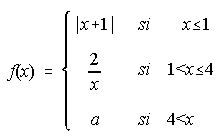
i) Gráfica de la misma ii) Estudiar su continuidad y hallar a para que sea continua en x=4.
iii) Determinar intervalos de crecimiento y decrecimiento
iv) Hallar la pendiente de la recta tangente a f(x) en x=3 y x=5.
B) Un publicista diseña un panel publicitario que tiene la siguiente forma: base horizontal de 10 metros de longitud y el resto limitado por la función siguiente:
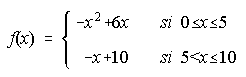
Se pide: i) Dibujar la gráfica del recinto correspondiente al cartel publicitario
ii) Calcular la superficie del mismo.
BLOQUE 4
A) Se tienen dos urnas U1 y U2 cuyo contenido en bolas rojas, azules y verdes es: en la urna U1 4 azules, 3 rojas y 3 verdes, en la urna U2 5 azules, 4 rojas y 1 verde. Se lanzan tres monedas y si se obtiene exactamente dos caras se extrae una bola de la urna U1, en otro caso se extrae de la urna U2. Se pide: i) Hacer un diagrama para el experimento aleatorio de lanzar tres monedas.
ii) Calcular la probabilidad de que la bola extraída sea azul.
B) El estudio de un test de satisfacción de usuario que rellenan todos los demandantes de servicios de una gran empresa revela que la nota media que otorgan es de 5.70 puntos con una desviación típica de 0.5. Posteriormente se ha realizado un muestreo a 100 usuarios de la zona de influencia A, y a 49 usuarios de la zona B, obteniéndose puntuaciones medias respectivas de 5.6 y 5.85. Con una confianza del 95%. ¿Se puede afirmar que las diferencias entre las medias de cada muestra y de la población son debidas al azar, o se puede afirmar que son diferentes la nota media de la población y la de cada muestra? Formula la hipótesis nula y alternativa. Define el error tipo I y error tipo II.