UNIVERSIDAD DE CASTILLA-LA MANCHA

Pruebas de aptitud para acceso a la Universidad (Bachillerato L.O.G.S.E.)

Materia: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II

Esta prueba consta de cuatro bloques de dos ejercicios A) y B) cada uno. El/la alumnos/a debe resolver cuatro ejercicios, uno de cada bloque. Cada ejercicio tiene una puntuación máxima de 2,5 puntos. Se puede utilizar cualquier tipo de calculadora.

BLOQUE 1

A) Dadas las matrices C y D, se pide:

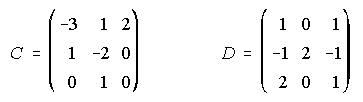
i) Calcula C^-1 y D^-1. ii) Calcula la matriz inversa de C.D.

iii)Comprueba que (C.D)^-1==D^-1.C^-1.

B) Una editorial va a lanzar al mercado tres libros de bolsillo L₁, L₂ y L₃. El importe total de la edición es 3.750.000 pesetas. Los costes en pesetas por unidad son 700, 500 y 600, respectivamente. Se sabe que el número de ejemplares de L₃ es igual a los dos séptimos de los del tipo L₂, y si al triple del número de ejemplares de L₁ se le suma el número de ejemplares de L₃ se obtiene el doble del número de ejemplares de L₂. Averigua cuántos libros se han editado de cada tipo.

BLOQUE 2

A) Una fábrica de adornos produce broches sencillos y broches de fiesta. Se obtiene un beneficio de 450 pesetas por cada broche sencillo y de 600 pesetas por cada broche de fiesta. En un día no se puede fabricar más de 400 broches sencillos ni más de 300 de fiesta y tampoco pueden producirse más de 500 broches en total. Suponiendo que se logra vender toda la producción de un día, ¿Cuál es el número de broches de cada clase que conviene fabricar para obtener el máximo beneficio? ¿Cuál debería ser la producción para obtener el máximo beneficio si se obtuvieran 600 pesetas por broche sencillo y 450 por el de fiesta?

B) Se extrae una carta de una baraja española de 40 cartas. Si la carta extraída es un rey nos dirigimos a la urna I, en caso contrario nos dirigimos a la urna II. A continuación sacamos una bola. EL contenido de la urna I es de 7 bolas blancas y 5 negras, el de la urna II es de 6 bolas blancas y 4 negras.

Halla la probabilidad de que la bola extraída sea:

i) Blanca y de la urna II. ii) Negra.

BLOQUE 3

A) Una persona amante de las Matemáticas desea donar sus 3.600 libros a dos bibliotecas A y B. Sus instrucciones son que los lotes de libros se hagan de manera que el producto del número de libros destinados a la biblioteca A por el cubo del número de libros destinados a la biblioteca B sea máximo. Determina la cantidad de libros recibida por cada biblioteca.

B) Dada la función siguiente, se pide:

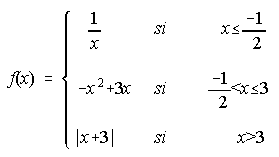
i) Gráfica de f(x). ii) Estudia la continuidad de f(x).

iii) Halla el área limitada por f(x), el eje OX y las rectas x=0 y x=3.

BLOQUE 4

A) En una ciudad el 55% de los habitantes consume pan integral, el 30% consume pan de multicereales y el 20% consume de ambos. Se pide:

i) Sabiendo que un habitante consume pan integral ¿Cuál es la probabilidad de que coma pan de multicereales?

ii) Sabiendo que un habitante consume pan de multicereales ¿Cuál es la probabilidad de que no consuma pan integral?

iii) ¿Cuál es la probabilidad de que una persona de esa ciudad no consuma de ninguno de los dos tipos de pan?

B) Se sabe que el contenido de fructosa de cierto alimento sigue una distribución normal cuya varianza es conocida teniendo un valor de 0.25. Se desea estimar el valor de la media poblacional mediante el valor de la media muestral de una muestra, admitiéndose un error máximo de 0.2 con una confianza del 95%. ¿Cuál ha de ser el tamaño de la muestra?