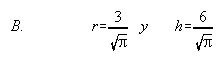UNIVERSIDAD DE CASTILLA-LA MANCHA

Pruebas de aptitud para el acceso a la Universidad (BACHILLERATO L.O.G.S.E.)

MATERIA: MATEMÁTICAS II Esta prueba consta de cuatro bloques de dos preguntas cada uno. El alumno debe contestar solamente a dos de los bloques. Todas las preguntas puntúan igual (de cero a 2,5 puntos).

---------------------------------------------

PRIMER BLOQUE

A) Halla la ecuación de la proyección ortogonal r' de la recta r sobre el plano x-3y+2z+12=0.

B) Calcula el área de la región del plano limitada por las gráficas de las funciones:

y=-x²+4x-4 e y=2x-7.

______________________________________________________________________________

SEGUNDO BLOQUE

A) Dados el punto P(2,1,2) y la recta r, determina la ecuación del plano que contiene a ambos.

.

______________________________________________________________________________

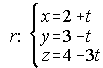
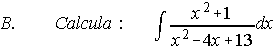TERCER BLOQUE

A) Estudia la continuidad y derivabilidad de la función:

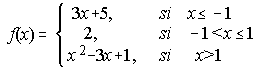
B) Dada la matriz A, halla los valores de x para los cuales la matriz no es inversible. Halla la inversa de A para x=2.

______________________________________________________________________________

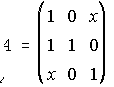
CUARTO BLOQUE

A) Dados los planos :x+y+z=1, :ax+y=1 y :x+(a+1)z=0, determina los valores de a para los cuales:

1) los planos se cortan en un sólo punto; 2) se cortan en una recta de puntos.

B) Se desea construir un depósito de latón con forma de cilindro de área total igual a 54 m². Determina el radio de la base y la altura del cilindro para que el volumen sea máximo.

SOLUCIONES:

PRIMER BLOQUE:

A. x=25t; y=4+23t; z=22t

B. 22/3 u²

SEGUNDO BLOQUE:

A. 2x-y+z-5=0

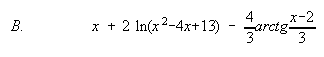
TERCER BLOQUE:

A. Continua en -{-1}. Derivable en -{±1}

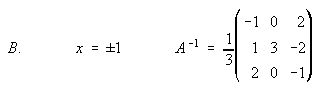
CUARTO BLOQUE:

A. Si a es distinto de 0 se cortan en un punto. Si a=0 se cortan en una recta.