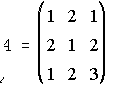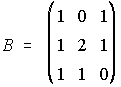
-- PROBLEMAS DE MATRICES --

1. Se consideran las matrices A y B. Calcula A+B, A-B, A·B, B·A, A², B², A³.

,

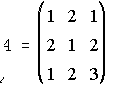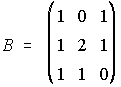
2. Calcula A²-3A-I, siendo A=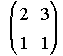 y I=.

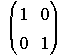3. Halla todas las matrices A que satisfacen la ecuación: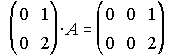

4. Se consideran las matrices A, B e I. a) Calcula B³. b) Calcula A³. (Sugerencia: A=B+I)

, ,

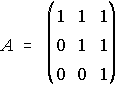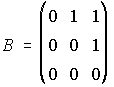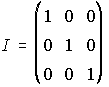
5. Dadas las matrices A, B y C. Calcula Aⁿ, Bⁿ, Cⁿ.

, , .

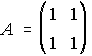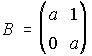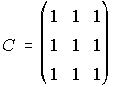6. Calcula Aⁿ siendo A=.

7. Calcula mediante la definición, la matriz inversa de las siguientes matrices:

, ,

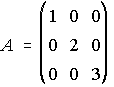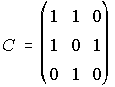
8. Demuestra que si A·B=A y B·A=B, entonces la matriz A cumple A²=A.

9. Demuestra que si A²=A y B=2A-I, entonces B²=I.

10. Estudia según los valores de t el rango de las siguientes matrices:

, ,

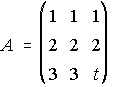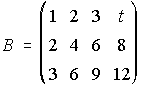11. Dada la matriz X=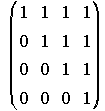, halla X² y X³.

12. Calcula los siguientes determinantes de orden 3:

13. Sabiendo que es 25, calcula el valor de .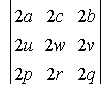

14. Demuestra, sin desarrollar que el determinante 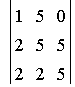es múltiplo de 15.

15. Demuestra, sin desarrollar que el determinante 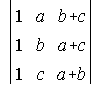vale 0.

16. Si 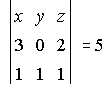, calcula, sin desarrollar, los siguientes determinantes:

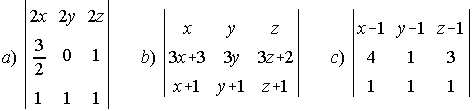
17. Sin desarrollar los determinantes, demuestra la identidad: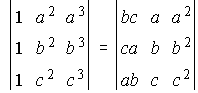

18. Calcula los siguientes determinantes:

19. Averigua, utilizando determinantes, si existe algún valor de m para el cual sean linealmente dependientes los vectores (2,1,3,1), (1,0,1,0) y (3,m,0,1).

20. Encuentra el valor de t que haga que los vectores u=(1,1,1), v=(2,2,t) y w=(1,3,-1) sean dependientes.

21. Comprueba que existe la inversa de la siguiente matriz cualquiera que sea el valor de a y calculala: .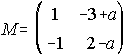

22. Dadas las matrices comprueba que det(A)·det(B)=det(A·B).

23. Dada la matriz A, se llaman "valores propios" de dicha matriz a los valores de "t", tales que el determinante de la matriz A-tI sea nulo. Halla los valores propios de A.

24. Siendo las matrices siguientes. Calcula A^-1·B·A.

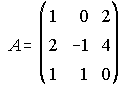y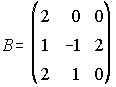

25. Estudia el rango de las siguientes matrices según los valores del parámetro t:

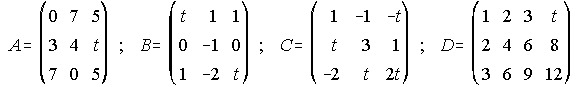
26. Calcula las matrices inversas de las siguientes matrices:

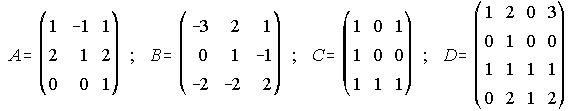
27. Calcula el rango de las siguientes matrices:

28. Calcula los siguientes determinantes de orden n:

29. Demostrar que si A y B son matrices cuadradas que tienen inversas, entonces:

(A·B)^-1 =B^-1·A^-1.

30. ¿Es cierto que det(A+B) = det(A) + det(B) ?, siendo A y B matrices cuadradas. Si es falso pon un contraejemplo.

31. Demuestra que toda matriz A que cumple A² + 2A = I tiene inversa.

32. Se da la matriz A. Comprueba que existe la matriz inversa de A y hallala. . . . . . . . . (Junio 88)

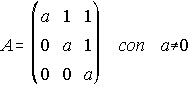
33. Define rango de una matriz. ¿Cuál es el mínimo rango que puede tener la siguiente matriz?

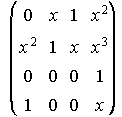(Junio 89)

34. Estudia del rango de la siguiente matriz según los valores del parámetro t.

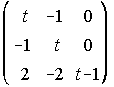(Junio 89)

35. Estudia el rango de la matriz según los valores del parámetro "t". ¿Para qué valores de "t" existe A^-1?. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (Septiembre 89)

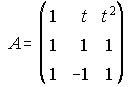
36. Define rango de una matriz. Muestra una matriz de orden 3 x 4 que tenga rango 2.

Calcula el rango de la matriz A, para los distintos valores de t

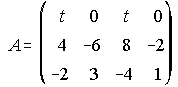(Junio 90)

37. a) Muestra con ejemplos las propiedades de los determinantes.

b) Halla una matriz X tal que: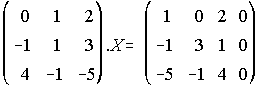 . . . . . . . . . . (Junio 90)

38. Dada la matriz A, averigua para qué valores de t no existe A^-1. Obtén A^-1 para t=1/2.

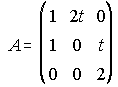(Septiembre 90)

39. Encuentra una matriz X que verifique la ecuación A·X + B = C, siendo:

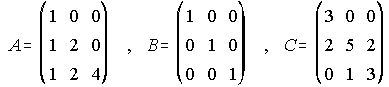(Junio 91)

40. Estudia el rango de la matriz A, para los diferentes valores de t. ¿Para qué valores de t existe A^-1? . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (Septiembre 91)

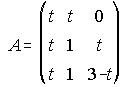
41. Calcula el rango de la matriz A según los diferentes valores de t, ¿Para qué valores de t, existe A^-1? . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (Junio 92)

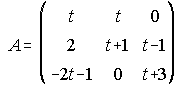
42. a) Define rango de una matriz. Escribe una matriz de orden 3x4 que tenga rango 2.

b) Halla la matriz X que cumple la ecuación: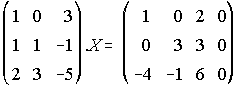

(Septiembre 93)

43. Sean las matrices A y B: a) Estudia, si existe, y, si es así, calcula la matriz inversa de A.

b) Determina una matriz X que verifique la ecuación A.B=A.X.A

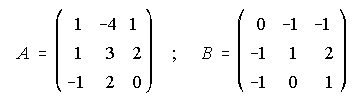
(Septiembre 2.000)

44. Dadas las matrices: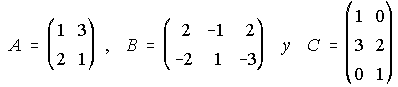

a) Halla la matriz inversa de 2A-BC. . . . . . . . b) Resuelve la ecuación matricial 2AX=BCX+A².

(Propuesto 2.001)

45. Dadas las matrices :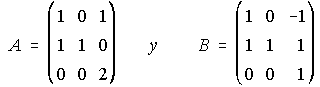

a) Halla paso a paso la de la matriz A.

b) Resuelve la siguiente ecuación matricial AX-B=A.B . . . . . . . . . . . . . . . . . . . . (Propuesto 2.001)

SOLUCIONES

1.

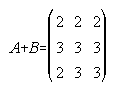
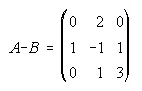
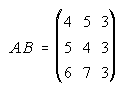
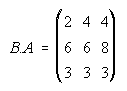
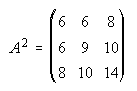
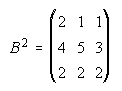
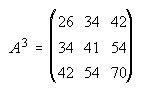
2. 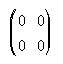. . . . . . . . .3. 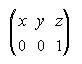. . . . . . . . . 4.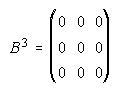

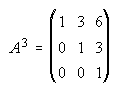
5.

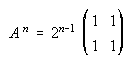
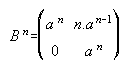
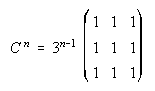
6. 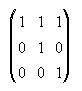. . . . .7.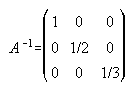

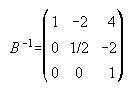
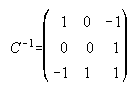
10. a) t=3 rg(A)=1 , t no es 3 rg(A)=2 . . . . . b) t=4 rg(B)=1 , t no es 4 rg(B)=2

c) t=1 rg(C)=2 , t=3 rg(C)=2 , t no es 1 ni 3 rg(C)=3

11.

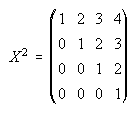
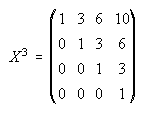
12. a)-15 . . . b)-36 . . . c)-11 . . . . d)0 . . . e)36 . . . f)11 . . . g)42 . . . h)32

13. 200 . . . . . . . . . . 16. a) 5 . . . . . b)5 . . . . . c)5 . . . .18. a)8 . . . b)(x+1)³ . . . c)-2 . . . . . d)-72

19. No . . . . . . . . . . . . . . . . 20. t=2

21. 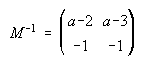. . . . . . . . 23. -1 y 4 . . . . . . . 24.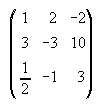

25. t no es 5 rg(A)=3; t=5 rg(A)=2 ; . . . . . t no es ±1 rg(B)=3; t=±1 rg(B)=2

t no es 2 rg(C)=3; t=2 rg(C)=2 ; . . . . . . . . . t no es 4 rg(D)=2; t=4 rg(D)=1

26. ,

,

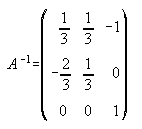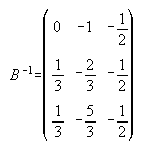
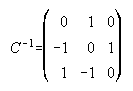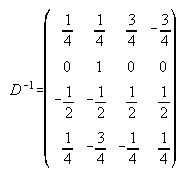
27. rg(A)=3; . . . rg(B)=3; . . . . rg(C)=2 . . . .. . . . 28. n! . . . . . n!

32. . . . . 33. Si x=1 o x=-1 rango=3 , si no es 4

34. Si t no es 1 ni -1 rg=3 ; Si t=1 rg=1; Si t=-1 rg=2.

35. Si t no es 1 ni -1 rg=3 ; Si t=1 rg=2 ; Si t=-1 rg=2. . . . Para t distinto de 1 y -1.

36. t=0 rg=1 ; Si t no es 0 rg=2.

37.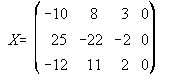 38. Para t=0. 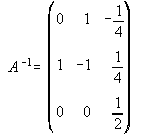39.

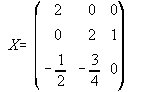
40. a)Para t distinto de 0, 1 y 3/2 rg(A)=3 y existe A^-1 ; . . . . . . . b) Si t=0 rg(A)=2 ;

c) Si t=1 rg(A)=2 ; . . . . . . . . . . . . . . d) Si t=3/2 rg(A)=2.

41. a)Para t distinto de 0, 1 y 2 rg(A)=3 y existe A^-1 ; . . . . . . . . . . b) Si t=0 rg(A)=2 ;

c) Si t=1 rg(A)=2 ; . . . . . . . . . . . . . . d) Si t=2 rg(A)=2.

42. 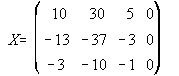43. a) 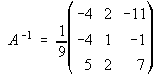. . . b)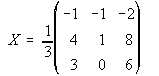

44.

45.