MATRICES

1. Resuelve la ecuación matricial siguiente e indica la dimensión de la matriz X:

2. En un centro de estudios de idiomas los alumnos de Francés y Alemán se distribuyen en 4 niveles como indica la matriz A. Los precios que pagan los alumnos por hora depende del nivel en que se encuentren y de que el aula disponga o no de puestos de laboratorio de idiomas, según figura en la matriz B. Calcula lo que percibirá este centro educativo por hora de cada idioma impartido dependiendo de que la aulas estén o no dotadas de los medios mencionados.

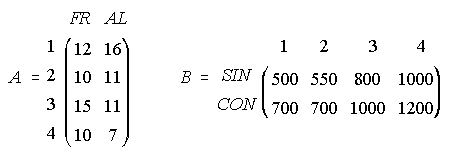
3. Una factoría produce encendedores P₁, rotuladores P₂ y llaveros P₃, para cuya elaboración se precisan materias primas como gas M₁, tinta M₂, plástico M₃ y metal M₄. Dos compañías distribuidoras D₁ y D₂ se encargan de proporcionara los comercios estos productos. Sea A la matriz de pedido de los tres productos por parte de los distribuidores, B la matriz que expresa la cantidad de cada una de las materias primas, en gramos, por unidad de cada producto y C la matriz de costes por gramo de cada material:

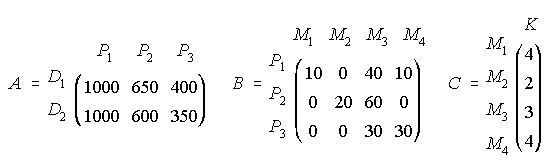
Responde: ¿Qué materias primas forman parte de los llaveros y en qué cantidades por unidad producida?

Calcula e interpreta el resultado de A.B; B.C ; A.B.C

4. Dada la ecuación A.X=C, halla la solución, si existe, y en caso de que no exista explica la causa, siendo:

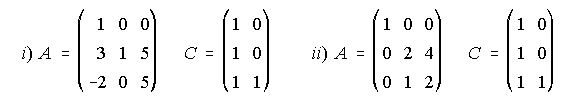
5. Una fábrica produce tres tipos de artículos A₁, A₂ y A₃, distribuyendo su producción entre cuatro clientes. En el mes de marzo el primer cliente ha adquirido 9 unidades de A₁, 5 de A₂ y 2 de A₃, el segundo cliente 3, 8 y 0 respectivamente, no compró nada el tercer cliente, y el cuarto 6, 7 y 1 unidades respectivamente. En abril el cuarto cliente no hizo pedido alguno, el tercer cliente compró 4 unidades de cada artículo, mientras que los otros dos duplicaron el número de unidades adquiridas en marzo.

i) Construye las matrices 4x3 correspondientes a las ventas de los meses de marzo y abril.

ii) Si los precios de los artículos son (en miles de pesetas por unidad) 10, 8 y 9 respectivamente, calcular lo que factura la fábrica a cada cliente por sus pedidos en los meses de marzo y abril.

6. En un centro educativo los datos de matrícula por cursos son: 3º de secundaria: 50 alumnos y 70 alumnas; 4º de secundaria 65 alumnos y 50 alumnas; 1º de bachillerato 35 alumnos y 38 alumnas; y en 2º de bachillerato 21 alumnos y 30 alumnas. Un estudio realizado en el centro indica que cada alumno/a de 3º lee por año 2 libros de novela, ninguno de poesía y 1 libro de otros temas; cada alumno/a de 4º lee 3 novelas, 1 de poesía y 2 de otros temas; un alumno/a de 1º lee sólo 4 novelas; y un alumno/a de 2º lee 4 novelas, 3 de poesía y 4 de otros temas.

Se pide: i) Disponer la información de matrícula y lectura en matrices. ii) ¿Qué representan los elementos de la matriz producto de las dos anteriores? iii) ¿Cuántos libros de novela leen por curso todas las alumnas matriculadas en el centro?

7. Una empresa de carpintería dispone de dos naves A y B donde se fabrican sillas y mesas en tres tipos de acabados: calidad extra E, calidad media M y calidad inferior I. Ambas naves tienen la misma producción mensual. La cantidad de sillas producidas mensualmente, en cada una de las naves, es de 100 del tipo E, 150 del M y 200 del I; la producción mensual de mesas es de 100 de clase E, 50 de clase M y 300 de clase I. Se sabe que el porcentaje de sillas y mesas defectuosas es, en la nave A, de 0.01 para los muebles de calidad E, de 0.02 para los de calidad M y 0.03 para los de calidad I, mientras que en la nave B los porcentajes son 0.02 para clase E, 0.04 para clase M y 0.01 para la I. Se pide:

i) Obtener la matriz que representa la producción de sillas y mesas, de calidad extra, media o inferior en una de las dos naves.

ii) Obtener la matriz que representa el número de sillas y mesas defectuosas, en las calidades E, M e I, procedentes de cada una de las naves y la matriz que da el número total de sillas y de mesas defectuosas para cada calidad. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (Septiembre-97)

8. Dada la ecuación matricial A.X+B=C, se pide obtener la matriz X siendo:

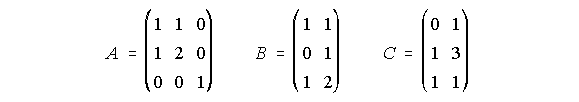
(Junio-97)

9. Dadas las matrices A, B y C:

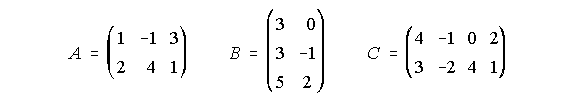
i) Halla A.B y B.A ¿Puedes sacar alguna conclusión de los resultados obtenidos?

ii) ¿Existe alguna matriz tal que multiplicada por C, de lugar a un matriz de 3 filas?

10. Resuelve la ecuación X.A+X=2B siendo:

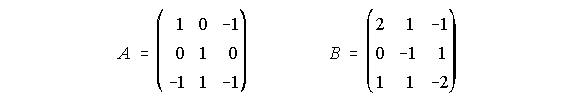
(Septiembre-98)

11. Una fábrica decide distribuir sus excedentes en tres productos alimenticios A, B y C a cuatro países de África P₁, P₂, P₃ y P₄ según se describe en la matriz M₁ (cantidades en toneladas). Esta fábrica ha recibido presupuestos de dos empresas para el transporte de los productos a los países de destino como indica la matriz M₂ (en euros por tonelada).

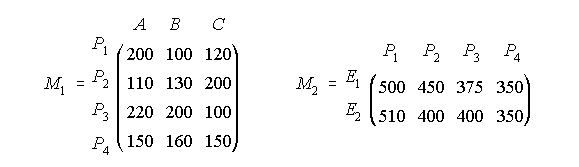
Efectúa el producto de las matrices y responde a las cuestiones:

i) ¿Qué representa el elemento a₁₁ de la matriz producto?

ii) ¿Qué elemento de la matriz producto nos indica lo que cuesta transportar el producto C con la empresa E₂?

iii) Indica que elementos de la matriz producto te permiten decir cuál es la empresa que más barato transporta el producto B a todos los países.

12. Dadas las matrices C y D se pide: i) Calcula C^-1 y D^-1.

ii) Calcula la matriz inversa de C.D. iii)Comprueba que (C.D)^-1=D^-1.C^-1.

. . . . . (Junio-99)

13. Los consumos de agua mineral, pan y leche de tres familias vienen expresados en la matriz A. La evolución de los precios de los años 1.995 a 1.998 viene reflejada en la matriz B.

i) Halla, si es posible, A.B y B.A e indica qué información proporciona el producto matricial.

ii) ¿Qué información nos da el elemento c₃₄ de la matriz producto?

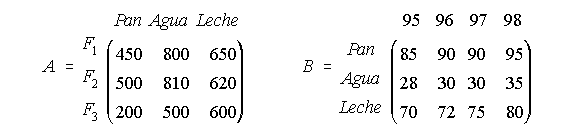
(Septiembre-99)

14. Dadas las matrices:

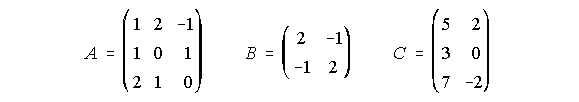
Se pide: i) Calcular la matriz inversa de A y la matriz inversa de B.

ii) Hallar una matriz X tal que A.X.B = C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (Junio-2.000)

15. Dadas las matrices siguientes se pide calcular una matriz X tal que se cumpla que:

X.A = 2.B + C:

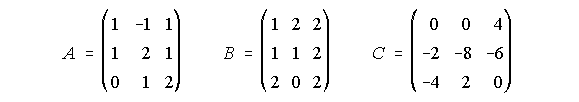
(Septiembre-2.000)

16. Dadas las matrices

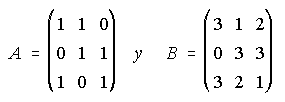
Se pide: i) Calcular la matriz inversa de A. ii) Hallar una matriz X tal que A.X+A = B

(Propuesto-2.000)

17. Una fábrica de calzado deportivo dispone de zapatillas para Atletismo (A), Balonmano (B) y Tenis (T), en dos modelos: Mujer (M) y Hombre (H). El número de pares existentes en el almacén viene definido por la matriz E. El precio, en Euros, de cada uno de los pares viene definido por la matriz P.

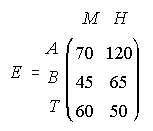
Se pide: i) Obtener, si es posible, las matrices C=P.E y D=E.P

ii) ¿Qué información proporcionan los elementos c₁₁ de C y d₃₃ de D?

iii) ¿Qué elemento de C o D nos informa de la valoración de todas las zapatillas de balonmano?

(Propuesto-2.000)

18. Determina una matriz X tal que A+2.X.B=C, siendo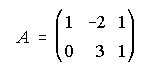, 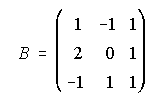y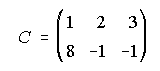 . (Junio-2.001)

19. Los precios, en euros, de las entradas a un parque temático para Adultos (AD) y Niños y Jubilados (NJ) en Temporada Alta (TA), Temporada Media (TM) y Temporada Baja (TB) vienen expresados en la matriz P. El número de asistentes, en miles, a dicho parque a lo largo de un año viene dado por la matriz N.

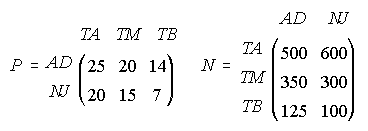. Se pide:

a) Obtener, si es posible, las matrices R₁=P.N y R₂=N.P

b) ¿A cuántos euros asciende la recaudación total correspondiente a los niños y jubilados? ¿Y la correspondiente a la Temporada Baja?

c) ¿Qué elemento de R₁ o R₂ nos proporciona información sobre la recaudación total correspondiente a los adultos?

d) ¿A cuántos euros asciende la recaudación total?

(Septiembre-2.001)

20. Dadas las matrices 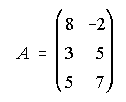, 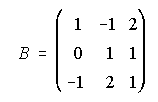y 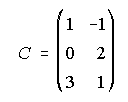, halla otra matriz X tal que A-BX=C.

(Propuesto-2.001)

21. En una tienda de discos se dispone de música Rap (R), Pop (P) y Folk (F) en dos formatos: Compact-Disc (CD) y Musicassette (MC). Los precios, en €, de los distintos ejemplares vienen determinados por la matriz D y el número de existencias de cada tipo de música y formato por la matriz E.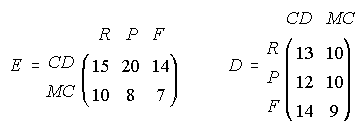. Se pide: a) Obtener, si es posible, las matrices V₁=D.E y V₂=E.D b) ¿A cuántos € asciende la valoración de las existencias de música Pop? ¿Y las de todos los CD? c) ¿Qué elemento de la matriz V₁ o V₂ nos proporciona información sobre la valoración de las existencias de música Folf? d) ¿A cuántos € asciende la valoración de las existencias de todos los tipos de música?

(Propuesto-2.001)

SOLUCIONES

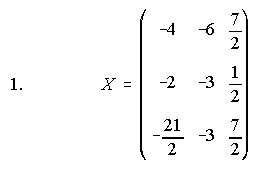
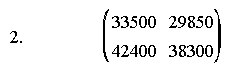
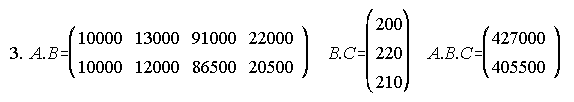
Los llaveros tienen plástico y metal, 30 gramos de cada.

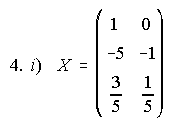
ii) La matriz A no se puede invertir.

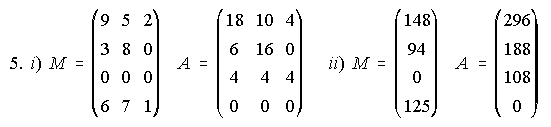
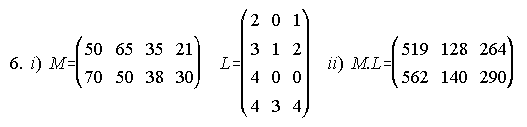
Los elementos de esta matriz representan el tipo de lectura según el sexo.

iii) 562 libros de novela leen las alumnas.

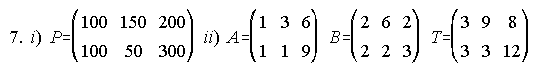
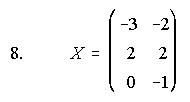
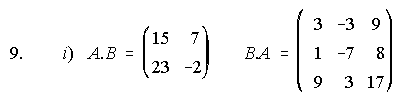
ii) Multiplicar por la izquierda con una 3x2.

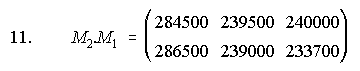
i) Lo que cuesta mandar los productos por la empresa E₁ al país A.

ii) El elemento a₂₃=233700

iii) Los elementos a₁₂ y a₂₂. El más barato es la empresa E₂.

12.

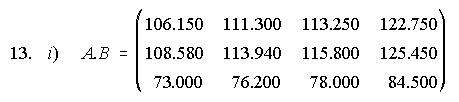
B.A no se puede hacer.

ii) El elemento c₃₄ indica lo que gasta F₃ en 1.998

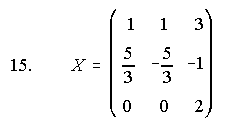
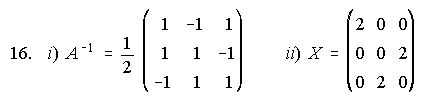
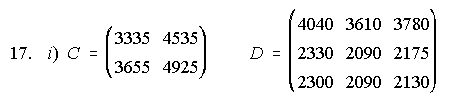
ii) El elemento c₁₁ nos indica el precio total de todas las zapatillas de mujer y el elemento d₃₃ nos indica el precio total de todas las zapatillas de tenis.

iii) El elemento d₂₂ nos indica el precio total de todas las zapatillas de balonmano.

18.

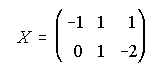
19. a)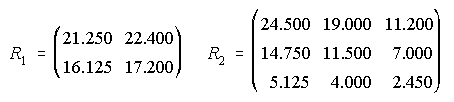

b) 22.400 €, 2.450 € . . . . . c)Elemento 11 de R₁. . . . . . . d) 38.450 €.

20.

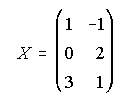
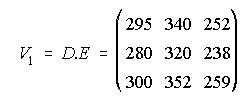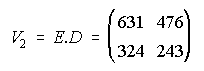21. y . . b) 320€; 631€ c)Elemento 33 de V₁. . . . . . . d) 874€