LAGRANGE Y CAUCHY--
1. Comprueba que la función f(x)= x3 - 4x2 +4x + 2 cumple el teorema de Rolle en [0,2] y halla los puntos c (0,2) tales que f'(c)=0.
2. Aplica si es posible el teorema de Rolle a la función f(x) en [-2,1] . . . . . . . (Septiembre 1991)
![]()
3. Estudia si la función f(x)= 4x-x2 cumple el teorema de Rolle en el intervalo [2,6].
(Junio 1992)
4. Calcula "a, b y c" para la función f(x) cumpla las hipótesis del teorema de Rolle en [-1,5].
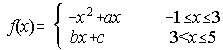
(Septiembre 1993)
5. Sea la función f(x), estudia si es posible aplicar el teorema de Lagrange a f(x) en [-2,3]. En caso afirmativo, encuentra los valores intermedios dados por el teorema.

(Septiembre 1989)
6. Sea la función f(x), determina "a y b" para que f(x) cumpla las hipótesis del Teorema de Lagrange en [2,6].
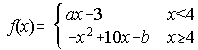
(Junio 1990)
7. Estudia si se puede aplicar el Teorema de Cauchy a las funciones f(x)= x2 -2x +3 y
g(x)= x3 -7x2 +20x -5 en [1,4]. En caso afirmativo, aplícalo. . . . . . . . . . . (Septiembre 1992)
8. Estudia si se cumple el teorema del valor medio y, en caso afirmativo, halla los puntos c cuya existencia asegura el teorema, en las funciones:
a)
f(x)= x(x-2) en [0,1] ; . . . . . . . . . . . . . . . b) g(x)= 2x+senx en [0,pi]9. a) Enuncia el teorema del valor medio de Lagrange.
b) Dada la función
f(x)=x3-3x2+5 ¿Podemos afirmar que la función toma el valor 1.4142 en algún punto del intervalo [1,2]? Razona la respuesta.SOLUCIONES
1. Si lo cumple y c=2/3 c pertenece al intervalo [0,2].
2. No es posible pues no es continua en x=0.
3. No pues no es derivable en x=4.
4. a=10/3, b=-8/3, c=9.
5. Si es posible y es c=13/20.
6. a=2, b=19.
7. Si se puede y es c=2.
8. a) Si y es c=1/2 ; b) Si y c=pi/2.