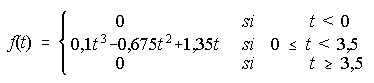
UNIVERSIDAD DE CASTILLA-LA MANCHA

Pruebas de aptitud para acceso a la Universidad (Bachillerato L.O.G.S.E.)

Materia: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II

Esta prueba consta de cuatro bloques de dos ejercicios A) y B) cada uno.El/la alumnos/a debe resolver cuatro ejercicios, uno de cada bloque. Cada ejercicio tiene una puntuación máxima de 2,5 puntos. Se puede utilizar cualquier tipo de calculadora.

BLOQUE 1

A) Una fábrica envasa al día durante una campaña de Navidad 180 kg. de turrón. Produce tabletas medianas y grandes de peso neto 200 gr. y 300 gr., respectivamente. Se deben fabricar un número de tabletas medianas no superior al triple de tabletas grandes. El beneficio es de 110 ptas. tableta mediana y 150 ptas por tableta grande. Se pide:

i) Representar la región factible.

ii) ¿Cuántas tabletas de cada clase deben producirse al día para que el beneficio sea máximo?

B) En un experimento aleatorio, se consideran dos sucesos A y B. La probabilidad de que no se verifique el suceso A es 0,1. La probabilidad de que no se verifique el suceso B es 0,4. La probabilidad de que no se verifique A ni B es 0,04. Hallar la probabilidad de que:

i) Se verifique el suceso A o se verifique el suceso B.

ii) Se verifique el suceso A y se verifique el suceso B. ¿Son independientes los sucesos A y B?

BLOQUE 2

A) El consumo de agua en un colegio viene dado por la función:

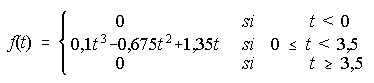
en donde t es el tiempo en horas a contar desde la apertura del colegio y f(t) es el consumo en m³. Se supone que la jornada escolar comienza a las 10 horas y termina a las 13,5 horas. Se pide:

i) ¿Cuándo el consumo de agua es creciente? ¿Cuándo el consumo de agua es decreciente?

ii) ¿En qué momento el consumo de agua es máximo y en qué momento es mínimo?

B) Dada la función

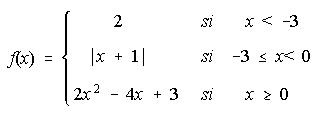
Se pide:

i) Estudiar la continuidad de la función. ii) Representación gráfica de f.

iii) Calcular el área del recinto plano limitado por la gráfica de f, el eje 0X, el eje OY y la recta x=3.

BLOQUE 3

A) Dadas las matrices siguientes se pide calcular una matriz X tal que se cumpla que:

X.A = 2.B + C:

B) Los 345 atletas que llegaron a la meta en una prueba de maratón se pueden agrupar así: Grupo A: Atletas cuyo tiempo final está comprendido entre 2 y 3 horas. Grupo B: Atletas cuyo tiempo final está comprendido entre 3 y 4 horas. Grupo C: Atletas cuyo tiempo está comprendido entre 4 y 5 horas. El número de atletas del grupo A excede en 4 unidades al triple del número de atletas del grupo C. La diferencia entre el número de atletas del grupo B y el número de atletas del grupo A es cuatro veces el número de atletas del grupo C disminuido en 4 unidades. Calcular el número de atletas que hay en cada grupo.

BLOQUE 4

A) Una caja tiene 7 tarjetas de la misma forma y tamaño: 4 de color amarillo y 3 de color rojo. Se extrae de ella una tarjeta, se anota su color y sin devolverla a la caja extraemos una segunda tarjeta. Se pide:

i) Escribir el espacio muestral.

ii) Hallar la probabilidad de cada uno de los sucesos elementales del espacio muestral.

B) Según un estudio realizado durante el año 1.999 en un hospital, la distribución de los pesos de los recién nacidos fue una Normal con media 3,450 Kg. y desviación típica 0,52 Kg. A lo largo de este año se ha analizado el peso de 36 recién nacidos tomados al azar, obteniéndose una media de 3,300 Kg. ¿Podemos afirmar que esta diferencia es debida al azar con una confianza del 95%? Con el mismo nivel de confianza, ¿cambiaría la respuesta si la media de 3,300 Kg se hubiera obtenido al analizar el peso de 81 recién nacidos tomados al azar?