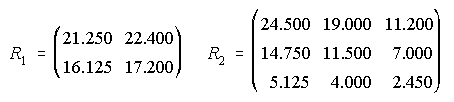UNIVERSIDAD DE CASTILLA-LA MANCHA
Pruebas de aptitud para acceso a la Universidad (Bachillerato L.O.G.S.E.)
Materia: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOLCIALES II
Esta prueba consta de cuatro bloques de dos ejercicios A) y B) cada uno.
El/la alumnos/a debe resolver cuatro ejercicios, uno de cada bloque. Cada
ejercicio tiene una puntuación máxima de 2,5 puntos. Se puede utilizar cualquier
tipo de calculadora.
BLOQUE 1
A) Se dispone de dos urnas iguales con el siguiente contenido: Urna P: 4 bolas amarillas y 6
granates. Urna Q: 5 bolas amarillas y 7 granates. Se dispone de un dado cúbico con las siguientes
puntuaciones: 1, 1, 2, 2, 2, 3. Se lanza el dado. Si sale el número 1 se extrae una bola de la urna P.
En los demás casos la bola se extrae en la urna Q. Se pide la probabilidad de que: a) Al lanzar el
dado se obtenga una puntuación mayor de 1. b) Al tomar una bola de la urna P sea de color
granate. c) Al extraer una bola, después de lanzar el dado, se obtenga de color amarillo.
B) Un Ciber-Café realiza dos ofertas entre sus clientes habituales:
Oferta I: 1 refresco, 3 bizcochos y 20 minutos de conexión a Internet.
Oferta I: 1 refresco, 2 bizcochos y 30 minutos de conexión a Internet.
Las características del local limitan a 50 horas diarias el tiempo máximo de conexión a Internet. Al
no disponer de almacén, sólo se puede acumular un máximo de 100 refrescos y 240 bizcochos. Un
cliente que opte por la Oferta I produce un beneficio de 500 ptas y si opta por la Oferta II, el
beneficio es de 450 ptas. Halla el número de clientes que deberían elegir cada una de las ofertas
para que el beneficio total fuese lo mayor posible.
BLOQUE 2
A) Los precios, en euros, de las entradas a un parque temático para Adultos (AD) y Niños y
Jubilados (NJ) en Temporada Alta (TA), Temporada Media (TM) y Temporada Baja (TB) vienen
expresados en la matriz P. El número de asistentes, en miles, a dicho parque a lo largo de un año
viene dado por la matriz N.
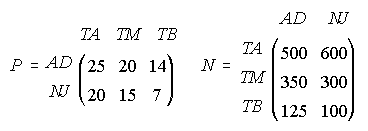 . Se pide: (a) Obtener, si es posible,
las matrices R1=P.N y R2=N.P (b) ¿A cuántos euros asciende la recaudación total correspondiente
a los niños y jubilados? ¿Y la correspondiente a la Temporada Baja? (c)¿Qué elemento de R1 o R2
nos proporciona información sobre la recaudación total correspondiente a los adultos? (d) ¿A
cuántos euros asciende la recaudación total?
. Se pide: (a) Obtener, si es posible,
las matrices R1=P.N y R2=N.P (b) ¿A cuántos euros asciende la recaudación total correspondiente
a los niños y jubilados? ¿Y la correspondiente a la Temporada Baja? (c)¿Qué elemento de R1 o R2
nos proporciona información sobre la recaudación total correspondiente a los adultos? (d) ¿A
cuántos euros asciende la recaudación total?
B) Dividimos un número de tres cifras, "xyz", entre la suma de estas y obtenemos 20 de cociente y
3 de resto. La cifra de las decenas, "y", es igual a la mitad de la suma de las otras dos. La cifra de
las unidades, "z", es igual a la suma de las otras dos. Halla el número "xyz".
BLOQUE 3:
A) El precio, en pesetas, que la acción de una empresa alcanza en el transcurso de una sesión de
Bolsa, viene dado por la función
p(t)=40t3-420t2+1200t+200, en donde t es el tiempo en
horas a contar desde el inicio de la sesión. Supongamos que la sesión comienza a las 10 de la
mañana y finaliza a las 7 horas de la tarde. Se pide: (a) ¿Entre qué horas el precio de la acción
sube? (b) ¿Entre qué horas el precio de la acción baja? (c)¿A qué hora el precio de la acción
alcanza un máximo relativo? ¿Cuál es este valor? (d) ¿A qué hora el precio de la acción alcanza un
valor mínimo relativo? ¿Cuál es este valor? (e) ¿A qué hora el precio de la acción alcanza su valor
más grande? ¿Cuál es este valor?
B) Dada la función 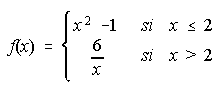 . Se pide:
. Se pide:
a) Estudiar la continuidad de f.
b) Representación gráfica de f.
c) Área del recinto cerrado que delimita la gráfica de f y el eje 0X.
BLOQUE 4
A) Los atletas veteranos de un club de atletismo tienen la siguiente preferencia referente a su
participación en distintos tipos de carreras:
El 70% suele participar en carreras de maratón (42 Km 195 metros)
El 75% suele participar en carreras de media maratón (21 Km 97'5 metros)
El 13% no suele participar en estos tipos de carreras.
Se elige al azar uno de estos atletas. Calcula la probabilidad de que:
a) Suela participar en carreras de maratón o de media maratón.
b) Suela participar en carreras de maratón y de media maratón.
c) Suela participar únicamente en carreras de maratón o únicamente en carreras de media maratón.
B) En una prueba ciclista de contra-reloj, la variable aleatoria: "Tiempo que tarda el corredor en
recorrer la distancia de 22 Km" se distribuye normalmente con una desviación típica de 3 minutos.
Queremos estimar la media de la población. ¿Cuál es el tamaño mínimo que debería tener la
muestra que hemos de tomar si queremos que el nivel de confianza sea del 94% y el error
admisible no supere el valor de 0'8?
SOLUCIONES
BLOQUE 1:
A) a) 2/3 b)3/5 c) 37/90
B) 40 de la Oferta I y 60 de la II.
BLOQUE 2:
A) a)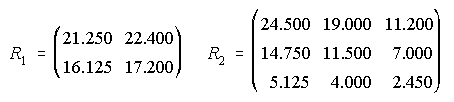
b) 22.400 €, 2.450 € c)Elemento 11 de R1. d) 38.450 €.
B)El número es el 123
BLOQUE 3:
A) a) Crece de 10 a 12 y de 15 a 19 horas
b) A las 12 horas. 1.240 pts. c) A las 15 horas. 700 pts. d) A las 19 horas. 6.140 pts.
B) a) Es continua. c) 4/3 u2.
BLOQUE 4:
A) a) 0'87 b) 0'58 c) 0'29
B) 50
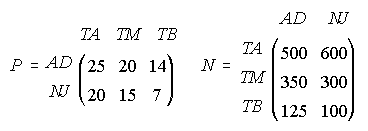 . Se pide: (a) Obtener, si es posible,
las matrices R1=P.N y R2=N.P (b) ¿A cuántos euros asciende la recaudación total correspondiente
a los niños y jubilados? ¿Y la correspondiente a la Temporada Baja? (c)¿Qué elemento de R1 o R2
nos proporciona información sobre la recaudación total correspondiente a los adultos? (d) ¿A
cuántos euros asciende la recaudación total?
. Se pide: (a) Obtener, si es posible,
las matrices R1=P.N y R2=N.P (b) ¿A cuántos euros asciende la recaudación total correspondiente
a los niños y jubilados? ¿Y la correspondiente a la Temporada Baja? (c)¿Qué elemento de R1 o R2
nos proporciona información sobre la recaudación total correspondiente a los adultos? (d) ¿A
cuántos euros asciende la recaudación total?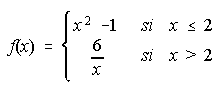 . Se pide:
. Se pide: