UNIVERSIDAD DE CASTILLA-LA MANCHA

Pruebas de aptitud para acceso a la Universidad (Bachillerato L.O.G.S.E.)

Materia: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II

Esta prueba consta de cuatro bloques de dos ejercicios A) y B) cada uno. El/la alumnos/a debe resolver cuatro ejercicios, uno de cada bloque. Cada ejercicio tiene una puntuación máxima de 2,5 puntos. Se puede utilizar cualquier tipo de calculadora.

BLOQUE 1

A) Los consumos de agua mineral, pan y leche de tres familias vienen expresados en la matriz A. La evolución de los precios de los años 1.995 a 1.998 viene reflejada en la matriz B.

i) Halla, si es posible, A.B y B.A e indica qué información proporciona el producto matricial.

ii) ¿Qué información nos da el elemento c₃₄ de la matriz producto?

B) Sumando los años de antigüedad de tres empleados A, B y C se obtienen 50 años. El doble de la suma de las antigüedades de B y C es igual al triple de la antigüedad de A. La diferencia de antigüedad entre B y C es igual al 30% de la antigüedad de A. Determina los años de antigüedad de cada empleado.

BLOQUE 2

A) Dada la función objetivo f(x,y)=2x+3y sujeta a las restricciones:

2x+ y<10 ; x+2y< 8 ; x>0 ; y>0

Se pide: i) Representa la región factible.

ii) Halla los valores de x e y que hacen máxima la función objetivo.

iii) Determina los valores de x e y que minimizan la función objetivo.

B) Se ha realizado un estudio entre 800 estudiantes obteniéndose los siguientes datos: Hay 440 mujeres de las cuales cursan estudios técnicos 300 y el resto estudian humanidades. De los 360 varones 200 cursan estudios técnicos y 160 humanidades. Se selecciona al azar un alumno. Se pide: i) Probabilidad de que estudie humanidades si se sabe que es varón.

ii) Probabilidad de que la persona elegida sea mujer si se sabe que realiza estudios técnicos.

iii) ¿Son independientes los sucesos ser varón y estudiar humanidades?

BLOQUE 3

A) Dada la función siguiente, se pide:

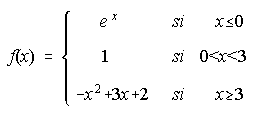
i) Gráfica de f(x). ii) Estudia la continuidad y derivabilidad de f(x).

iii) Calcula la pendiente de la recta tangente a f(x) en el punto de abcisa 4.

B) Se ha estudiado el rendimiento de los empleados de una oficina a medida que transcurre la jornada laboral (Dicho rendimiento corresponde al número de instancias revisadas en una hora). La función que expresa dicho rendimiento es: R(t)=30t-10,5t²+t³, siendo t el número de horas transcurridas desde el inicio de la jornada laboral.

i) Determina cuándo se produce el máximo rendimiento y cuándo el mínimo rendimiento.

ii) Halla la tasa de variación media del rendimiento R(t) entre t=2 y t=4.

BLOQUE 4

A) Un laboratorio ha preparado un elevado número de dosis de una cierta vacuna. Se conoce que el peso de dichas dosis se distribuye normalmente con una desviación típica de 0,10 mg. El peso medio de las dosis ha de ser 0,70 mg. Se requiere la máxima precisión en el peso de las dosis, por ello se elige una muestra de 200 dosis y se comprueba su peso medio que resulta ser 0,66 mg. Realiza un contraste de hipótesis con un nivel de significación de 0,05 para decidir si se deben retirar las dosis producidas, o bien la diferencia de peso medio es debida al azar. Indica que se entiende por hipótesis nula e hipótesis alternativa.

B) Una urna contiene 2 bolas negras y 2 bolas blancas. Se realizan cuatro extracciones con reemplazamiento. Se pide:

i) Obtén el espacio muestral correspondiente a este experimento aleatorio.

ii) Determina qué elementos del espacio muestral constituyen el suceso A:"Sólo sale una bola negra" y cuáles el suceso B:"La segunda bola extraída es negra".

iii) Halla las probabilidades correspondientes a los sucesos A y B y las correspondientes a su unión y su intersección.