UNIVERSIDAD DE CASTILLA-LA MANCHA

Pruebas de acceso a la Universidad (BACHILLERATO L.O.G.S.E.)

MATERIA: MATEMÁTICAS II Esta prueba consta de cuatro bloques de dos preguntas cada uno. El alumno debe contestar solamente a dos de los bloques. Todas las preguntas puntúan igual (de cero a 2,5 puntos).

---------------------------------------------

PRIMER BLOQUE

A) Los puntos A(1,2,0) B(2,5,0) y C(3,3,1) son tres vértices consecutivos del paralelogramo ABCD. Se pide:

(i) Coordenadas del vértice D.

(ii) Coordenadas del centro del paralelogramo.

(iii) Distancia del vértice B a la diagonal AC.

B) Estudia la continuidad y derivabilidad de la función f(x) = x²+2+|2x+1| en el conjunto de los números reales. ___________________________________________________________________________

SEGUNDO BLOQUE

A) Determina los extremos relativos, concavidad y asíntotas de la función

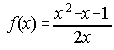
B) Halla la ecuación de un plano que contiene a la recta "r" de ecuaciones 3x-2y-5=0; x+z+1=0 y es perpendicular al plano 2x-3y+z-4=0.

___________________________________________________________________________

TERCER BLOQUE

A) Estudia la compatibilidad del sistema de ecuaciones y resolverlo cuando tenga solución.

B) Calcular .

___________________________________________________________________________

CUARTO BLOQUE

A) Dadas las funciones f(x) y g(x), se pide: (i) Dominio de las funciones f y g.

(ii) Calcula los siguientes límites:

.

B)Estudia, según los valores de "t", el rango de la siguiente matriz:

SOLUCIONES:

PRIMER BLOQUE:

A. i) (2,0,1) . . . ii) (2,5/2,1/2) . . . .iii) 2'41523

B. Continua en y derivable en R-{½}

SEGUNDO BLOQUE:

A. No tiene exteremos relativos.

Cóncava hacia arriba (-inf,0), cóncava hacia abajo (0,inf). A.V.: x=0, A.O.: y=1/2x-1/2

B. x+2y+4z+9=0

TERCER BLOQUE:

A. t=1 SI. t distinto de 1 SCD

B.

CUARTO BLOQUE:

A. i) Domf(x)=R-{2/3}; Domg(x)=R-{1} ii) e , infinito

B. t=-1 rg(A)=2, t-1 rg(A)=3