UNIVERSIDAD DE CASTILLA-LA MANCHA

Pruebas de acceso a la Universidad (BACHILLERATO L.O.G.S.E.)

MATERIA: MATEMÁTICAS II Esta prueba consta de cuatro bloques de dos preguntas cada uno. El alumno debe contestar solamente a dos de los bloques. Todas las preguntas puntúan igual (de cero a 2,5 puntos).

---------------------------------------------

PRIMER BLOQUE

A) Determina a y b para que f(x) sea continua en x=-1 y x=1

Para los valores de a y b obtenidos anteriormente, estudia si f(x) es derivable en x=1.

B) Estudia si las rectas r y s son coplanarias. En caso afirmativo, da la ecuación del plano que las contiene.

___________________________________________________________________________

SEGUNDO BLOQUE

A) Halla la ecuación de la recta tangente a y=x²+2, en el punto de abscisa x=1. Calcula el área del recinto limitado por y=x+2, la tangente anterior y el eje OY.

B) Determina la matriz X, sabiendo que X·A²+B·A=A², siendo:

________________________________________________________________________

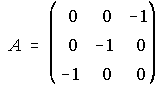
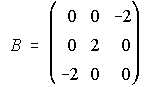
TERCER BLOQUE

A) Estudia el rango de la matriz A, según los valores de t. Razona si para algún valor de t, existe A^-1.

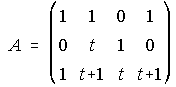
B) Estudia la concavidad y convexidad de la función f(x). Determina si tiene puntos de inflexión.

___________________________________________________________________________

CUARTO BLOQUE

A) Calcula la integral

B) Halla la ecuación de la recta que pasa por P:(3,-4,7) y es perpendicular al plano

2x-3y+z-11=0. Halla el punto simétrico de P respecto del plano .

SOLUCIONES:

PRIMER BLOQUE:

A. a=2, b=0. No derivable

B. Son coplanarias 6x+5y-7z+11=0

SEGUNDO BLOQUE:

A. y=2x+1 1/2 u²

TERCER BLOQUE:

A. Si t no es 0 rg(A)=3. Si t=0 rg(A)=2. No existe la inversa.

B. Cóncava hacia arriba (-inf,-1),(1,inf). Cóncava hacia abajo (-1,1).

Punto de Inflexión: (-1,2) y (1,2)

CUARTO BLOQUE:

A. x+20/3 lnx-4-5/3 lnx-1

B. x=3+2t; y=-4-3t; z=7+t. (-1,2,5)