UNIVERSIDAD DE CASTILLA-LA MANCHA

Pruebas de aptitud para el acceso a la Universidad (BACHILLERATO L.O.G.S.E.)

MATERIA: MATEMÁTICAS II Esta prueba consta de cuatro bloques de dos preguntas cada uno. El alumno debe contestar solamente a dos de los bloques. Todas las preguntas puntúan igual (de cero a 2,5 puntos).

_______________________________________

PRIMER BLOQUE

A) Halla los máximos y mínimos relativos, los puntos de inflexión y los intervalos de crecimiento y de decrecimiento de la función:

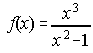
B) Discute y resuelve, según los diferentes valores del parámetro a, el sistema de ecuaciones lineales:

____________________________________________________________________________

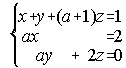
SEGUNDO BLOQUE

A) Dadas las rectas r y s halla los puntos que dan la mínima distancia y determinar la ecuación de la perpendicular común a ambas rectas.

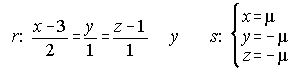
B) Calcula el siguiente límite:

____________________________________________________________________________

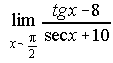
TERCER BLOQUE

A) Determina la matriz X que verifica: AXA-B=0, siendo las matrices:

, .

B) Calcula .

____________________________________________________________________________

CUARTO BLOQUE

A) Halla la distancia del punto P(1,2,3) a la recta r, determinando el punto de la recta que dista menos de P.

B) Halla el área del recinto limitado por las gráficas de las funciones y=x²-2x e y=-x²+4x.

SOLUCIONES:

PRIMER BLOQUE:

A. Crece, decrece. Máximo,

mínimo. Punto de inflexión en (0,0)

B. Si a=0, a=1 ó a=-2 SI. Si a no es 0, ni 1 ni -2 SCD Solución:

SEGUNDO BLOQUE:

A. x=-5/7-2t; y=t; z=20/7+3t (8/7,-13/14,1/14) con r y (5/7,-5/7,5/7) con s.

B. 1

TERCER BLOQUE:

CUARTO BLOQUE:

A. (2,4,4)

B. 9 u²