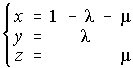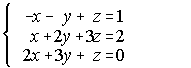
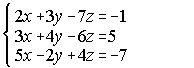
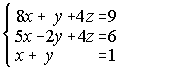
-- SISTEMAS DE ECUACIONES --

1. Resuelve por el método de Gauss los siguientes sistemas:

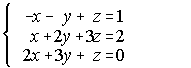
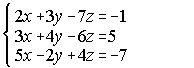
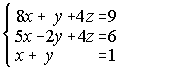
2. Las cifras de un número suman 18. Si a ese número se le resta el que resulta de invertir el orden de sus cifras, se obtiene 594; la cifra de las decenas es media aritmética de las otras dos. Halla dicho número. (El sistema debe resolverse aplicando el método de Gauss).

3. Discute según los valores del parámetro a los siguientes sistemas de ecuaciones:

; . . . . . . ; . . . . .

; . . . . . . ; . .

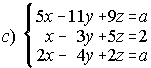
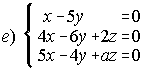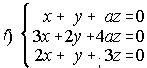
4. Dado el sistema determina m para que tenga:

a) Solución única.. . . . b) Solución múltiple. . . . . c) La solución x=0.

d) La solución x=8. . . e) La solución x=K. . . . . . f) Para que sea incompatible.

5. Dado el sistema siguiente: . . . a) Halla el valor de K que hace el sistema incompatible.

b) Halla el valor de K para el cual el sistema es compatible y además z=-1.

c) Para el valor de K hallado en b), resuelve el sistema.

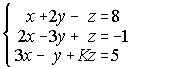
6. Demuestra que el sistema siguiente tiene solución si K no es 8. Resuelve el sistema si K=8.

7. Discute según los valores del parámetro a los siguientes sistemas:

; . . . . . . . .

8. Resuelve los siguientes sistemas por el método de Cramer:

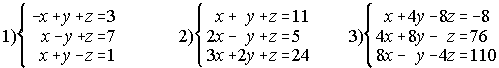
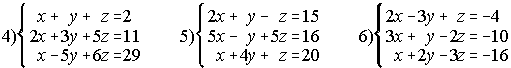
9. Discute los siguientes sistemas según los valores del parámetro a, resolviendo los casos compatibles:

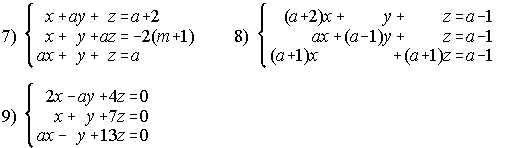
10. Halla m para que los siguientes sistemas tengan soluciones distintas de la trivial y resolverlos:

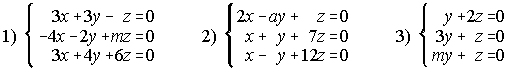
11. Sea el sistema de ecuaciones

a) Resuelvelo determinando x e y en función de a. . . . b) Calcula a para que x + y = 1.

12. Dado el sistema siguiente . Halla m para que: a) No tenga solución.

b) Tenga infinitas soluciones. . . . c) Tenga solución única. . d) Tenga una solución en la que x= 3.

13. Discute los siguientes sistemas según los valores del parámetro m, resolviendo los casos compatibles:

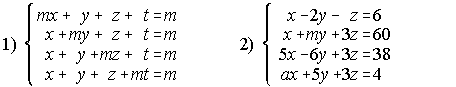
14. Dado el sistema

a) Añade una ecuación lineal de forma que el sistema resultante sea incompatible.

b) Añade una ecuación lineal de forma que el sistema resultante sea compatible e indeterminado. Resuelve el sistema así formado.

15. Halla el menor valor posible de t entre los números naturales tal que el sistema tenga solución.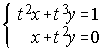 . . . . Resuelvelo.

16. En un sistema de ecuaciones la matriz de los coeficientes es la siguiente . Los términos independientes son por este orden 1, 2, a. Determina el valor de a para que el sistema sea compatible. Eligiendo un valor adecuado de a, comprueba que se puede suprimir una ecuación, resultando un sistema equivalente al dado. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (Septiembre 88)

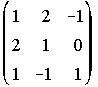
17. Discute el sistema: según los valores del parámetro t, y resuelvelo cuando sea compatible.

. . . . . . . .(Septiembre 89)

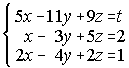
18. Discute el sistema según los valores del parámetro t. Resuelvelo cuando sea posible.

. . . . . . . .(Septiembre 90)

19. Discute el siguiente sistema de ecuaciones según los valores del parámetro t. Resuelve el sistema anterior, si es posible, para t=0. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (Junio 93)

20. Discute el siguiente sistema de ecuaciones, según los valores del parámetro t, y Resuelvelo cuando sea compatible indeterminado: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (Septiembre 93)

21. Estudia si existe algún valor de m, para el cual el sistema es compatible. Si es así, Resuelve el sistema para ese valor de m: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (Junio 94)

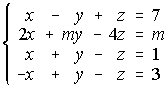
22. Discute, para los diferentes valores de m, el siguiente sistema de ecuaciones lineales: Resuelve el sistema (si es posible) para m=-1. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (Septiembre 94)

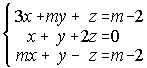
23. a) Estudia la compatibilidad, en función del parámetro m, del sistema: b) Resuelvelo para m=2.

(Septiembre 2.000)

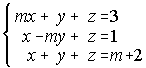
24. Clasifica según los valores del parámetro "a" y resuelve cuando sea posible:

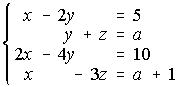. . . . . . . . . . . . . (Propuesto 2.001)

25. Discute y resuelve, en los casos sea posible, el siguiente sistema: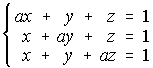

(Propuesto 2.001)

SOLUCIONES

1. a) x=1; y=-1; z=1 . . . b) x=-1; y=5; z=2 . . . . c) x=t; y=1-t ; z=(8-7t)/4

2. 963

3. a) SCD . . . b) a no es 9/2 SCD, a=9/2 SI . . . c) a=-2 SCI, a no es -2 SI

d) a=4 SCI, a no es 4 SI . . . . e) a=3 SCI, a no es 3 SCD . . . f) a=1 SCI, a1 SCD

4. a) m no es -2 . . . . b) Nunca . . . . c) m=-1 . . . d) Nunca . . . . e) (2K-8)/(8-K) . . . . f) m=-2

5. a) k=0 . . . . b) k=2 . . . . c) x=3, y=2, z=-1

6. x=(4-5t)/3; y=(-2+t)/3; z=t

7. a) a no es 1 ni -2 SCD ; a=1 SCI ; a=-2 SI . . . . . b) a no es1 ni -3 SCD ; a=1 SCI ; a=-3 SI

8. 1) x=4, y=2, z=5 . . . . . 2) x=4, y=5, z=2 . . . . . 3) x=16, y=2, z=4 . . . . . 4) x=1, y=-2, z=3

5) x=5, y=4, z=-1 . . . . . . 6) x=1, y=5, z=9

9. 1) Siempre es compatible: x=2a/3-1, y=2-a/3

2) Si a no es ±2 SCD: x=6/(a+2), y=3/(a+2) ; Si a=2 SCI: x=3-2t, y=t; Si a=-2 SI.

3) Si a=0 SI; Si a=-1 SI; Si a no es 0 ni -1 SCD: x=2(a+2)/(a+1), y=-(a+3)/(3a(a+1))

4) Si a=8/3 SI; Si a=1 SI; Si a no es 8/3 ni 1 SCD:

, ,

5) Si a no es 1 ni -2 SCD: x=y=z=1/(a+2) . . . Si a=1 SCI: x=1-y-z . . . Si a=-2 SI.

6) Si a no es 1 ni -2 SCD: , , Si a=1 SCI , x=1-y-z . . Si a=-2 SI.

7) Si a no es 1 ni -2 SCD: , ,

Si a=1 SI; Si a=-2 SCI: x=(3t+4)/3, y=(3t+2)/3, z=t

8) Si a no es 0 ni 1 ni -1 SCD: , ,; Si a=-1 SI . . . Si a=0 SCI: x=-1-t, y=1+t, z=t . . . Si a=1 SCI: x=-t, y=2t, z=t.

9) Si a no es 3 ni -12/7 SCD: solución trivial . . . Si a=3 SCI, x=-5t, y=-2t, z=t;

Si a=-12/7 SCI: x=28t, y=-35t, z=t.

10. 1) m=46/3; x=22t/3, y=-7t, z=t . . . 2) a=-36/5; x=-19t/2, y=5t/2, z=t. . 3) Ningún valor de m.

11. x=cosa+sena, y=sena-cosa; ó

12. 1)m=-1; . . . 2)m=1; . . . 3)si m no es 1 ni -1; . . . 4)m=-2/3.

13. 1) Si m no es 1 ni -3 SCD: x=m/(m+3)=y=z=t; . . . . Si m=-3 SI; . . . . Si m=1 SCI.

2) Si m no es -7 ni -25/7 SI; . . Si m=-7 SCD: x=-26/7,y=-50/7 z=32/7; . .Si m=-25/7 SCD: x=-14, y=-14,z=8.

14. 2) x=(-t+7)/5, y=(t-2)/5, z=t.

15. Si t no es 0 ni 1 SCD: x=1/(t(t-1)), y=-1/(t³(t-1)) ; . . . Si t=0 SI; . . . Si t=1 SI;

t=2 y solución es x=1/2 , y=-1/8.

16. a=1 SC, se puede suprimir la 3ª ecuación.

17. Si t no es 4 SI; Si t=4 SCI: x=-5/2+7t, y=-3/2+4t, z=t.

18. Si t no 0 ni 1 SCD: solución trivial; Si t=0 SCI: x=-3t, y=2t, z=0; Si t=1 SCI: x=-2t, y=t, z=t.

19. Si t no es 0 ni 1 SCD; Si t=1 SI; Si t=0 SCI: x=1-t, y=t, z=-1.

20. Si t no es 0 ni 1 SCD: x=t/(t-1), y=-1/(t-1), z=t/(t-1) ; Si t=1 SI; Si t=0 SCI: x=1-t, y=t, z=0.

21. SI para todo valor de m.

22. Si m no es -2 ni 2 SCD; Si m=2 SCI; Si m=-2 SI; Si m=-1 SCD: x=-3, y=-3, z=3.

23. a) Si m=±1 SCI; Si m no es ±1 SCD; . . . . b) x=-1; y=1; z=4.

24. SCD para cualquier valor de a. . . . . . Solución: x=(17+8a)/5 ; y=(4a-4)/5 ; z=(4+a)/5.

25. Si a no es 1 ni -2, SCD. . . . . . . . . Si a=1, SCI. . . . . . . . . . Si a=-2, SI

Caso SCD: x=y=z=1/(a+2) . . . . . . . . Caso SCI: