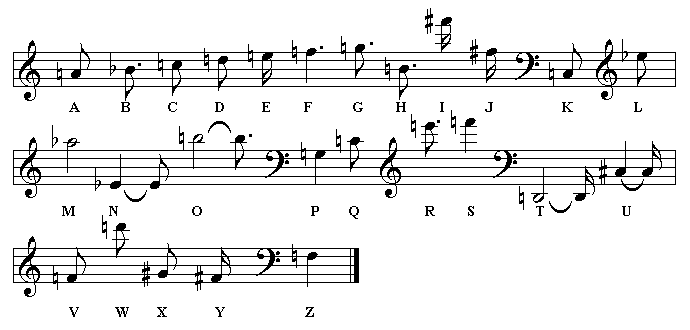
CONSTANTS
Digits of the constant e was used for this piece, which has four parts.
e = 2.71828182845904523536028747135266249775724709369995957...
1) Chords of three tones of the E whole tone scale. Within an octave, there are ten ways to construct such a chord. The current digit determines the tonic and the next digit determines the chord. Equal consecutive tones were tied. The note values are 1. The first 93 digits of e were used.
| Digit | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Chord | 1- 2- 3 | 1- 2- 4 | 1- 3- 5 | 1- 2- 6 | 1- 3- 4 | 1- 3- 5 | 1- 3- 6 | 1- 4- 5 | 1- 4- 6 | 1- 5- 6 |
| Pitch | 1st of next chord | E0 | F# | G# | A# | C | D | E1 | 2nd of next chord | 3rd of next chord |
2) Additional bass tones for the above chords. 5 scale steps below the tonics. Equal consecutive tones were tied.
3) A walking bass line. 0 is a pause, 1 - 7 is the E whole tone scale including the octave, 8 and 9 sustains the previously determined tone. Alternatingly, at every occurrence of the digit 7, the pitch is determined as mentioned or by descending a scale step if the digit is odd and ascending a scale step if the digit is even. Equal consecutive tones were tied. The first 372 digits of e were used.
4) A treble part is initiated at the digit 0 and terminated at the next digit 0 and then initiated again at the next digit 0 and so on... The pitches were determined in the same way as the third part. The note values are 1/2. The first 166 digits of e were used.
Playing time: 6' 15".
This piece (a bit more constructed than usual, perhaps) has four parts using the digits of p.
p = 3.14159265358979323846264338327950288419716939937510582097494...
1) The first, third, fifth etc.. digits of p, digits 1 - 8 is the A harmonic minor scale, 0 is a pause and 9 the same as the previous tone (or pause). Equal consecutive tones were tied. This part begins - after two measures in common time - with sixteenths over eight measures and then eighths over eight measures. The rest is all sixteenths, but to get a wider range, the part was transposed by fifth intervals in some measures in the following way: 1 (or, same as previous measure), +5, -5, +5, +5, -5, -5, -5, +5, 1, 1, 1 and then playing in unison with the other parts to the end.
2) Same as above but using the second, fourth, sixth etc.. digits of p.
3) The digits of p, from the beginning, were mapped to tones like above. Starts with two measures of sixteenths, then eight measures of eighths, then pauses for eight measures and then all sixteenths to the end.
4) LIke the part above but one octave lower, or oscillatingly a third, fifth or seventh below. You'll hear when the mapping procedure changes and I'm too tired.
Playing time: 1' 48".
For the piece below, I used Olivier Messiaen's special musical alphabet which he called "Le langage communicable" (a communicable language). He extended the German names of the notes; A B C D E F G H, by alloting each letter of the alphabet from A to Z its own pitch, octave and note value as shown in the picture.
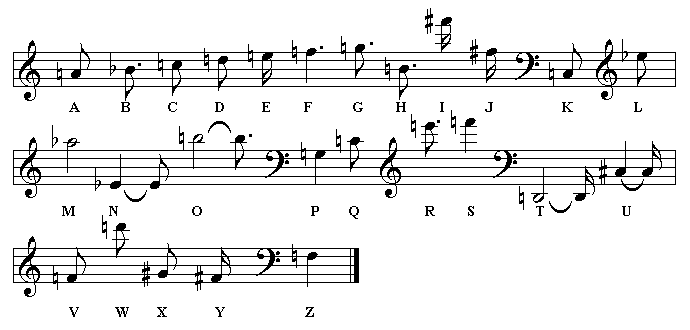
I went through the first 255 decimal digits of p taking two digits at a time. If the value exceeded 26 I took the digits separately and projected the numbers 1 - 26 to the letters A - Z.
p = 3.14159265358979323846264338327950288419716939937510582097494...
Playing time: 3' 14".
1) The walking bass line in the piece are the first 215 decimal digits of the very suitable Copeland-Erdos constant - the prime numbers concatenated:
0.235711131719232931374143475359616771737983899710110310710911...
The digits 1 to 8 is the E harmonic minor
scale, 0 is a quarter pause, 9 means change octave and the 9 itself takes
on the same pitch as the previously dtermined tone but in the new octave
(the piece oscillates up and down over two octaves).
2) The melody is the first 845 decimal digits of the Froda constant,
2e.
2e = 6.580885991017920970851542403886486491573077438348074005121512...
The notes were determined in the same way as in the bass line but are sixteenth notes.
Playing time: 2' 02".
W(1) = 0.567143290409783872999968662210355549753815787186512508135131...
There are two parts in the piece of music:
1) Bassline. Four bars of sixteenth notes in 4/4 time is first determined by mapping two digits at a time between a C octave. Then these four bars will be repeated three times while the treble part is being creative with the following digits. After the treble part is done with this, another four bars is determined and the same thing happens again until the end.
2) Treble part. This part almost copies the bassline the four bars when it's being determined (three times throughout the piece), but two octaves above and switches D's and Eb's with G's and Ab's respectively. Then ad libbing over twelve bars using the scale C D Eb G Ab where the digit 9 switches the octave (the part oscillates over three octaves), 0 is a pause and 7 descends a scale step and 8 ascends a scale step and the digits 1 - 6 make up the ordered scale (including the C an octave higher). Similar for the second ad lib section, but the digits 1 - 7 is the scale C E F G Ab Bb (used in Swedish folk music, with Eb instead of E in the descending version sometimes). Equal consecutive tones are tied in the creative sections.
Playing time: 1' 15".
PS. I tried with a third ad lib section using a combination of the two scales; C D Eb E F G Ab Bb, which sounds nice, but there were a lot of 9's in the end that made it too jumpy-sounding.
The Omega constant W(1) and its inverse 1 / W(1) was used for this piece.
W(1) = 0.567143290409783872999968662210355549753815787186512508135131...
1 / W(1) = 1.7632228343518967102252017769517070804360179866674736345704569...
I guess the piece as a whole is atonal, but a more descriptive term for the tonality might be dynamic pentatonic because each section of the composition uses its own (but not necessarily unique) pentatonic scale determined by the digits by taking two of them at a time from 1 / W(1) (mod 12) and mapping the value to the ordered twelve tone scale E F F# G G# A A# B C C# D D#. The sum of the digits needed to determine a scale multiplied by 3 is the number of digits of W(1) and 1 / W(1) for the section of the piece that will use the scale. The next pentatonic scale will be determined by the first digits of the next section of digits of 1 / W(1). These are the pentatonic scales used in the piece in order of occurrence:
F F# A B C (this scale and the next were determined
by another algorithm, see the note at the bottom)
E G G# A C#
F G# D C D#
F# G# A# C# D
E F G C# D#
F# A C# D D#
F A C C# D
F F# G B D
E G# A A# B
F# G G# A# C
The middle tone of each scale was mapped from 5. So for the first scale with the middle tone A, we have 1 2 3 4 5 6 7 8 9 which maps to B-1 C-1 F0 F#0 A0 B0 C0 F1 F#1.
0 is a pause. Consecutive equal tones are tied. If the first digit of each section of digits of W(1) or 1 / (W) is odd, then the tones are played staccato, otherwise legato. If both those digits are even or odd, then the middle tones are taken one octave down.
There are two parts:
1) A bass part using the first 908 digits of 1 / W(1).
2) A treble bass part (one octave above the first part) using the first 908 digits of W(1).
Playing time: 2' 50".
Note: Regarding the scales; the first two were determined by mapping the first digit of the two first sections of digits of 1 / W(1) to the ordered twelve tone scale given above, and then letting the next digit represent the number of scale steps to the next pitch (with the scale cyclic like a clock). This algorithm is more elegant but I somehow forgot about it and started to determine the scales from the first draft of an algorithm I had where the scales were determined as described above.
This is a canon at the octave in A minor. Two beats in 4/4 time was determined at each step. The first 798 digits of the Omega constant, W(1), was used.
W(1) = 0.567143290409783872999968662210355549753815787186512508135131...
Digits 1 - 8 is the A natural minor scale, 0 is a pause and 9 is the same as the previously determined tone. Consecutive tones of equal pitch are tied. The range for each part is two octaves. If the first tone of a two beat pattern was determined by an odd digit, then pitches are of the lower octave, otherwise the upper octave.
After initiating the piece over two bars the recursion steps in. If the note values of the two beat patterns two measures back were eighths, then the new notes will be sixteenths and vice versa.
Playing time: 2' 56".
This piece consists of the first 508 decimal digits of the Ramanujan number, epÖ163.
epÖ163= 262537412640768743.9999999999992500725971981856888793538563373...
The duration of each note was determined by the next digit. The notes given by the digits 5 - 9 are one octave above the notes given by the digits 0 - 4. For every digit 9; if the next digit is not 9, then the next digit will be doubled by the digit after 9.
| Value | ||||||
| Digit | 0 | 1 | 2 | 3 | 4 | 1/4 |
| 5 | 6 | 7 | 8 | 9 | 1/8 | |
| Pitch | C | Db | F | G | Ab | |
Playing time: 3' 15".