from CHAPTER XI: "GIANT BIRDS"

The largest modern birds cannot fly. They are the ostrich (up to 120 kg), cassowaries (60 kg), the emu (50 kg) and the Emperor penguin (40 kg). With the exception of the penguin, these are members of the group called the ratites, which also includes the rheas and kiwis.

Ostriches and other ratites are like enormously overgrown chicks. They have tiny wings, useless for flight¹, and well-developed legs. They have puffy plumage instead of the blade-like feathers of other adult birds. They also have some chick-like features in their skeletons. They are believed to have evolved by processes of development getting out of step with each other: they grow large and sexually mature while keeping a lot of juvenile features².

The biggest extinct birds are also ratites. They are the moas, which lived in New Zealand, and the elephant birds, in Madagascar. The biggest moa is Dinornis maximus, 3.5 meters tall (twice the height of an average man). The biggest elephant birds looked very similar and were about 3 meters tall. There were also some giant birds that were not ratites. Diatryma, a wicked-looking predator that lived in North America, was about 2 meters tall. It lived quite early in the Cenozoic era but the moas and elephant birds are more recent. Indeed, the moas survived in New Zealand until after the Maoris arrived.

I have made scale models of moas and used them to estimate the masses of the living birds, in much the same way as I estimated the masses of dinosaurs (chapter 2). I modeled the main features of the skeleton in wire and then added clay to represent the flesh, making models that represented the birds as if they had been plucked. I measured the volumes of the models and used them to calculate the masses of the plucked birds, assuming that their densities were the same as the density of a plucked goose carcase (which I measured). Finally, I added an allowance for the feathers, which I assumed to be the same fraction of body mass as in turkeys and kiwis. The result for a big Dinornis was 240 kilograms, about the same as a large tiger. The biggest elephant birds were stouter, although they were a little shorter, and may have been nearly twice as heavy³.

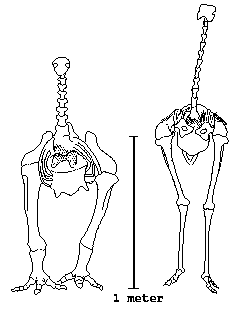FIGURE 11.3
Skeletons of (left) Pachyornis and an ostrich, to the same scale. From Alexander 1983a.

Though Dinornis was the biggest moa, the one that fascinates me is Pachyornis elephantopus shown in figure 11.3. Its splendid name means "fat⁴ bird with elephant's feet," and seems very suitable. Its leg bones were amazingly thick. Compare it with the ostrich, drawn beside it to the same scale. I estimate this moa's mass as 130 kilograms (from measurements on a model) and the ostrich, whose skeleton is illustrated, as only 68 kilograms, but even so the moa bones look disproportionately thick.

Appearance can be deceptive, so I measured the moa's bones and calculated strength indicators in the same way as for dinosaurs (chapter 4⁵). The results are shown in table 11.1. The value for the tibiotarsus (shin bone) is about the same as for an ostrich, and those for the other two bones are twice as high as for the ostrich. To be consistent with my line of argument in chapter 4, I should conclude that Pachyornis was at least as athletic as ostriches, but I find that hard to believe. Ostriches are exceedingly fast runners, probably faster than the African antelopes. Should I conclude that moas were also exceedingly fast? I cannot believe that they were with those clumsy-looking legs.

TABLE 11.1. Strength indicators (Z/W _X , see p. 53⁶) for leg
bones of an ostrich and the moa Pachyornis elephantopus.

Strength indicator (square meters per giganewton) for:

	Femur	Tibiotarsus	Tarsometatarsus
ostrich	45	18	17
moa	94	17	39

The key to the problem may be that moas seem to have had no need to run. They fed on plants, as remains of their stomach contents show, so they had no need to run to capture food. There seem to have been no predators in New Zealand, until the Maoris arrived, so there was nothing to run away from. (That is to say, there was nothing to run away from while they were evolving. They seem to have been easy prey to the Maoris, who hunted them to extinction.) It was not the same for the dinosaurs: the flesh-eating dinosaurs had to run to catch prey and the plant-eating ones had to run to escape. This difference between moas and dinosaurs may justify a different interpretation of their strength indicators.

My idea involves safety factors. Suppose an engineer is designing a small bridge to carry a maximum load of ten tonnes. He would be an optimist if he calculated the thickness of steel that could just support ten tonnes without breaking, and ordered steel that thick. Any reputable engineer would allow a safety factor: he might design the bridge to be able to carry twenty tonnes although he expected the maximum load to be only ten. The reason for this is that neither load nor strength can be predicted precisely. An unexpectedly large load may arrive, or the steel may be substandard, and in either case a bridge that was expected to be strong enough may fail. The bigger the safety factor the less likely this is to happen.

A stronger bridge is less likely to fail but costs more to build. Beyond a certain point, the slight advantage of extra safety obtained by making it stronger still is not worth the extra cost. The ideal strength depends on the cost of the materials. If we had to make bridges of platinum we would make them weaker and live more dangerously. If cheap second-hand steel were available we might make the bridge extra strong.

The evolution of skeletons has also involved balancing safety against cost. In this case the cost is partly the cost in energy and materials of growing a stronger bone, but is largely the penalty of having to carry extra bone around. Thick leg bones may be less likely to break in a fall, but they make it harder to run fast, just as people find it hard to spring in heavy boots. Measurements and calculations on ostriches and several kinds of mammal have shown that their leg bones are about three times as strong as is necessary to withstand the forces involved in strenuous activities such as running and jumping. These bones are built to safety factors of about three, and so can stand many of the larger forces that occur accidentally, for example in falls and collisions.

Moas may have had larger safety factors. However strong their bones, there would always be some danger of an accident bad enough to break them. If they had no need to run, they might not be inconvenienced much by heavy bones. The cost of extra strength might be less for them than for ostriches, which have to run to escape from lions. If strength were cheap, ideal safety factors would be high, which may explain the remarkably thick leg bones of Pachyornis and (to a lesser extent) other moas [and elephant birds] .

Several sets of moa footprints have been found and I have calculated speeds for them, in the same way as for dinosaurs (chapter 3⁷). All of them seem to have been moving between 0.8 and 2.0 meters per second, which have been walking speeds. This does not prove that they never ran, but at least it does not contradict the suggestion that they were not very athletic.

My belief, that moa leg bones had high safety factors, has been challenged. Paleontologist in Tübingen have suggested that moas may have lived in thick undergrowth and may have needed very strong legs to force their way through. I find that hard to believe. An animal that behaved like a bulldozer would use a lot more energy than one that slipped through small gaps, or avoided the densest patches of vegetation, and might be a poor competitor. Nevertheless, the possibility should be considered.

The legs of elephant birds are little less remarkable than the legs of moas, but it is their eggs that I want to write about, the biggest of all known eggs. Quite a lot of elephant-bird egg shells have been found in Madagascar, some with the bones of embryos still inside them. The eggs of the biggest species are 30 centimeters long⁸ with a volume of 9 liters (2.4 U.S. gallons). Ostrich eggs are only about half as long, with a volume of 1.3 liters, and the eggs of all modern reptiles are much smaller. Even known dinosaur eggs are smaller than elephant bird eggs: the biggest I know of are only 25 centimeters long.

Let us think what problems there might be, for very large eggs. First, there is the problem of ventilation. Bird embryos are not hermetically sealed in their eggs, like cans of soup. The eggshell is porous, allowing gases to diffuse in and out. This enables the embryo to get the oxygen it needs for respiration, and to get rid of waste carbon dioxide.

Think of two eggs, one twice the length of the other. It has eight times the volume of the smaller egg, and the embryo in it, just before hatching (when it uses oxygen fastest), is eight times as heavy. The big embryo uses oxygen faster than the small one, but not eight times as fast, because rates of oxygen consumption are not strictly proportional to body mass either for adult animals (figure 7.1) or for embryos. The large embryo will probably use oxygen only four or five times as fast as the small one.

The more pores there are, or the wider the pores, the faster oxygen can diffuse in. However, the thicker the shell, the further the oxygen has to diffuse and the lower the rate of diffusion. The maximum rate of diffusion that a shell allows is proportional to

number of pores × area of each pore
thickness of shell

If two eggs were precise scale models of each other they would have equal numbers of pores and the larger one would have pores of twice the diameter, therefore four times the cross-sectional area, but its shell would be twice as thick. If would allow oxygen to diffuse just twice as fast but the embryo in it would need oxygen, as we have seen, four or five times as fast. This tells us that big eggs need more porous shells than small ones. An excessively big egg would need a shell so riddled with pores as to be seriously weakened. If this shell were made thicker, to strengthen it, it would have to be more porous still. The need to be sufficiently porous must set an upper limit to the sizes of eggs.

Even elephant bird eggs are probably a long way from that limit. Chicken eggs have very sparse pores, piercing only 0.02 percent of the area of the shell. Ostrich eggs have to be much more porous, with 0.2 percent of their area accounted for by pores. Elephant bird eggs must have been more porous still, but even if the pores were 2 percent of their area the shells would not be seriously weakened. I know no measurements of their pores so I cannot state the exact percentage.

Elephant bird eggs may be near an upper size limit, for a different reason. Eggs have to be strong enough to withstand the forces that act on them, when the parent birds get on and off the nest, but they must be weak enough for the hatching chick to break its way out. Think again of two eggs, one twice as long as the other and eight times as heavy. It probably needs to be more than eight times as strong. This is because big birds are heavier, relative to the masses of their eggs than small ones: very small birds are about five times as heavy as their eggs but ostriches are fifty times as heavy as their eggs. The big egg seems to need to be more than eight times as strong, but if its shell is just twice as thick, it will only be four times as strong. (It is a general rule for objects of the same shape, made of the same material, that strength is proportional to (length)²). This means that bigger eggs need relatively thicker shells. An egg that is twice as long as another is generally found to have a shell three times as thick⁸. The eggshell is 4 percent of the mass of a hummingbird egg but 17 percent of the mass of an ostrich egg.

Hatching chicks break their eggs open by hammering at the shell. When you break something by hammering or by any other kind of impact, what decides whether it breaks or not is the energy of the blow. A heavy hammer brought down fast has more kinetic energy than a light hammer moving slowly, and is more likely to break things. Theory tells us that the energy needed to break egg shells should be about proportional to the masses of the chicks and so to the masses of the egg contents (since the hatching chick fills the shell). If bigger eggs have relatively thicker shells, it will be harder for their chicks to break out of them. Too big an egg would be an unbreakable prison.

One final thought about elephant birds: they must have been blessed with patience. Small eggs hatch soon but big eggs take longer. Very small bird eggs hatch in about 15 days, and ostrich and emu eggs take about 50 days. If the trend continues, elephant bird eggs would have taken about 90 days to hatch.

Principal Sources

• Alexander, R.McN. 1981. Factors of safety in the structure of animals. Science Progress 67:109-130.
• Alexander, R.McN. 1983a. Allometry of the leg bones of moas (Dinornithes) and other birds. Journal of Zoology 200:215-231.
• Alexander, R.McN. 1983b. On the massive legs of a moa (Pachyornis elephantopus, Dinornithes). Journal of Zoology 201:363-376
• Anderson, J.F., H. Rahn, and H.D. Prange. 1979. Scaling of supportive tissue mass. Quarterly Review of Biology 54:139-148.
• Rahn, H., A. Ar, and C.V. Paganelli. 1979. How bird eggs breathe. Scientific American 240(2):38-47.
• Tullet, S.G. 1984. The porosity of avian eggshells. Comparative Biochemistry and Physiology 78A:5-13.
• Reif, W.E. and H. Sylin-Roberts. 1987. On the robustness of moa leg bones. Neues Jahrbuch für Geologie und Paläontologie, Monatshefte 1987:155-160.

---

Notes on this text

1. Ostrich wings are too small to bear the bird aloft, but is "tiny" fair? It's all relative. The wings are rather large, all things considered, and are deployed prominently for courtship display.



2. The author clearly weighs in as "pro" for the Neoteny theory about ratite development. For what it's worth, I agree.



3. I'll include the methodology here as soon as I retrieve this reference.



4. Dean Amadon's 1947 estimate was ca. 1,000 lbs (454 kg) which is pretty close.



5. "Pachy-" is usually translated as "thick" (e.g. pachyderm: "thick skin"). Still, "thick bird" seems rather a strange turn of phrase, so Alexander's translation is considered.



6. As with #3, I'll include the methodology here as soon as I retrieve this reference.



7. Some specimen Vorompatra eggs are at least 34 cm. long.



8. This is often called Galileo's square-cube law: while mass increases to the cube as it expands in three dimensions, the cross-section of the supporting structure retaining the original proportions only increases to the square as it expands in two dimensions. An egg twice as long has ("twice cubed" or 2³ =) eight times the mass of the original, and therefore needs roughly eight times as much support. A shell three times as thick provides ("thrice squared" or 3² =) nine times as much support, which would suffice. By the way, this law is just one reason we need never fear giant mutant ants: the exoskeleton wouldn't support their weight.