1. Een voorwerp
schuift wrijvingsloos in een goot waarvan de vorm op de figuur is aangegeven.
Het stuk CD is een halve cirkel met straal r.
Van welke minimale hoogte h moet men het
voorwerp vanuit rust loslaten opdat het de halve cirkel tot in D zou blijven
volgen?
h = 2 * r
h = 2,5 * r
h = 3 * r
h = 4 * r
2. De
onderstaande grafiek stelt de elastische vervorming voor van een stuk kunststof
onder invloed vaneen kracht F. Hierbij stelt x de uitrekking van
dit stuk kunststof voor.
De verhouding van de arbeid geleverd bij de uitrekking van
P tot Q tot de geleverde arbeid bij uitrekking van 0 tot P is dan:
1
2
3
4
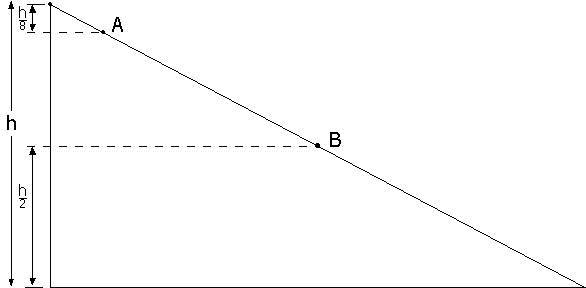
3. Een voorwerp
schuift langs een hellend vlak naar beneden. Het vertrekt vanuit stilstand op
een hoogte h, bereikt het punt A met een snelheid vA en
het punt B met een snelheid vB. Men stelt vast dat de
verhouding vB/vA van deze snelheden gelijk
is aan 1,75. Dit wijst er op dat er niet te verwaarlozen luchtwrijvingskrachten
aanwezig zijn. Als echter de luchtwrijvingskrachten verwaarloosbaar zijn, zal de
verhouding vB/vA gelijk zijn aan:
1,00
1,50
1,75
2,00
4. Een skiër met
massa M neemt deel aan een springwedstrijd. Hij vertrekt uit stilstand
vanop een hoogte h. Hij haalt denodige snelheid op een springschans
waarvan de vorm aangegeven wordt op de figuur. De schans bestaat uit een eerste
stuk dat naar het einde toe mooi overgaat in een cirkelboog met straal R. Je
mag de wrijving verwaarlozen.
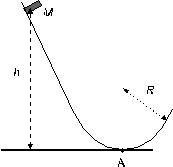
Hoe hoog boven punt A moet hij vertrekken opdat in A de
kracht die de piste op de skiër uitoefent vijf maal zijn gewicht zou bedragen?
R
2 R
2,5 R
5 R
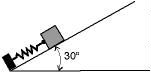
5. Een blok met een
massa van 2 kg kan wrijvingsloos langs een helling verschuiven. De helling maakt
en hoek van 30° met het horizontale vlak. Het blok wordt geplaatst tegen een
veer met een veerconstante k = 2000 N/m. Het blok wordt vervolgens tegen
de veer gedrukt tot deze veer over een afstand van 0,2 m is ingedrukt. Vanuit
deze positie wordt het blok losgelaten.
De
verplaatsing van het blok langs de helling tot het zijn maximale hoogte bereikt
is gelijk aan:
0,2 m
1,0 m
2,0 m
4,0 m
6. Een
kogel vliegt met een snelheid van 100 m/s tegen een harde wand. Al de kinetische
energie van de kogel wordt omgezet in warmte.
De soortelijke warmtecapaciteit van het metaal
van de kogel bedraagt 100 
.
Dan is de temperatuurstijging van de kogel
gelijk aan:
50 °C
100 °C
500 °C
Niet te berekenen omdat de massa van de kogel onbekend is
7. Een
blok van 20 kg beweegt rechtlijnig op een horizontaal parcours langs de x -as.
Op het blok werkt één kracht in. De grafiek
geeft aan hoe de krachtcomponent varieert als functie van x.
In de positie x = 0 is de snelheid van het
blok gelijk aan 4,0 m/s .
Het blok bereikt dan zijn maximale kinetische
energie in de positie gegeven door:
x = 0 m
x = 1 m
x = 2 m
x = 5 m
8. Aan een veer hangt
een blok. Dit blok trekt met een kracht van 100 N aan de veer. De aanwijsnaald
aan de onderzijde van de veer geeft de stand weer op een schaal geijkt in
millimeter. De naald wijst 40 mm aan (zie figuur).
Vervolgens vervangt men de kracht van 100 N
door een kracht van 220 N. De naald wijst dan 70 mm aan. In onbelaste toestand
zal de naald de volgende aanduiding geven op de schaal:
0 mm
10 mm
15 mm
25 mm
9. Een blok van 100 kg beweegt rechtlijnig over een horizontaal parcours.
De netto-krachtcomponent Fx die dat
veroorzaakt is als functie van de positie x voorgesteld in de grafiek.
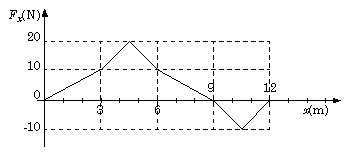
De arbeid door de kracht F op het blok geleverd tussen x = 0 m en x = 12 m is dan gelijk aan:
60 J
75 J
90 J
105 J
10. In volgende
grafiek kan je aflezen hoe de soortelijke warmtecapaciteit c
van een hypothetische stof afhangt van de temperatuur T .
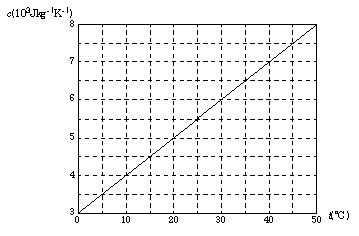
Hoeveel warmte komt er vrij wanneer 1 kg van
dit materiaal afkoelt van 50 °C tot 20 °C?
145 kJ
195 kJ
245 kJ
295 kJ
11. Twee stalen
knikkers 1 en 2 worden gelijktijdig losgelaten uit een punt O op twee vlakken
met verschillende helling (zie figuur). We bekijken de knikkers aan de voet van
de hellingen.
Verwaarloos alle wrijving, dan geldt:
beide knikkers komen met even grote snelheid en op hetzelfde tijdstip aan
de versnelling van 1 is groter dan van 2, maar 1 komt met een grotere snelheid eerst aan
de massa's van 1 en 2 moeten gekend zijn om hun versnelling te kunnen berekenen en uitspraken te kunnen
doen over hun snelheid.
knikker 1 komt eerder aan. De versnelling van 1 is groter dan deze van 2 maar zijn snelheid is even groot als
deze van knikker 2.
12.