1. Iemand duwt
horizontaal tegen een kast. De massa van de kast is 36 kg. De persoon duwt met
een kracht van 40 N. De kast komt niet in beweging.
De wrijvingskracht is op dat ogenblik :
4 N
36 N
40 N
360 N
2. Drie
identieke krachtmeters (dynamometers) en een blokje met massa m zijn verticaal
opgesteld en met elkaar verbonden. De drie krachtmeters zijn correct geijkt voor
gebruik zoals op de figuur aangegeven. De krachtmeters geven respectievelijk 14
N, 12 N en 4 N aan.
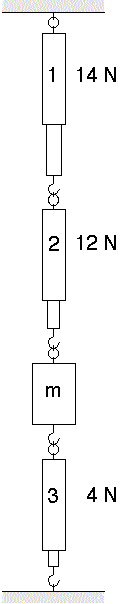
Dan is de massa van het blokje:
1,2 kg
0,8 kg
0,6 kg
0,4 kg
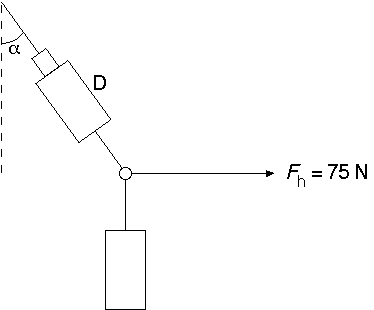
3. Een voorwerp met
een massa van 10 kg hangt aan een dynamometer D. Met een horizontale kracht van
75 N trekt men dit systeem naar rechts. Bij evenwicht vormt de as van de
dynamometer een hoek a met de verticale richting en
wijst de dynamometer een waarde S aan. Dan is:
tg
a = 0,75 en S = 125 N
tg
a = 0,75 en S = 175 N
tg
a = 1,33 en S = 125 N
tg
a = 1,33 en S = 100 N
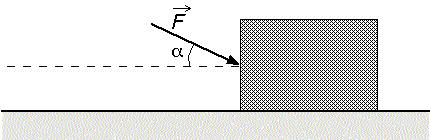
4. Een voorwerp met
massa m schuift onder invloed van een kracht F over een ruwe tafel met
wrijvingscoŽfficiŽnt m . De versnelling van het
voorwerp kan geschreven worden als:
F/m
F . cos
a /m
(F . cos
a - m . m .g) /m
(F . cos
a - m ( m .g + F . sin
a ))/m
5. De onderstaande
figuur toont een stel voorwerpen die aan elkaar verbonden zijn met massaloze
touwen die wrijvingsloos bewegen over katrollen. Het voorwerp met massa 2 M
schuift over een horizontale tafel. M is gelijk aan 2 kg. Alle voorwerpen hebben
een versnelling 1,5 m/s≤.

De grootte van de wrijvingskracht op het blok dat
over de tafel glijdt is gelijk aan:
niet te bepalen als de wrijvingscoŽfficiŽnt niet gegeven is
5,0 N
7,5 N
11 N
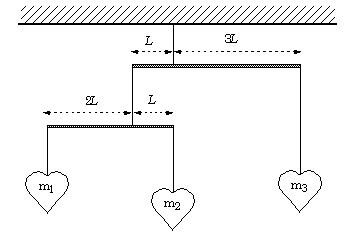
6. VFO 11 vraag 21: De
mobiel in onderstaande figuur bestaat uit hartjes die met touwtjes aan dunne
horizontale latjes zijn bevestigd. Het geheel is in evenwicht.
Verwaarloos het gewicht van de touwtjes en de
latjes.
Over de hartjes mag je het volgende zeggen:
m1>m3>m2
m1<m3=m2
m1=m3<m2
geen van bovenstaande beweringen is correct
7. Een
cilinder staat op een horizontale draaitafel op 0,20 m van het middelpunt. De
wrijvingsfactor (wrijvingscoŽfficiŽnt) tussen de tafel en de cilinder bedraagt
0,20.

Wat kan men zeggen over de maximale snelheid die de cilinder
langs de cirkelvormige baan kan hebben alvorens weg te glijden van de
draaitafel?
0,00 m/s < v < 0,50 m/s
0,50 m/s < v < 1,00 m/s
1,00 m/s < v < 1,50 m/s
1,50 m/s < v < 2,00 m/s
8. Een plastic
ballon met een massa van 25,5 g wordt gevuld met He tot wanneer het volume 50
liter bedraagt. Aan de ballon hangt een touw. De massa van 1 meter touw bedraagt
15 g.
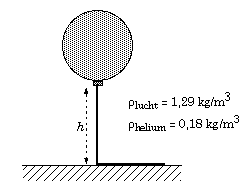
Deze ballon stijgt op in de lucht tot er h meter touw van de
grond opgetild is.
h is:
1,0 m
1,5 m
2,0 m
2,5 m
9. Een recipiŽnt
R gevuld met vloeistof wordt gewogen met behulp van een elektronische balans B.
De balans staat op een laboratoriumtafeltje, waarvan de hoogte h kan veranderd
worden met de stelschroef S.
Een kogel K, bevestigd aan een touw, wordt opgehangen met
behulp van een statief St.
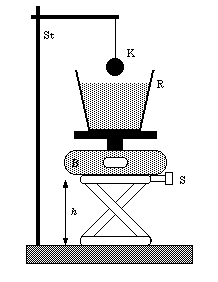
Als het laboratoriumtafeltje naar omhoog wordt gedraaid tot
de kogel helemaal is ondergedompeld in de vloeistof dan:
zal de aflezing van de balans toenemen.
zal de aflezing van de balans onveranderd blijven.
zal de aflezing van de balans afnemen.
kunnen we, wegens gebrek aan gegevens, niet zeggen of de aflezing op de balans toeneemt, onveranderd
blijft of afneemt.
10. Twee
voorwerpen ( m = 10,0 kg en M = 15,0 kg) zijn verbonden met een niet uitrekbaar
massaloos touw (zie figuur) dat breekt als de spankracht groter is dan 145 N.
Het systeem vertrekt vanuit stilstand. De versnelling is 2,00
m/s≤ zolang het touw niet breekt.

De spankracht in het touw is dan gelijk aan:
100 N
120 N
140 N
De vraag heeft geen zin want het touw breekt