Some puzzles

This page has many puzzles most of which are sent to me by my friends. Most of them need only high school math.

1.(*1/2) A census agent goes to a house to enquire about the family and asks the head of the family about how many children he has and what are their ages. The head of the family says he has 3 children and says the product of their ages is 36 and sum of their ages is equal to their door number. The agent goes out to have a loot at the door number and comes back asking for another clue. The head then says. "my eldest son is sleeping in the next room". The agent finds the ages. Can you tell what are the ages ? Source : I don't remember. Added on 18th Nov 2001


2. (*1/2)In a hotel, there are 1000 rooms and 1000 room service men. Every morning the first service man opens all the rooms, then second service man closes every second room, then third service man closes if open, and opens if close i.e., toggles every third room and similarly, the nth service man toggles every nth room. The question is by the time all service men finished their work how many rooms are open and what are their room numbers ? Source : Bikash Kumar Dey Added on 18th Nov 2001


3. (**)Suppose you have 3 coins and you place them in a triangular shape (i.e., two rows of coins with one row having one coin and the other have two coins) such that one of the corners is pointed towards you. By moving only one coin you can make one of the corners pointed away from you. Similarly, if you had 6 coins you need to move only 2 coins to change the orientation of the triangle (three rows with one rowhaving one coin, second row having two coins, third row having three coins). Now, suppose you have N rows of coins, with kth row having k coins, where k is from 1 to N. What is the minimum number of coins you have to move to change the orientation of triagle by 180 degrees ? --- Source : Through internet Added on 20th Nov 2001


4. (**1/2)What is the maximum number of areas you can cut a plane into, using N straight lines ? For example, you can cut a plane into two areas at most using 1 line, and into four at most using 2 lines, and into seven areas at most using 3 lines. ---- Source : Friends discussion (Bikash, Arun and me) Added on 30th Nov 2001


5. (***)What is the maximum number of volumes you can cut a space into, using N planes ? (An extension of the above problem) ---- Source : Generalization of the above Added on 30th Nov 2001


6. (****)There is an island with 100 people on it. 50 of them have red eyes and the remaining have green eyes. They have a belief that if a person with green eyes dies, then he will go to heaven. And it is a fact that a person would die happily to go to heaven. So, if a person knows that he has green eyes then he will die the day he knew it. But the problem is they don't have any sort communication between them. They don't have mirrors or any reflection surface to see their faces. So, if a person has to know about his eyes, he has to know it by himself. These people are very intelligent. The question, will the persons with green eyes be able to find that they have green eyes and then die ? If so, when will they die ?---- Source : Bikash Kumar Dey Added on 5th Dec 2001


7. (***1/2)There is a grid of M by N dots. You are asked to touch all the points in a single path of straight lines. You can go outside the M by N grid and cross the path. Now the problem is : what is the minimum number of straight lines the path can have ? ------ Source : Bikash Kumar Dey from IT newsletters I guess, everyone is familiar with the 3 by 3 version of this problem. The answer for 3 by 3 is 4, as shown in the following figure.
Added on 21st Dec 2001


8. (***1/2)Let S be a finite set of points in 2-d plane, in which for every two points x and y in S, there exists z in S, such that x,y,z are collinear. Prove that S is collinear. -------- Source : Anil Kumar Added on 7th Jan 2002


9. (****)Suppose you have a rectange A partitioned to many small rectangles such that the sides of any small rectangle are parallel to the sides of the rectangle A. Prove that, if every small rectangle has at least one integer side then the rectangle A also has an integer side. ------ Source : I don't remember. Added on 7th Jan 2002


10. (**1/2)Suppose you have a chocholate bar with M rows and N columns and you are asked to distribute it to MN people, equally. What is the minimum number of times you have to break the chocholate bar ? The rule is that you can break only one piece at a time. ------Source : CSA interview at IISc Added on 20th Jan 2002


11. (***)Suppose there is a M x N rectangular grid. How many possible paths are there from the top left corner to the bottom right corner ? Note : A path here is a sequence of connected straight lines which doesn't intersect itself and always goes to right or down. ---- Source : CSA interview at IISc Added on 20th Jan 2002


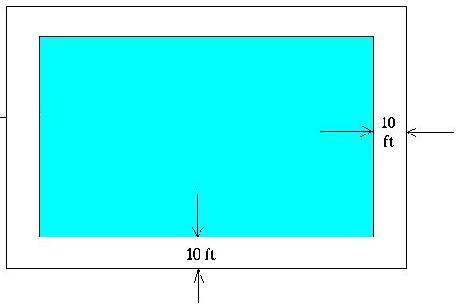
12. (**)There is rectangular fort around which there is a moat, as shown in the following figure. You have two wooden planks, each of length "x" and you don't have any means of attaching these two planks. Can you cross the moat if x is less than 10ft ? If so how and what can be the minimum possible value of x in that case ? ----- Source : I don't remember the book I read it from.
Added on 2nd Feb 2002


13. (*)Suppose you have two mugs, one with M litres capacity and the other with N litres capacity. What are all the possible values of X, such that you can measure X litres of milk using these two mugs ? ----- Source : None Added on 13th Mar 2002


14. (*)There are ten packets of ten pens each. In every packet the weight of each pen is 100 grams except in one packet X. In the packet X, the weight of each pen is 10 grams different from the pens in other packets. You have a spring balance and you are asked to use it only once. Find which packet has different weight pens and what is the weight of each pen in that packet ? ---- Source : Mallikarjuna Rao Added on 8thth Mar 2002


15. (***1/2)There are 8 balls, all of which are similar in shape and size. Seven of them have same weight too. You are asked to use two-sided balance three times only and find which ball has different weight and is it less than the other balls or more than other balls ? ---- Source : Bikash Kumar Dey Added on 22nd Mar 2002


<16> (***1/2)Try the above problem with 12 balls instead of 8 balls. What if it is 13 balls ?


17. (**)A 3 x 3 x 3 cube contains 27 1 x 1 x 1 cubes in it (something like Rubick's cube). An ant starts at any corner of the big cube and travels only on the edges of the small cubes. Can the ant cover all the small cubes exactly once and end up in the middle ? If so, give the path. Otherwise why ? --- Source : I don't remember the book I read it from. Added on 5th Apr 2002


18. (*1/2)A room is of 10 x 10 x 10 m^3 dimensions. An ant has to travel from one corner of the room to the opposite corner of the room. It can't fly and only can walk. Suggest the ant the shortest possible path between the opposite corners. --- Source: from my high school. Added on 5th Apr 2002


19. (*)I am twice as old as you were, when I was as old as you are. What is my age and your age ? --- Source : from my high school. Added on 11th Apr 2002


20. (*1/2)There are five chains each with 3 rings. What is the minimum number of rings do you have to cut in order to join all of them and make a chain with 15 rings ? --- Source : Some aptitude test paper. Added on 18th Apr 2002


21. (****)Let a, b be two integers between 1 and 50 (both excluding). Two persons (both of them know that the numbers a, b are from 2 to 49) P and S, know the product ab and sum a+b respectively. Now, P says to S : I have no idea what the sum is and what the numbers are. S says to P : I know that you have no idea about them. P says to S : I know the sum and the numbers now. S says to P : I too know the numbers now. So what are a anb b ? ---- Source : Indranath Sengupta Added on 14th May 2002


22. (***1/2)How many rectangles are there on a chess board ? In general, how many rectangles are there on a N x M chessboard. Added on 23rd May 2002


23. (***)A wolf is waiting for you on the circumference of a perfectly circular pond. You are sitting on rock in the middle of the pond. The wolf can move four times the speed at which you can swim, but if you can reach the bank in front of the wolf, you can outrun him, assuming you run faster than the worf. Can you escape from wolf and get out of the pond and, if so, how? What if the wolf can move five times faster than you can swim ? ---- Source : Some puzzle book. Added on 11th Jun 2002


24. (**1/2)Given any nine points in a unit square, is there a triangle among the triangles having vertices on the given points at least one whose area is less than or equal to 1/8 ? What if the number of points was N ? ---- Source: Mallikarjuna Rao. Added on 11th Jul 2002


25. (***)A n-sided regular polygon is a polygon which looks same from any corner and any edge. Similarly a regular polyhedran (3-D object) is a polyhedran which looks the same from any corner and any edge and any face. Its a well known fact that there are only 5 regular polyhedrons known as platonic solids. Prove this. Source : none Added on 25th Jul 2002


26. (***)Prove that a cube can be unfolded into a two dimensional surface in 11 ways (i.e., you can cut a paper into 11 shapes such that each shape can be folded to form a cube). Source : some magazine Extension : What if the regular polyhedron is not a cube but one of the any other four ? Added on 25th Jul 2002


27. (***)The beads in a chain of black and white beads are to be shared between two friends. The number of black beads and white beads are both even. What is the maximum number of cuts necessary such that both the friends get same number of black beads and same number of white beads. Source : some magazine Added on 6th Aug 2002


28. (**** Let ABC be a triangle and let D,E and F be points on the sides AB,BC and CA respectively, such that AD=BE=CF. Prove that if the triangle DEF is equilateral then so is triangle ABC.Added on 15th Apr 2003


29. (**) On a square of 10 km side, four dogs are on the four corners of the square. With a speed of 1km per second, each dog starts chasing the dog on its left, always directed along the line joining them. What is the time taken by each dog to catch the dog on its left. ---- Source :High school physicsAdded on 15th Aug 2003


30. (**1/2) On a square of 1km side, four dogs are standing on the four corners of the square. Each dog starts chasing the dog to its left with a speed of 100 meters per second and is always directed to the dog it chases. What is the time taken by each dog and what distance each dog travel ?


31. (***) In a tournament, N teams take part. Team A gets a gold medal if either the team A defeats all the other teams or for every team B which defeated A, there exits a team C such that C defeated B and A defeated C. What are the values of N such that all the teams get a gold medal ? Clearly, if N=3, then A defeats B defeats C defeats A and hence all get a gold medal. Added on 15th Apr 2002


32. (***)Let {x(1)< x(2)< x(3)<...< x(n)}U{y(1)>y(2)>y(3)>...>y(n)} = [1,2n], where n is a natural number. Then prove that |x(1)-y(1)| + |x(2)-y(2)| + |x(3)-y(3)| + ... + |x(n)-y(n)| = n^2. --------- Source : Mallikarjuna Rao


33. (***1/2)A rope which takes 1 hour to burn completely at a non-uniform rate is given to you. Can you measure 30 minutes using this rope ? If so how ? Using such two ropes can you measure 45 minutes ? If so how ? Otherwise why not? Using such one rope can you measure 15 minutes ? If so how ? Otherwise why not?


34. (**1/2)Using each of the 3,3,8,8 exactly once and any of the operations +,-,*,/ obtain 24. Remember that only these four operations are allowed. No powers, factorials etc. Also remember that no adjoining them like 38 or 88 etc. ------------- Source : Times of India Mindsport page.


35. (*1/2)Four guys come across a rope bridge which can take at most 2 people on it and it is very dark. And they have a torch whose batteries come for another 17 minutes. All the four guys walk at different speeds. One of them takes 10 minutes to cross the brigde, the second one takes 5 minutes, the third one takes 2 minutes and the last one takes 1 minute. How do they cross the bridge before the torch goes off ?


36. (1/2)What is the probability that two of the three persons in a room are of same sex ? ------------ Source : Own


37. (*1/2)Prove that there exists a subset in a set of any n integers such that the sum of the integers in the subset is divisible by n, for any n. ---------Source :Some putnam or INMO


38. (*1/2)Find all the pairs of positive integers (a,b) such that S(a+x)=S(b+x) for all integers x with a+x,b+x > 0 and S() denotes the sum of digits recursively. For example S(158) = S(1+5+8) = S(14) = 5.


39. (*1/2) Prove that a 10 digit number with one 1, two 2s, three 3s and four 4s cannot be a perfect square.