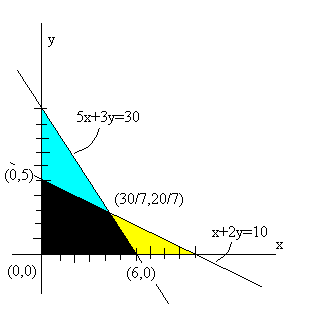Linear inequalities

Systems of linear inequalities

One linear inequality

Convert the inequality to an equation and plot the line.
Choose a test point to decide which half of the plane satisfies the inequality.

Example: Shade the region bounded by the inequality 2x + 3y ³ 6.

First sketch the line 2x + 3y = 6.
x | y
-----
0 | 2
3 | 0

The line splits the x-y plane into two halves. One half is 2x + 3y ³ 6 and the other is 2x + 3y £ 6. To decide which half to shade substitute in the point (0,0) and note that 2(0) + 3(0) £ 6. Hence the origin which lies below the line is in the wrong region. So shade the region above the line. Linear inequality

System of inequalities

Apply the above procedure to each inequality.
Be sure to find all the corners or verticies of the region.
Find the intersection of the regions obtained from each inequality.

Example: Shade the region bounded by

æ  x + 2y  ³  10 ö
ç 5x + 3y  ³  30 ÷
ç  x  ³  0       ÷
è  y  ³  0       ø

Sketch the line x + 2y = 10 and shade the region yellow.
x  | y
------
0  | 5
10 | 0
Sketch the line 5x + 3y = 30 and shade the region blue.
x | y
------
0 | 10
6 | 0
Shade the intersection of the regions black.
Find the intersection of the two lines.

é  1  2 | 10  ù
ë  5  3 | 30  û

 
 R₂   > R₂ - 5 R₁

é  1  2 | 10  ù
ë  0 -7 |-20  û

y = 20/7
x + 2(20/7) = 10, x = 30/7
The intersection is (30/7,20/7).

Exercises

(1) Shade the region 2x + y £ 4. Graph of linear inequalities.

 a)
 b) 
 c)
 d)

(2) Shade the region

æ 3x + 6y  ³  12 ö
ç -x + 2y  ³  4  ÷
ç  x  ³  0       ÷
è  y  ³  0       ø

 a)
 b) 
 c)
 d)