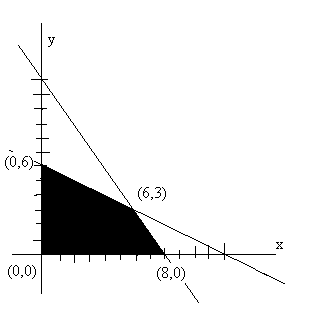Method of corners

In the previous example the function P = 10x + 12y is called the objective function and the system of inequalities 

æ  x + 2y  £  12 ö
ç 3x + 2y  £  24 ÷
ç       x  ³  0  ÷
è       y  ³  0  ø
forms a region in the x-y plane known as the feasible set. The method of corners is a graphical method for finding the point in the feasible set which maximizes or minimizes the objective function and is summarized in the following steps.
  1. Graph the feasible set
  2. Find all the corners of the feasible set.
  3. Evaluate the objective function at each of the corner points.
  4. Find the corner which maximizes or minimizes the objective function.
    If two adjacent corners both optimize the objective function, then there are infinitely many solutions along the line segment joining the corners.

Example:     Maximize P = 10x + 12y subject to the constraints 
æ  x + 2y  £  12 ö
ç 3x + 2y  £  24 ÷
ç       x  ³  0  ÷
è       y  ³  0  ø

(1) FIND THE FEASIBLE SET 

Sketch the line x + 2y = 12 and shade the region yellow.
x  | y
------
0  | 6
12 | 0
Sketch the line 3x + 2y = 24 and shade the region blue.
x | y
------
0 | 12
8 | 0
Shade the intersection of the regions black.
Find the intersection of the two lines.

é  1  2 | 12  ù
ë  3  2 | 24  û

 R2   > R2 - 3 R1
 
é  1  2 | 12  ù
ë  0 -4 |-12  û

y = 3
x + 2(3) = 12, x = 6
The intersection is (6,3).
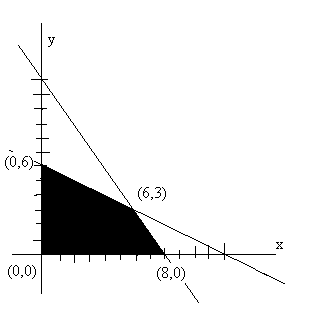
Linear inequalities 
(2) EVALUATE THE OBJECTIVE FUNCTION AT EACH OF THE CORNERS 

P(0,0) = 10(0) + 12(0) = 0
P(8,0) = 10(8) + 12(0) = 80
P(6,3) = 10(6) + 12(3) = 96
P(0,6) = 10(0) + 12(6) = 72

(3) FIND THE CORNER WHICH MAXIMIZES THE OBJECTIVE FUNCTION 

Maximum profit of $96 
x = 6 bags of product A
y = 3 bags of product B

Exercise 

(1) Minimize C = 3x + 4y
subject to the constraints
æ  x + 3y  ³  15 ö
ç 4x +  y  ³  16 ÷
ç       x  ³  0  ÷
è       y  ³  0  ø

 Hint
 x = 15, y = 0 and C = 45
 x = 0, y = 16 and C = 64
 x = 3, y = 4 and C = 25

| Table of Contents | | Previous | | Next |