Solution Types

Solution types

Geometrically, it is clear that there are three possibilities for the solution of two linear equations in two unknowns
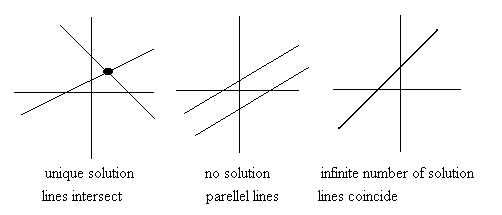
Solution types
The same possibilities hold for systems of three or more equations.

Example: Solve

æ x + 2y - 3z = -2 ö ç 3x - y - 2z = 1 ÷ è 2x + 3y - 5z = 3 ø

é 1 2 -3 | -2 ù ê 3 -1 -2 | 1 ú ë 2 3 -5 | 3 û

R₂ > R₂ - 3 R₁
R₃ > R₃ - 2 R₁

Eliminate the entries below the the first diagonal entry. The required multipliers are 3/1 = 3 and 2/1 = 2. The calculations leading to a new row 2 are 3-3(1) = 0, -1-3(2) = -7, -2-3(-3) = 7, 1-3(-2) = 7. The calculations leading to a new row 3 are 2-2(1) = 0, 3-2(2) = -1, -5-2(-3) = 1, 3-2(-2) = 7.

é 1 2 -3 |-2 ù ê 0 -7 7 | 7 ú ë 0 -1 1 | 7 û

R₂ > R₂/-7

Simplify the second row by dividing by -7.

é 1 2 -3 |-2 ù ê 0 1 -1 |-1 ú ë 0 -1 1 | 7 û

R₃ > R₃ + R₂

Eliminate the entry below the second diagonal entry. The multiplier is -1/1 = -1 and the calculationsleading to a new row 3 are 0+0 = 0, -1+1 = 0, 1+(-1) = 0, 7+(-1) = 6

é 1 2 -3 |-2 ù æ x + 2y - 3z = -2 ö ê 0 1 -1 |-1 ú OR ç y - z = -1 ÷ ë 0 0 0 | 6 û è 0z = 6 ø

Solve the new system using back substitution. Since the third equation 0z = 6 is impossible the original system has no solution.

Example: Solve

æ x + 2y - 3z = -2 ö ç 3x - y - 2z = 1 ÷ è 2x + 3y - 5z = -3 ø

é 1 2 -3 | -2 ù ê 3 -1 -2 | 1 ú ë 2 3 -5 | -3 û

R₂ > R₂ - 3 R₁
R₃ > R₃ - 2 R₁

Eliminate the entries below the the first diagonal entry. The required multipliers are 3/1 = 3 and 2/1 = 2. The calculations leading to a new row 2 are 3-3(1) = 0, -1-3(2) = -7, -2-3(-3) = 7, 1-3(-2) = 7. The calculations leading to a new row 3 are 2-2(1) = 0, 3-2(2) = -1, -5-2(-3) = 1, -3-2(-2) = 1.

é 1 2 -3 |-2 ù ê 0 -7 7 | 7 ú ë 0 -1 1 | 1 û

R₂ > R₂/-7

Simplify the second row by dividing by -7.

é 1 2 -3 |-2 ù ê 0 1 -1 |-1 ú ë 0 -1 1 | 1 û

R₃ > R₃ + R₂

Eliminate the entry below the second diagonal entry. The multiplier is -1/1 = -1 and the calculations leading to a new row 3 are 0+1(0) = 0, -1 +1(1) = 0, 1+1(-1) = 0, 1+1(-1) = 0.

é 1 2 -3 |-2 ù æ x + 2y - 3z = -2 ö ê 0 1 -1 | 1 ú OR ç y - z = -1 ÷ ë 0 0 0 | 0 û è 0z = 0 ø

Solve the new system using back substitution. Notice that in the third equation 0z = 0 it is possible z to be any number. We then solve for x and y in terms of z. y - z = -1, y = z - 1 x + 2y - 3z = -2, x + 2(z-1) - 3z = -2, x - z = 0, x = z Hence, we have an infinite number of solutions of the form

æ x = z ö ç y = z -1 ÷ è z = any number ø

Exercises

(1) Solve

æ  2x - 3y =  5  ö
è -4x + 6y = -10 ø

 x = 4, y = 1
 Infinite number of solutions of the form x = (5 + 3y)/2, y = any number.
 No solution.

(2) Solve

æ  2x - 3y =  4  ö
è -4x + 6y = -10 ø

 x = 5, y = 2
 Infinite number of solutions of the form x = (4 + 3y)/2, y = any number.
 No solution.

(3) The figure below shows the traffic flow on a city block. The arrows indicate the direction of traffic flow. Set up and solve the system of linear equations governing traffic flow.

 Little hint.
 Big hint.
 Answer.