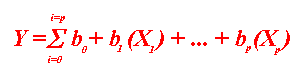
02-17-98
This is a really BIG subject. In its most innocent guise, it deals with how you specify the dependent variable in a GENERAL LINEAR MODEL. In this context, we're talking about a numerical variable that we are either trying to PREDICT or EXPLAIN on the basis of other INDEPENDENT VARIABLES.
In a BROADER sense it refers to how you define the OBJECTIVE FUNCTION in a modeling situation where you are either trying to MAXIMIZE or MINIMIZE the dependent variable for the OBJECTIVE FUNCTION.
The choice of an appropriate DEPENDENT VARIABLE is important in both a predictive context (SEE DATELINE 01/03/98 PREDICTIONS and PROGNOSTICATIONS: NEWSLETTER) and a context involving empirical testing (SEE: EXPERIMENTAL DESIGN).
In either case, the first REQUIREMENT for MINIMAL PROPER ANALYSIS is that the DEPENDENT variable is a continuous RATIO or INTERVAL scaled numerical variable. A weaker compromise would be that the DEPENDENT VARIABLE can either be rank ordered or measured an a YES or NO (0, 1) basis. In either case, it MUST be amenable to NUMERICAL ANALYISIS. The single most important aspect is that the dependent variable is MEASURABLE, and represents that which we are trying to predict or explain rather than being one of the predictors.
This is not REALLY TOO MUCH TO ASK. Nevertheless, consider that many policy decisions are made on the basis of nothing more than anecdotal evidence, which does not meet even these modest requirements.
Let's assume that numerical encoding is not a problem. Does it all end here? Not by a long shot. Even if the DEPENDENT variable is NUMERICAL, there are problems in MISSPECIFICATION that neither the MEDIA nor ORDINARY citizens seem to be aware of or care about. A case in point is:
The educational establishment has a penchant for encouraging the public to confuse MEANS (i.e. SPENDING on EDUCATION) for RESULTS. Let's assume that a proper and unambiguous RESULTS oriented measure of EDUCATIONAL EXCELLENCE is not INPUT (SPENDING) but output (SAT SCORES or other standardized measures).
An interesting exercise that you can try out yourself is to take all 50 states and for the most recent year where such figures are available, first rank the states on the average SAT scores for each state. Now form a second column by ranking the same 50 states on PUBLIC (TAXPAYER) SPENDING on EDUCATION per STUDENT in GRAMMAR SCHOOL and HIGH SCHOOL. Then compute the RANK ORDER CORRELATION between the two sets of ranks. What you'll find is a SPEARMAN's RANK ORDER CORRELATION RHO (non-parametric, since we're using ranks) in the neighborhood of [-.5].
To see how you can run this example on your own computer, look at the UNDER THE HOOD... COMPUTATIONAL DETAILS section of this posting to see how APL can perform the computational grunt work using a single line of code.
In any event, what this negative correlation suggests is that whenever we INCREASE spending per pupil, the statistical expectation is that average SAT scores will DECREASE. Of course, it could also mean that we are throwing good money after bad. The worse the performance, the more we reward it by throwing more money at it.
Specifying the proper dependent variable is another way of saying that we need to understand which variable is the CAUSE and which is the EFFECT. A measure of association such as a correlation coefficient won't help us here. Even if there is a non-trivial association between two variables, a correlation won't tell you which variable CAUSES which other variable to change (i.e. is additional spending a CAUSE or EFFECT of lower performance scores in education; does the rooster CAUSE the sun to rise or vice versa; is CO2 a CAUSE or EFFECT of global warming... etc.).
Deeper study will be required. More than two variables will also be likely to play a role. Sometimes the REAL causal variable is ignored while the correlations or associations between two 'effect variables' are studied.
While the 'spending vs. performance' example from the field of education is one of those "Don't believe it .... but don't ignore it either." factoids since we only have rank order data, it certainly should cause us to question the wisdom of using SPENDING as a measure of educational QUALITY/ATTAINMENT, and thus as a DEPENDENT VARIABLE.
There are undoubtedly many other instances of misspecifying the DEPENDENT VARIABLE by confusing ENDS with MEANS. You can probably think of some yourself.
04-24-07
It's now later and here's more.
The education example above used the Spearman Rank order coefficient as a measure of association. The formula for this is as follows:
SpearmanRho = 1-((6*SUM di2)/(n3-n))
What follows is a brief example using seven pairs of arbitrary data points, of how a rank order correlation coefficient (Spearman's RHO) can be computed by an APL 'one liner':
The Y and X vectors are raw data. The APL function transforms them to ranks and then computes the rank order correlation coefficient. The preceding topic was mainly about a Bi-Variate non-parametric measure of Association with data which was rank ordered rather than interval or ratio scaled.
More often than not in Real World situations, we'll be dealing with more than just one independent variable, and the variables will be interval or ratio scaled. We'll therefore need Multiple rather than Bi-Variate measures of Association/Regression. This provides not only a model which allows us to predict the Dependent Variable on the basis of the values of one or more Independent Variables, but also gives us some hints as to the relative importance of each Independent Variable in the prediction. Here's how Multiple Regression looks in MATRIX ALGEBRA:
Beta = (X'X)-1 X'Y
The X represents a matrix of independent variables where the the rows are observations and the columns are the variables. The first column consists of all 1's. This augmentation is necessary for the computation of the constant term. The Y represents a vector containing the values of the Dependent Variable for each observation.
Beta is the vector of regression coefficients that result from solving the regression problem. The first term in the equation is the inverse of the X matrix multiplied by its transpose. This is in turn multiplied (inner product matrix multiplication) by the matrix product of the transpose of X and the vector of the Dependent Variable Y.
It's possible to transcribe Matrix Algebra almost verbatim into an array processing language such as APL. The challenge in APL is to get everything on a single line.
Here's a close to literal transcription of the matrix equation into APL:
By APL standards, this particular expression is klunkier and less elegant than is considered to be good form. The excessive parentheses are there mainly because we keep repeating the transpose of X and X augmented by a vector of 1's, i.e. (1,X). We've kept it this way to replicate the MATRIX ALGEBRA formulation as closely as possible.
A much more concise expression that performs the same calculations looks like this:
We've called this version REG2 to distinguish it from the first version, but it does exactly the same thing as REG and gives exactly the same answer. What's useful about this APL function is that in an APL workspace, you can plug in data and run it through this 'one liner' function and get numerical results.
You can assign actual values to Y and X and then type
Y REG X or alternately Y REG2 X
and get a display of the coefficients. In the preceding example, there are only two independent variables. The first of the displayed coefficients is the constant while the last two are are coefficients for each of the two variables.
Slightly longer versions of the Regression function are available, which include all the statistical information that goes along with Multiple Regression (ANOVA table, Multiple R and R2, Significance of each coefficient etc.).
There are several ways to implement such computations on your own computer. Link to our Array Processing Resources page to find out more.
(SEE: ARRAY PROCESSING RESOURCES)

o Return to: 'SPRING SYSTEMS HOME PAGE'