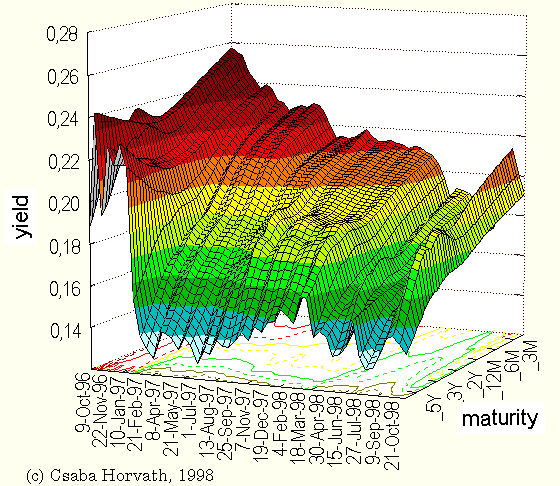
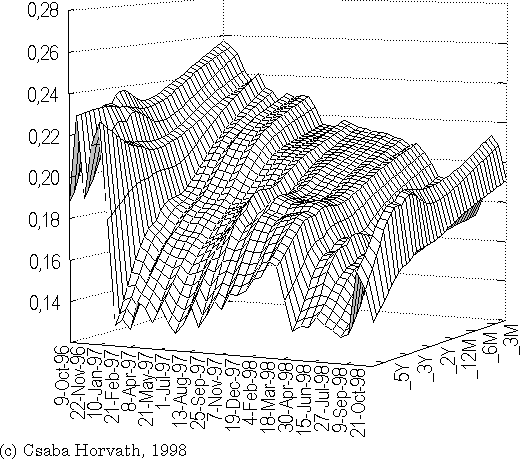
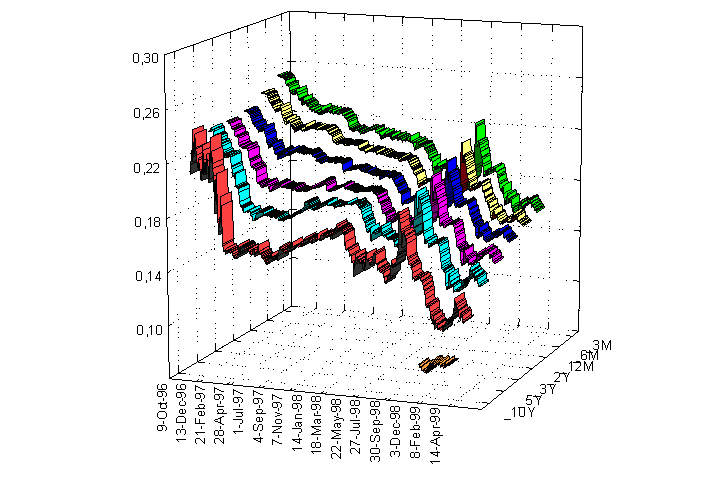
November 9, 1996 - April 28, 1999

Estimated by the ZCalc zero coupon yield curve estimation software.

Svensson (extended Nelson-Siegel) method was used, based upon the REUTERS quotations (page HUBEST1..HUBEST3). Maturities are: 3, 6 months, 1,2,3,5 and 10 years (from right to left on the graph, that is the curve is downward-sloping due to a deflationary process).

The longest T-note (and hence the estimated curve itself) has a maximum maturity of 5 years until January 19th, 1999 and up to 10 years from that time on. The longest T-bill has only a one-year maturity.

Historical zero coupon yield curve, Hungary, 11-Nov-96 – 1-Dec-98

Historical zero coupon yield curve, Hungary, 11-Nov-96 – 28-Apr-99