Let us consider
all the events of a Minkowski space-time in which the four coordinates
t,
x, y, z, are integers, and the velocity of light
C is chosen as an unit. These events form a hypercubic lattice.
The null lines joining the
event points of the lattice derive from Lorentz transformations which make
the lattice an invariant set. We will call those lines
“integral null lines”, and the transformations “Lorentz integral
transformations”.
The contemporaneous time
lines which are traced on the lines parallel to the axis of time
T by Lorentz integral transformations, will be called time integral lines.
Let us construct, therefore,
the model of this Schild*discrete
space-time as a lattice made by discrete moduli
of lenght L. The
elementary discrete length L is considered as the smallest non-null
space interval among the event points of the lattice.
The integral time lines are
to their turn composed by moduli of discrete time T considered as
the smallest non-null time interval among
the event points of the lattice.
In the Schild discrete space-time,
the dimensional quanta of time T can have a certain kind of dimensional
elasticity, and their value can locally vary in any zone of the lattice,
constituting a variation in the temporal uniformity of the hypercubic
lattice.
In this work, the space–time
pertubations of the lattice structure are supposed to propagate in the lattice
itself, while their motion is supposed to consist in a regular temporal sequence
of points inside the lattice in order to bind the following points with null
integral lines and temporal integral lines.
The propagation velocities
of the pertubations of the lattice are the ratios between space and time
quanta of the lattice, and they are associated with the integral Lorentz
transformations described by the components t,x,y,z, of primitive
integral vectors that must fulfill the diophantine equation:
1)
( t2
- x2 - y2
- z2) = 1
Thanks to it we attain the velocities:
2) 
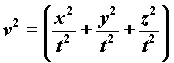
It follows that:
3)
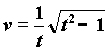
If we consider the dimensional quantum L as invariant, we are
forced to admit that the only variant quantum is the temporal quantum T.
All of that involves an unequivocal choice of the possible values for the
velocities associated with the integral time lines.
The time has two limit cases:
1) considering t = 2,
the lowest possible velocity for a pertubation of the lattice is given by:
4) 
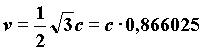
2) for t tending to
infinity, the maximum attainable velocity V tends to C.
In the lattice the first condition describes a pertubation of maximum
local deformation of the lattice, which propagates from a zone of the lattice
where is the temporal equivalent of a 3° hyperbolic space. This zone is made by points lying on the coherent sphere of maximum
curvature, and its equation is
1).
This zone is subjected to the maximum dimensional variation in time
quanta T which Schild says to be given by:
5) 
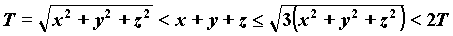
The second limit case describes the velocity of pertubation V
tending to C for t tending to infinity, which moves in an
almost plane lattice having a minimum curvature, and therefore a great
but still not infinite radius.
FIG.1
In the first case, we consider the temporal perturbations of the lattice
as geometrical variations of the moduli of lenght L which have,
on the contrary, a constant lenght as in the second case. This lenght verifies
the limit of the curvature condition for an infinite radius.
Perturbation fronts which behave like plane wavefronts in the lattice,
entering the field of curvature of spherical wavefronts, move in the lattice
according to the dimensional characteristics they meet in the spherical
space-time established by the pre-existent spherical perturbations.
When the spherical perturbations are locally and periodically induced
(we will see later a plausible model) a field of spherical waves develops
and its curvature can influence the propagation direction of the perturbation
surfaces introduced in the space- time of its existence.
*Alfred
Schild --Physical Review 1948. Vol. 73, pag. 414-415
Alfred Schild
-- Canadian Journal of Mathematics 1948, pag. 29-47
