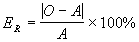
Error Analysis
Physics concepts are revealed through the collection and analysis of numerical data that quantify an event. Since this data is collected through human endeavors it is impossible to eliminate all the possible sources of error that may occur in its collection. Therefore, it becomes necessary to make a quantitative determination as to the amount of error that was incurred in the collection of data.
To report the amount of error contained in a collection of data, one may calculate the relative error (Er), also known as percent error; or one may calculate the relative deviation (Dr), also known as percent difference.
Percent Error:
The percent error is actually a determination of the accuracy of measured data. It informs the reader of how close a measurement has come to accepted value for the quantity measured. The percent error can only be calculated when the experimenter knows an actual or accepted value for a quantity.
The equation to calculate percent error:
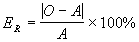
where: "O" is the observed or measured value for a quantity and "A" is the accepted value for a quantity.
Example: Jeff is known to be 6'1" (73 inches) tall; however Brad measures his height to be 6'3" (75 inches). Calculate the percent error of Brad's measurement.
|
ER = ? |
ER = |O - A| / A X 100% |
|
O = 75 in |
ER = |75 in - 73 in| / 73 in X 100% |
|
A = 73 in |
ER = 0.027 X 100% |
|
ER = 2.7% |
Percent Difference:
Percent difference is actually a determination of the precision found in a collection of measurements. It is calculated when an actual or accepted value for a given quantity is unknown. It represents the agreement among several measurements of a quantity taken in a similar fashion. The idea being that if several measurements of the quantity tends to closely agree with each other, there is a better chance that the measured numerical data approaches the accepted value. As this definition implies, precision has absolutely nothing to do with correctness. Precision indicates the degree of exactness or how fine a measurement is being made.
The equation to calculate percent difference:
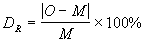
where, "O" is an observed or measured value for a quantity and "M" is the mean(average) of the set of measured values.
Example: Jeff does not know how tall he is, but would like to find out. Three people measure his height. The first measures 6'1" (73 inches), the second measures 6'2" (74 inches), and a third measures 5'11" (71 inches). What is the relative deviation (percent difference) of the second measurement?
|
DR = ? |
DR = |O - M| / M X 100% |
|
O = 74 in |
DR = |74 in - 72.7 in| / 72.7 in X 100% |
|
M = 72.7 in |
DR = 0.018 X 100% |
|
DR = 1.8% |
Precision not only indicates the quality of the measurments being taken, but it can also indicate the quality of the measuring device being used to take the measurement. A measuring device has good precision if it provides for more detail when measuring. For example, a micrometer, capable of measuring to one millionth of a meter is more precise than a meter stick which is capable of measuring only to one thousandth of a meter.
Remember when taking a measurment, the measuring device is read to within a fraction of the smallest scaled division of the device.