The information below represents the mathematics you must be proficient in to solve the overwhelming majority of the problems you will encounter in this course. There will be some work with logarithms and Level 1 classes may touch upon calculus, but it will be very little.

 A. Algebra

1. Algebra involves solving problems for a specific variable.

2. This is done by ISOLATING the variable on one side of the equation.

3. The variable can be isolated by transforming all the other variables in the equation to the opposite side. This is done by performing the opposite mathematical operation of the variable in question to both sides of the equation.

4. Remember the order of operations in solving a problem:


          1) Parenthesis - Innermost first
          2) Exponents
          3) Multiplication/Division
          4) Addition/Subtracting

1. Trigonometry deals with the relations between angles and sides of triangles.

2. The 180 degree rule: The three angles of any triangle add up to 180 degrees. Therefore of 2 angles of a triangle or known the other can be calculated by simply subtracting the sum of the two given angles from 180.

3. A right triangle is one which contains a 90 degree angle.
   

             
1. We know that the other 2 angles add up to 90 degrees.
2. The side opposite of the right angle is termed the hypotenuse. The hypotenuse will always be the longest side of a right triangle.
3. The angles are labeled A, B, C with the hypotenuse being C
4. The side opposite angle A is labeled a.
5. The side opposite angle B is labeled b.
6. The side opposite angle C is labeled c.

4. A common geometric function that can be utilized for a right triangle is the Pythagorean Theorem. It states, "the square of the hypotenuse equals the sum of the squares of the other two sides."

c² = a² + b²

 

5. Three common functions of an angle are called

sine (sin)
cosine (cos)
tangent (tan)

6. For any angle q, (A,B, or C) these functions are expressed as:

a) sin q = opposite side / hypotenuse
b) cos q = adjacent side / hypotenuse
c) tan q = opposite side / adjacent side


7. Example and Illustration

Angle A in a right triangle is 30^O, the hypotenuse is 8.0 cm, what is the length of side b?



---

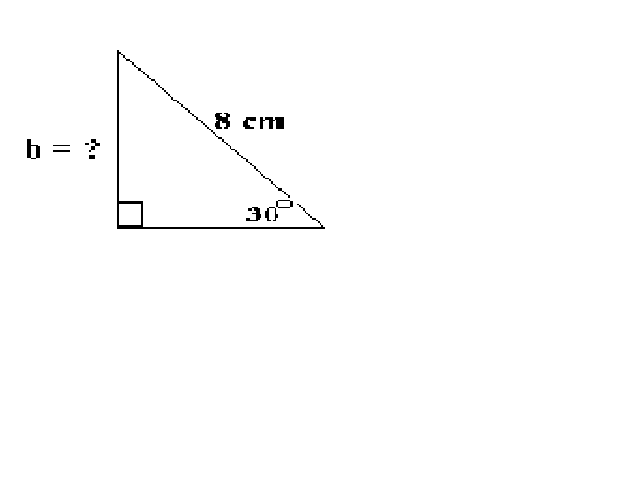
q = A = 30^O                           Cos q = adjacent (b) / hypotenuse (c)
C = 90^O                                    b = Cos q * c
c = 8.0 cm                                 b = Cos 30^O * 8.0 cm
b = ?                                          b = 6.9 cm
8. Note that the Law of Sines or the Law of Cosines may be helpful for some problems but the problems may be solved without applying these laws.