Physics

Vandebilt Catholic High School

W. Dupre

Work & Power – Notes

A. Work

1. Defined - the amount of force required to move an object against resistance or resistances for a given distance. For the sake of clarity, we should always refer to work in terms of work against a resistance.

2. The Criteria for determining if work against a resistance is being accomplished is:

a. A force must be applied.

b. An object must be displaced

c. The direction of the force and the displacement must be the same.

Positive work   -the displacement and the force are in the same direction (q = 0^O).

Negative work   - displacement and the force are in opposite directions (q =180^O). Friction does negative work (the frictional force acts in the direction opposite the motion).

No work - displacement and force are perpendicular (q = 90^O) to each other.

The moon orbiting the earth is an example of when a force is applied and there is no work done. In the figure below, the gravitational force acts inward (it is the source of the centripetal force) and the velocity of the moon is perpendicular to the gravitational force (or in a direction tangent to the circle or orbit). The moon's displacement is in the direction of the velocity vector, perpendicular to the gravitational force. Thus, there is no component of the gravitational force parallel to the displacement and the work done by the gravitational force is zero. Since the net work done by gravity is zero, the moon moves at constant speed.

Net work  - the net work done on an object determines its motion. If the net work is zero, the object moves at constant speed or is at rest. The object accelerates if the net work has a value other than zero.

3. In other words, work is done in physics when a force is applied to an object and there is a displacement parallel to the direction of the force. No work is done unless there is a displacement parallel to the direction of the force. The force doing the work could be a component of an applied force. It would be the component parallel to the displacement.

4. EQUATION: The base form of the equation is given below

W = Fd

Where “W” is work, “F” is Force, and “d” is distance

The image below shows a box being pulled by a constant force along a horizontal surface and moved a displacement d. The force is applied parallel to the surface. The amount of work done is given by

W = F d

The image below shows a box being pulled by a constant force along a horizontal surface and moved a displacement d. The force is applied at an angle q to the direction of displacement.

Only the component of the force (F cos q) parallel to the displacement does work in the direction of the displacement.

The amount of work done in such a case is given by the equation:

W = Fd cosq

Note: q is the angle formed between the direction of the force and the direction of the motion.

Work is a scalar quantity - it has only magnitude, although it is the product of 2 vectors. In such a case we say that work is the “dot” product of the vectors force and displacement. The “dot” product of 2 vectors will always be a scalar quantity. It is given by the general form:

For work it is:

where

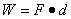
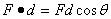
5. UNITS:

a) Joule

· the SI unit of work in the mks sytem.

· 1 J = 1 N m, or one Joule equals one Newton meter

· in mks units 1 J = 1 kg m² / s²

b) Foot-pound is the unit of work in the English system of measurement.

1 J = 0.738 ft-lbs.

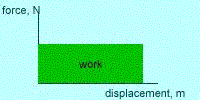
6. Work can be represented graphically. If you plot force vs displacement, the area under the curve represents the work done.

B. Work Done by a Varying Force:

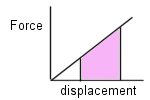
Graphical application: In the graph below, the force is changing. The graph shows how the force varies with displacement for an “ideal spring”. To determine the work done between the two points (the shaded area of the graph), one would simply need to find the area under the curve (or the area of the shaded area).

Calculus application:  Integration is used to find the area under a curve. If you integrate this curve, you have found the work done. This is useful when work is done by a varying force. The work done by a varying force in moving an object between two points is equal to the area under the curve between these two points. You will find the anti-derivative of the function, evaluate the anti-derivative for the final value of “x” and the initial value of “x”, and subtract the initial value from the final value. The result of these operations is the amount of work done by the force.

Example: Work done by a spring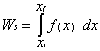

For example: if the force of a spring, given in newtons, varies with the position of the spring according to the function f(x) = 9x² + 2, how much work is done by the spring when the spring is displace from a position x = 2m to a position of x = 5m?

1. To begin write out the original integral:

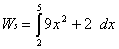
2. Take the anti-derivative of this function:

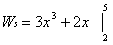
3. Evaluate the anti-derivative at 5 and 2 and subtract from each other.

W_s = [3(5³) + 2(5)] – [3(2³) + 2(2)]

W_s = [385] – [28]

W_s = 357 J

For an “ideal” spring:

therefore

C. Power

1. Definition – The rate of doing work.

2. Equation: P = W / t

where P is the power dissipated, W is the work done, and t is time in seconds

Since work is the product of force times displacement (W = Fd / t), power can also be expressed in terms of velocity (which is displacement divided by time).

P = F v

3. Units

a. Watts the SI unit of power

1 W = 1 J/ 1 sec, or one watt equals one joule per second

in mks 1 W = 1 kg m² / s³

b. Horsepower is the English unit for power. 1 hp = 746 W