O analiză a disputei

Vlad Enache

Cuprins

Preambul................................................................................................................... 5

Partea I – Discuţie................................................................................................ 6

Cadrul general............................................................................................. 6

Enunţuri şi atitudini. Definiţia discuţiei............................................................... 6

Fapte şi enunţuri. Păreri şi atitudini................................................................... 6

Atitudine şi comportament............................................................................... 7

Clasificarea atitudinilor.................................................................................... 8

Axa atitudinilor. Spaţiul atitudinilor................................................................... 8

Convenţii privind atitudinile. Tranziţie............................................................... 9

Spaţiul enunţurilor. Spaţiul enunţurilor acceptate............................................... 9

Tabelul de stare.............................................................................................. 10

Dispută............................................................................................................... 11

Apariţia disputei. Subiectul disputei................................................................. 11

Soluţie a disputei............................................................................................. 12

Victorie.......................................................................................................... 13

Dispute asociate. Pivot.................................................................................... 14

Concordanţe, discordanţe şi versiuni............................................................... 14

Reducerea unei asocieri de dispute la o dispută simplă..................................... 15

Pledoarie.......................................................................................................... 15

Definiţie.......................................................................................................... 15

Asimetrie. Avocat şi spectator......................................................................... 16

Soluţie a pledoariei......................................................................................... 16

Victorie.......................................................................................................... 17

Pledoarii asociate. Asocierea pledoarie‑dispută............................................... 18

Consens............................................................................................................. 18

Dinamica discuţiei........................................................................................ 19

Numai trei posibilităţi: dispută, pledoarie sau consens....................................... 19

Tranziţii în spaţiul atitudinilor............................................................................ 20

Totuşi, a patra posibilitate: dezbatere.............................................. 21

Încă un preopinent. Definiţia dezbaterii............................................................ 21

Componentele dezbaterii................................................................................. 22

Spaţiul tridimensional al atitudinilor.................................................................. 22

Soluţionarea dezbaterii.................................................................................... 23

Asocierea dezbaterii. Importanţa asocierii în general........................................ 23

A cincea posibilitate nu există............................................................. 24

Partea II – Argumentare.................................................................................. 26

Consideraţii preliminare......................................................................... 26

Motivele tranziţiei............................................................................................ 26

Nu există „arbitru”.......................................................................................... 26

Logică. Sisteme de ipoteze. Modele de judecată............................................. 27

Argument.......................................................................................................... 28

Atitudine logică............................................................................................... 28

Baza, structura şi concluzia argumentului.......................................................... 29

Mecansimul intern de funcţionare a argumentului. Structura‑p........................... 30

Implicaţii generale şi particulare....................................................................... 31

Argumentul merge de la general la particular.................................................... 31

Susţinere şi contra‑argument. Negaţie.............................................................. 31

Obiecţie. Contestaţie...................................................................................... 32

Motorul logic al argumentării........................................................... 33

Principiul general al argumentării...................................................................... 33

Contestaţia (sau obiecţia) nu poate fi contra‑argument..................................... 34

Baza falsă nu conduce la concluzie falsă................................................. 34

Nici structura falsă nu conduce la concluzie falsă..................................... 34

Distrugerea unui argument nu invalidează concluzia lui............................. 34

Combaterea unei susţineri............................................................................... 35

Argumentele în lumea reală.................................................................. 36

„Forţa” unui argument. Dificultăţi teoretice şi practice....................................... 36

Implicaţie şi negare. Insuficienţe ale limbajului.................................................. 37

Evitarea capcanelor limbajului......................................................................... 38

Nuanţarea implicaţiei şi a negaţiei ei................................................................. 38

Implicaţia şi relaţia cauză-efect........................................................................ 39

Confuzia cu echivalenţa. Altă insuficienţă a limbajului........................................ 39

De ce logică bipolară?............................................................................... 40

Limbajul este guvernat de logica bipolară......................................................... 40

Problemele logicilor nuanţate........................................................................... 40

Definiţie............................................................................................................. 41

Rolul definiţiei................................................................................................. 41

Definiţia nu poate fi falsă................................................................................. 42

*** Capitolele ce urmează sunt doar schiţate -----------------------------------------------

Ce este definiţia.............................................................................................. 43

Sinonimia........................................................................................................ 43

Omonimia....................................................................................................... 43

Tipuri de contestaţii................................................................................... 43

Reducerea la absurd....................................................................................... 43

Contra-exemplul............................................................................................. 43

Surse de erori........................................................................................................ 43

Erori în discuţie............................................................................................ 43

Distincţia dispută/pledoarie.............................................................................. 43

Victoria în sub-dispută.................................................................................... 43

Identificarea subiectului................................................................................... 43

Distincţia dispută simplă/dispute asociate......................................................... 43

Identificarea concordanţelor şi a discordanţelor............................................... 43

Negarea definiţiei............................................................................................ 44

Sinonimia........................................................................................................ 44

Omonimia....................................................................................................... 44

Erori în argumentare................................................................................. 44

Transferul falsităţii prin implicaţie..................................................................... 44

Contra-contra-exemplul.................................................................................. 44

Strategii............................................................................................................ 44

Tehnici ne-ortodoxe................................................................................... 45

Exemple...................................................................................................................... 45

*** „Rămăşiţe” din versiuni mai vechi ale lucrării -----------------------------------------------

Types of Objection......................................................................................... 46

Definition........................................................................................................ 46

Un exemplu complex...................................................................................... 47

Structură ascunsă.................................................................................. 47

Structură multiplă – bază multiplă........................................................... 47

Înlănţuirea argumentelor......................................................................... 47

Implicaţia absolută şi implicaţia relativă............................................................ 49

Preambul

Această lucrare propune un model al disputei între parteneri umani. Scopul lucrării este să inventarieze mecanismele de funcţionare ale disputei şi să analizeze modul lor de lucru, oferind astfel o mai bună înţelegere asupra oricărei dispute – de la micile certuri cotidiene până la marile dispute politice. Această mai bună înţelegere poate furniza instrumente solide, atât pentru acela care construieşte o argumentaţie într‑o dispută, cât şi (mai ales!) pentru acela în pericol de a fi „păcălit” sau pus în dificultate de o argumentaţie vicleană.

Partea I – Discuţie

Cadrul general

Enunţuri şi atitudini. Definiţia discuţiei

Pentru a studia disputa, este nevoie mai întâi de studiul unui fenomen mai general: discuţia. Voi porni de la un exemplu ipotetic de discuţie între doi oameni, X şi Y (voi numi preopinenţi participanţii la o discuţie). Fie deci următoarea discuţie:

X: „Ionescu şi‑a cumpărat o maşină.”

Y: „Nu‑i adevărat, şi‑a cumpărat o garsonieră.”

X: „Eu am fost ieri cu el, când şi‑a cumpărat maşina.”

Y: „Ah, da?... Mie îmi spusese Cristina că Ionescu vroia să‑şi cumpere o garsonieră.”

Se observă că, în prima lui replică, Y spune de fapt două lucruri: afirmă întâi că enunţul lui X e fals, apoi face propria sa propunere de enunţ adevărat. Cele două afirmaţii au un rol diferit: împotrivirea la enunţul lui X este o părere, exprimă o convingere, şi nu influenţează relaţiile logice dintre enunţuri. Acestea din urmă sunt determinate exclusiv de raporturile logice dintre fapte, aşa cum sunt ele prezentate de preopinenţi. Se impune deci separarea acestor două aspecte, definind:

· planul enunţurilor (ce afirmă preopinenţii despre fapte) şi

· planul atitudinilor (cum îşi manifestă preopinenţii părerile despre adevărul enunţurilor).

O notă definitorie a oricărei discuţii este transferul de informaţie – preopinenţii (cel puţin unul din ei) caută să transmită (sau să afle) ceva. De aceea ei schimbă enunţuri privind fapte. Apariţia atitudinilor poate genera şi un motiv suplimentar de a purta o discuţie: modificarea atitudinilor preopinentului. Dar această componentă nu este definitorie pentru discuţie, ea putând să lipsească (după cum se va vedea, modificarea atitudinilor este importantă însă pentru dispută, pledoarie şi dezbatere).

Voi considera o discuţie ca fiind definită astfel:

O discuţie este un proces în care doi (sau mai mulţi) preopinenţi exprimă pe rând enunţuri despre nişte fapte, cu scopul de a schimba informaţii. Ei au nişte păreri despre adevărul acestor enunţuri, păreri pe care le fac uneori cunoscute prin atitudini.

Fapte şi enunţuri. Păreri şi atitudini

Făcând distincţia necesară dintre planul enunţurilor şi planul atitudinilor, primele două replici ale discuţiei dintre X şi Y s‑ar putea reprezenta astfel:

X: „Ionescu şi‑a cumpărat o maşină.”

Y (‚Enunţul lui X este fals.’): „Ionescu şi‑a cumpărat o garsonieră.”

Negaţia lui Y am reprezentat‑o ca pe o „indicaţie de regie” pentru a arăta că este vorba de o atitudine, adică un enunţ care nu afirmă ceva despre fapte, ci face cunoscută o părere despre adevărul altui enunţ. Atitudinile sunt deci mijloace de a exprima păreri despre adevărul enunţurilor. Există şi atitudini non‑verbale (ridicare din umeri, pufnit dezaprobator, aprobare prin mimică, prin mişcări ale capului etc.), toate mijloacele fiind la fel de „valabile” dacă îşi ating scopul.

Şi enunţurile propriu‑zise (privind faptele) pot fi uneori exprimate prin mijloace non‑verbale (indicarea unui obiect, de exemplu), dar aceasta nu le transformă în atitudini. Ceea ce contează este conţinutul informaţional: enunţurile aduc informaţii despre fapte, pe când atitudinile aduc informaţii despre păreri privind adevărul enunţurilor. În diagrama următoare se poate vedea cum faptele generează enunţuri, enunţurile generează păreri, care la rândul lor generează atitudini:

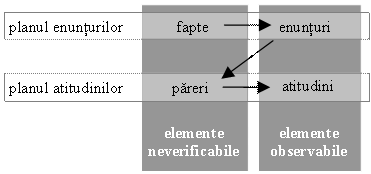
Faptele şi părerile sunt neverificabile, în sensul că un studiu al discuţiei nu poate (şi nu trebuie să încerce) să analizeze faptele – există discipline întregi al căror scop este tocmai determinarea cu maximă acurateţe a unor stări de fapt din diverse domenii – şi nici părerile – formarea părerilor poate fi studiată cu ajutorul psihologiei, detectorului de minciuni etc. Aşa cum, în justiţie, sarcina judecătorului nu este de a aduna probe (de acest lucru se ocupă Procuratura, Poliţia etc.), ci de a judeca pe baza probelor prezentate, tot astfel şi în studiul discuţiei, efortul trebuie concentrat înspre analiza relaţiilor reciproce dintre enunţuri şi atitudini, fără a pune problema adecvării enunţurilor la fapte şi a atitudinilor la păreri. Sarcina aceluia care studiază discuţia este să analizeze elementele direct accesibile observaţiei – enunţurile şi atitudinile –, lăsând în seama disciplinelor legitime studiul faptelor şi al părerilor.

Atitudine şi comportament

Fiecare dintre preopinenţi se raportează într‑un fel la orice enunţ aflat în discuţie, are o părere privind adevărul lui. Această părere se poate exterioriza printr‑o atitudine, dar nu e obligatoriu – atitudinea poate lipsi, părerea rămânând un „secret” al preopinentului. Aşa cum enunţurile sunt aproximări ale faptelor, şi atitudinile redau doar aproximativ părerile.

Aceste aproximări sunt singurele elemente accesibile observaţiei, studiului. Adecvarea enunţurilor la fapte nu face obiectul lucrării, iar părerile, convingerile intime sunt imposibil de determinat. De exemplu, un preopinent poate avea la un moment dat atitudinea „Bine, fie cum zici tu”, continuând apoi cu enunţul „În cazul ăsta rezultă că...” – el încearcă astfel să arate nişte consecinţe absurde ale enunţului celuilalt. Deşi probabil nu crede că enunţul ar fi adevărat, în mod formal el se comportă (o perioadă de timp) ca şi cum ar crede‑o. De fapt, nici nu este important care este convingerea reală, odată ce atitudinea descrie comportamentul în timpul discuţiei – adică exact ceea ce poate fi (şi trebuie) studiat.

Cu această observaţie, prin „părere” voi înţelege în continuare „acea convingere aparentă exprimată prin atitudine”, fără a mai preciza de fiecare dată că „reala convingere ar putea fi cu totul alta, dar nimeni nu poate verifica”.

Clasificarea atitudinilor

Notând atitudinea prin cuvântul care descrie părerea despre gradul de adevăr al enunţului, atitudinile propuse de acest model sunt:

fals: ‚Nu este adevărat că...’,

incert: ‚Nu ştiu, s‑ar putea... Nu pot nici să neg, nici să suţin că...’,

adevărat: ‚Este adevărat că...’

Trebuie remarcat că, deşi folosesc trei valori, nu este vorba de altceva decât de logica bivalentă clasică, pentru că rolul valorii „incert” este acela al unei variabile cu valoare necunoscută. Aşa cum introducerea notaţiei carteziene „x” în aritmetică nu a însemnat îmbogăţirea mulţimii numerelor cu un nou element, nici introducerea „incertului” nu scoate modelul folosit aici în afara logicii tradiţionale bivalente.

Axa atitudinilor. Spaţiul atitudinilor

Prin convenţie[1], voi reprezenta astfel cele trei atitudini pe axa atitudinilor:

Pentru doi preopinenţi, există 3²=9 combinaţii posibile de atitudini:

atitudinea lui X	atitudinea lui Y
fals	fals
fals	incert
fals	adevărat
incert	fals
incert	incert
incert	adevărat
adevărat	fals
adevărat	incert
adevărat	adevărat

Aceste nouă combinaţii pot fi reprezentate grafic în ceea ce voi numi spaţiul atitudinilor:

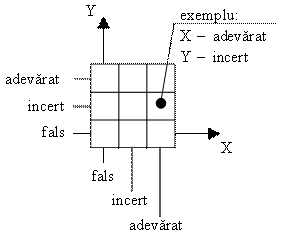
Fiecare căsuţă reprezintă o combinaţie, ea citindu‑se prin coordonatele căsuţei pe axa X, respectiv Y. Este important de înţeles că pe axa atitudinilor căsuţele reprezintă atitudini singulare, ale câte unui preopinent, pe când în spaţiul atitudinilor o căsuţă reprezintă o combinaţie de atitudini a doi preopinenţi. Pentru ca diagramele următoare să nu apară prea încărcate, în spaţiul atitudinilor voi renunţa să mai notez explicit valorile ‚fals’, ‚incert’ şi ‚adevărat’ pe cele două axe, contând pe faptul că cititorul a reţinut această ordine.

Convenţii privind atitudinile. Tranziţie

Un caz particular este acela când nu există nici o atitudine explicită. Părerea (ipotetică) asociată acestui caz fiind indeterminată, o voi considera ‚incert’ – ca şi cum preopinentul ar spune „Hmm... Nu pot nici să neg hotărât, nici să fiu de acord fără rezerve...”

Un alt caz particular este acela când un preopinent enunţă ceva – evident, el crede ceea ce spune (sau cel puţin se comportă ca şi cum ar crede), adică are părerea ‚adevărat’ despre propria afirmaţie (măcar în momentul enunţării). De aceea, chiar dacă atitudinea explicită lipseşte, voi asocia fiecărei enunţări atitudinea ‚adevărat’ din partea autorului ei. Această convenţie se aplică numai în momentul enunţării, pentru că, ulterior, preopinentul îşi poate schimba atitudinea faţă de propriul enunţ.

Voi spune că are loc o tranziţie în raport cu un enunţ dacă un preopinent îşi schimbă atitudinea faţă de el (mai simplu spus, tranziţia înseamnă schimbarea părerii[2]).

Posibilitatea tranziţiei conduce la o altă convenţie: odată ce este cunoscută o atitudine a unui preopinent faţă de un enunţ, voi considera că această atitudine a sa este valabilă până la prima tranziţie a preopinentului în raport cu respectivul enunţ.

Spaţiul enunţurilor. Spaţiul enunţurilor acceptate

Definesc spaţiul enunţurilor ca fiind totalitatea enunţurilor aflate în discuţie la un moment dat. Pentru un preopinent, definesc spaţiul enunţurilor acceptate astfel:

Pentru fiecare enunţ aflat în discuţie,

· dacă atitudinea preopinentului este ‚adevărat’, atunci îl reţin ca atare;

· dacă atitudinea preopinentului este ‚fals’, atunci reţin negaţia enunţului;

· dacă atitudinea preopinentului este ‚incert’, atunci nu reţin nici enunţul, nici negaţia.

Evident, spaţiul enunţurilor este dinamic şi creşte în timp o dată cu adăugarea de noi enunţuri. La fel este şi spaţiul enunţurilor acceptate de un preopinent (deşi acesta poate creşte mai lent, deoarece enunţurile faţă de care atitudinea este ‚incert’ nu îl îmbogăţesc).

Tabelul de stare

Reluând exemplul discuţiei dintre X şi Y, se poate construi tabelul de stare al discuţiei, care arată ce enunţă fiecare preopinent, precum şi ce atitudine are fiecare vizavi de enunţuri. La momentul iniţial, tabelul de stare conţine o singură linie:

cine	ce enunţă	atitudinea lui X	atitudinea lui Y
X	„Ionescu şi‑a cumpărat o maşină.”	adevărat	incert

                                                       prin convenţie, pentru că                               ô

                                                        X tocmai a enunţat ceva                               ô

                                                                                        prin convenţie, pentru că

                                                                  Y n-a apucat să-şi exprime vreo părere

După ce Y îşi exprimă părerea (‚fals’) şi expune viziunea lui asupra faptelor, tabelul devine (am marcat cu gri schimbările – adăugirile sau modificările):

cine	ce enunţă	atitudinea lui X	atitudinea lui Y
X	„Ionescu şi‑a cumpărat o maşină.”	adevărat	fals
Y	„Ionescu şi‑a cumpărat o garsonieră.”	incert	adevărat

                                                       prin convenţie, pentru că                               ô

                             X n-a apucat încă să afişeze vreo atitudine                               ô

                                                                                        prin convenţie, pentru că

                                                                                         Y tocmai a enunţat ceva

X continuă să nu afişeze vreo atitudine (rămâne în ‚incert’) faţă de acest enunţ, dar adaugă un nou enunţ:

cine	ce enunţă	atitudinea lui X	atitudinea lui Y
X	„Ionescu şi‑a cumpărat o maşină.”	adevărat	fals
Y	„Ionescu şi‑a cumpărat o garsonieră.”	incert	adevărat
X	„Am fost cu Ionescu când şi‑a cumpărat maşina.”	adevărat	incert

Y se pare că îl crede pe X, fapt ce duce şi la o tranziţie a sa faţă de enunţul pe care iniţial îl nega:

cine	ce enunţă	atitudinea lui X	atitudinea lui Y
X	„Ionescu şi‑a cumpărat o maşină.”	adevărat	incert
Y	„Ionescu şi‑a cumpărat o garsonieră.”	incert	adevărat
X	„Am fost cu Ionescu când şi‑a cumpărat maşina.”	adevărat	adevărat

                                               Y acceptă argumentul lui X (el spune „Ah, da?...”),

                            ceea ce înseamnă că şi-a schimbat atitudinea faţă de primul enunţ

                                  (dacă la început îl considera ‚fals’, acum îl consideră ‚incert’)

După aceasta, Y mai adaugă o linie:

cine	ce enunţă	atitudinea lui X	atitudinea lui Y
X	„Ionescu şi‑a cumpărat o maşină.”	adevărat	incert
Y	„Ionescu şi‑a cumpărat o garsonieră.”	incert	adevărat
X	„Am fost cu Ionescu când şi‑a cumpărat maşina.”	adevărat	adevărat
Y	„Mi‑a spus Cristina că Ionescu vroia să‑şi cumpere o garsonieră.”	incert	adevărat

Tabelul de stare „fotografiază” spaţiul enunţurilor (în primele două coloane) şi spaţiile atitudinilor faţă de enunţuri[3] (în următoarele coloane) – împreună, acestea definesc starea unei discuţii la un moment dat. Tabelul de stare este o structură dinamică, care se modifică în timp – valoarea lui ca instrument de studiu constă tocmai în această reflectare sintetică a schimbărilor de la un moment la altul. Păstrând analogia cu fotografia, „filmul” stărilor oferă o mult mai bună înţelegere decât orice „stop‑cadru” izolat, fie el în momentul iniţial, final, sau în orice alt moment.

Dispută

Apariţia disputei. Subiectul disputei

Exemplul de discuţie studiat până acum este evident o dispută. Caracteristica esenţială ce se poate observa este împotrivirea unui preopinent la enunţul celuilalt – altfel, totul ar rămâne la nivelul unui schimb de replici neutre. Pentru ca disputa să apară, este deci suficient (şi necesar) ca unul dintre preopinenţi să aibă atitudinea ‚fals’ faţă de un enunţ pe care celălalt îl crede ‚adevărat’. Aceasta conduce la următoarea definiţie:

Într‑o discuţie, se spune că apare o dispută atunci când există un enunţ E pe care un preopinent îl consideră ‚adevărat’, iar celălalt ‚fals’. Subiectul disputei este acel enunţ. Notez subiectul disputei cu ?E[4].

Dacă se reprezintă cei doi preopinenţi pe axa atitudinilor, se observă că, iniţial, ei au poziţii simetrice faţă de centru:

În spaţiul atitudinilor, pentru doi preopinenţi există două situaţii posibile, care se evidenţiază prin ceea ce voi numi puncte‑dispută (notate cu simbolul ?):

Evident, subiectul unei dispute este unic. Totuşi, ce se întâmplă dacă, într‑o dispută deja amorsată, unul din preopinenţi neagă un enunţ apărut pe parcurs? Acel enunţ va genera o nouă dispută, care va „pune în aşteptare” disputa iniţială – odată această sub‑dispută încheiată, rezultatul ei va putea fi folosit pentru continuarea disputei iniţiale. Deşi acesta este mecanismul cel mai frecvent, disputa iniţială nu este totuşi „blocată” cât timp sub‑disputa nu s‑a soluţionat. Odată ce nu există vreo restricţie formală privind momentul (şi motivul) tranziţiilor, disputa iniţială s‑ar putea soluţiona brusc, „de la sine”, în timp ce sub‑disputa continuă („Stai puţin... Uite, acum îmi dau seama că aveai dreptate în ce spuneai când am început să ne certăm. Dar, oricum, chestia pe care ai zis‑o adineaori continuă să mi se pară inacceptabilă.”). Se poate întâmpla şi invers, sub-disputa să se soluţioneze, dar disputa iniţială să continue. Din păcate, de multe ori victoria în sub-dispută este greşit înţeleasă ca victorie în disputa iniţială.

Soluţie a disputei

Este logic să se presupună că disputa încetează atunci când preopinenţii nu mai au atitudini opuse faţă de subiectul disputei. Definesc deci soluţionarea disputei astfel:

O dispută este soluţionată atunci când atitudinile preopinenţilor faţă de subiect nu mai sunt ‚adevărat’ şi ‚fals’, ci orice altă combinaţie.

Este important de observat că această definiţie nu cere ca preopinenţii să fie neapărat de acord unul cu celălalt. Într‑adevăr, reluând exemplul de la început, disputa se soluţionează cu Y având atitudinea finală de incertitudine, care nu înseamnă că‑i dă dreptate lui X, ci doar că renunţă să‑l mai contrazică.

În total, pentru doi preopinenţi, teoretic sunt 7 cazuri posibile de soluţionare (din cele 9 combinări, două nu soluţionează disputa – ‚fals’‑‘adevărat’ şi ‚adevărat’‑‘fals’):

		atitudinea lui X	atitudinea lui Y
	iniţial	adevărat	fals
		fals	fals	soluţie, tranziţie X
		fals	incert	dublă tranziţie
		fals	adevărat	nu este soluţie
		incert	fals	soluţie, tranziţie X
	în final	incert	incert	dublă tranziţie
		incert	adevărat	dublă tranziţie
		adevărat	fals	nu este soluţie
exemplul studiat ®		adevărat	incert	soluţie, tranziţie Y
		adevărat	adevărat	soluţie, tranziţie Y

Din tabel se observă că soluţii cu o singură tranziţie sunt patru (două cu tranziţie X, două cu tranziţie Y). Celelalte, cu două tranziţii, sunt soluţii imposibil de atins practic, deoarece preopinenţii nu pot avea tranziţii perfect simultan – unul din ei va avea tranziţie obligatoriu primul, moment în care disputa se termină. Starea în care se ajunge după ce are loc şi tranziţia celuilalt nu este soluţie a disputei din simplul motiv că în acel moment nu mai există nici o dispută.

În spaţiul atitudinilor, condiţia unei unice tranziţii se traduce prin restricţia ca deplasarea din punctul‑dispută să se facă numai pe verticală sau orizontală (pe orice distanţă – o căsuţă sau două), niciodată pe diagonală:

Pentru celălalt punct‑dispută, diagrama este simetrică (faţă de prima bisectoare).

Cu aceste precizări, se poate da acum o definiţie mai practică a soluţionării disputei:

O dispută se soluţionează atunci când apare o tranziţie a unuia din preopinenţi în raport cu subiectul (adică preopinentul îşi schimbă atitudinea faţă de subiect).

Victorie

În urma soluţionării unei dispute, voi numi învingător preopinentul care nu efectuează tranziţie. În continuare definesc două tipuri de victorie:

- victorie absolută este aceea în care adversarul a fost adus la părerea învingătorului

- victorie relativă este acea în care adversarul a încetat să‑l mai contrazică pe învingător, retrăgându‑se în incertitudine.

Se observă că aceste definiţii acoperă tot spectrul de soluţii posibile ale unei dispute:

Dispute asociate. Pivot

Este important de observat că, în exemplul studiat, subiectul disputei este ?„Ionescu şi‑a cumpărat o maşină”, enunţul „Ionescu şi‑a cumpărat o garsonieră” neavând nici un rol în dispută (Y ar fi putut numai să nege afirmaţia lui X, fără să propună vreo altă variantă, şi esenţa disputei ar fi fost aceeaşi, anume „şi-a cumpărat sau nu Ionescu o maşină?”). Faptul că totuşi Y propune propria variantă nu are nici o relevanţă în dispută atâta timp cât X nu se împotriveşte. Ce s‑ar fi întâmplat, totuşi, dacă X s‑ar fi împotrivit şi el versiunii propuse de Y? Ar fi fost vorba atunci de două dispute, una cu subiectul ?„Ionescu şi‑a cumpărat o maşină”, iar cealaltă cu subiectul ?„Ionescu şi‑a cumpărat o garsonieră”. Este important de observat că acestea sunt două variante care nu se exclud reciproc (Ionescu putea să‑şi cumpere şi o garsonieră şi o maşină, sau să nu‑şi cumpere nici una, nici alta). Cele două dispute pot evolua simultan, „împletite”, dar a considera că este vorba de o singură dispută ar fi o greşeală. Totuşi, cele două subiecte având destul de multe în comun, se impune definirea asocierii unor dispute:

Două dispute se numesc asociate dacă subiectele lor sunt particularizări ale unui enunţ mai general. Acest enunţ general este pivotul disputelor asociate.

Concordanţe, discordanţe şi versiuni

Elementele comune ale pivotului, acceptate de toţi preopinenţii, le numesc concordanţe. Elementul variabil, cel pentru care fiecare preopinent propune altceva, îl numesc discordanţă şi îl marchez cu prefixul interogaţiei, „?”. Propunerile concrete ale preopinenţilor privind rezolvarea discordanţei le numesc versiuni ale preopinenţilor.

În exemplul studiat, pivotul ar fi „Ionescu şi‑a cumpărat o ?ceva”, concordanţele sunt „Ionescu”, „a cumpărat”, „pentru sine” şi „o singură”, discordanţa este „?ceva”, iar versiunile preopinenţilor sunt „maşină” şi „garsonieră”. Este corect a numi acest enunţ general „pivot al unor dispute asociate” numai dacă fiecare preopinent se împotriveşte variantei propuse de celălalt – altfel nu există simetrie, preopinenţii nu „pivotează” prin dispute asociate în jurul acestui enunţ, ci în jurul subiectului unicei dispute ?„Ionescu şi‑a cumpărat o maşină”.

În termeni de calcul al predicatelor, pivotul este un predicat propoziţional de mai multe variabile, P(x, a, b, g...), unde a, b, g... sunt concordanţe (constante), iar x este discordanţa (variabilă liberă, pentru care cei doi preopinenţi propun soluţiile x₁ şi x₂ – acestea fiind versiunile lor). Deoarece a, b, g... sunt constante, pivotul se mai poate scrie P(x). Subiectele celor două dispute asociate sunt ?P(x₁) şi ?P(x₂): un preopinent susţine „P(x₁) şi ¬P(x₂)”, iar celălalt „¬P(x₁) şi P(x₂)”:

	primul preopinent		al doilea preopinent
P(x1)	adevărat	¬ disputa ?P(x1)  ®	fals
P(x2)	fals	¬  disputa ?P(x2)  ®	adevărat

Este important de remarcat că enunţurile compuse „P(x₁) şi ¬P(x₂)”, respectiv „¬P(x₁) şi P(x₂)” nu sunt unul negaţia celuilalt, deci poziţiile preopinenţilor nu sunt logic opuse. Acest lucru explică faptul că nu întotdeauna ambele dispute sunt câştigate de acelaşi preopinent: se poate întâmpla, de exemplu, ca P(x₁) şi P(x₂) să fie ambele adevărate – caz în care disputa ?P(x₁) este câştigată de primul preopinent, iar disputa ?P(x₂) de al doilea.

Reducerea unei asocieri de dispute la o dispută simplă

Posibilitatea ca P(x₁) şi P(x₂) să fie simultan adevărate (sau simultan false) arată că, în general, aceste enunţuri nu sunt unul negaţia celuilalt. (Exemplu: „Ionescu este profesor” şi „Ionescu este înalt” nu sunt în relaţie logică de opoziţie.)

Cazul particular în care P(x₁) este în relaţie logică de opoziţie cu P(x₂) conduce la o dispută simplă, cu subiectul ?P(x₁) (sau, echivalent, ?¬P(x₂)). Rezultă că pentru a putea reduce o asociere de două dispute la o dispută simplă, trebuie ca versiunile celor doi preopinenţi să fie logic opuse.

Este foarte importantă verificarea acestei condiţii înainte de a decide dacă este vorba despre două dispute asociate sau despre o dispută simplă. Situaţiile cele mai clare sunt acelea în care versiunile celor doi preopinenţi sunt opuse prin definiţie. (Exemplu: „Ionescu este înalt” şi „Ionescu este scund” conduc la o dispută simplă, pentru că „scund” este, prin definiţie, opusul lui „înalt”). Situaţia când cele două versiuni nu sunt opuse prin definiţie trebuie tratată cu atenţie, pentru că ele ar putea numai să pară că se exclud reciproc, nefiind totuşi absurd să fie simultan adevărate (sau simultan false). (Exemplu: „Particula este corpuscul” versus „Particula este undă” nu conduce la o dispută simplă, pentru că unda nu este opusul, contrarul corpusculului; noţiunile nu sunt opuse nici prin definiţie şi nici altfel – ele pur şi simplu se pot manifesta simultan sau pot lipsi simultan.)

De fapt, regula se poate aplica şi în sens invers: Dacă o asociere de două dispute se reduce la o dispută simplă, atunci înseamnă că există motive temeinice ca versiunile să fie logic opuse.

Pledoarie

Definiţie

Disputa apare atunci când faţă de un enunţ există atitudini extreme: una ‚fals’, alta ‚adevărat’. Dacă numai una dintre atitudini este extremă (‚adevărat’ sau ‚fals’), iar cealaltă este ‚incert’, în practică se observă că, deşi ceea ce apare nu respectă condiţia de apariţie a unei dispute, totuşi preopinenţii se pot „aprinde” destul de tare în discuţie. Reluând exemplul iniţial, o astfel de situaţie ar putea să apară dacă discuţia ar începe cu:

X: „Ionescu şi‑a cumpărat o maşină.”

Y: „Hmm... Nu prea‑mi vine a crede...”

Ca urmare a reacţiei ‚incert’ a lui Y, X ar putea să‑ncerce să‑l convingă de adevărul spuselor sale, adică să‑i schimbe atitudinea în ‚adevărat’. Numesc aceasta o pledoarie:

Într‑o discuţie, se spune că apare o pledoarie atunci când există un enunţ E faţă de care unul din preopinenţi are atitudinea ‚incert’, iar celălalt o atitudine diferită de ‚incert’ (fie ‚adevărat’, fie ‚fals’). Subiectul pledoariei este acel enunţ. Notez subiectul pledoariei cu >E.

În spaţiul atitudinilor sunt patru puncte‑pledoarie (le voi nota prin semnul >):

Pentru a recunoaşte pledoaria, este foarte importantă distincţia între ‚Nu cred că...’ şi ‚Cred că nu...’ – prima formulare înseamnă ‚Nu sunt absolut convins, nu pot să jur că aşa e. Ar putea să fie, ar putea să nu fie... Convinge‑mă’, pe când cea de‑a doua înseamnă ‚Sunt absolut convins, susţin cu tărie că nu este aşa.’ Prima atitudine conduce la pledoarie, pe când cea de‑a doua generează dispută.

Asimetrie. Avocat şi spectator

Se observă că, spre deosebire de dispută, într‑o pledoarie rolul preopinenţilor nu mai este simetric: unul încearcă să‑l aducă pe celălalt dintr‑o poziţie neutră, de mijloc, către extremitatea în care se situează el (‚adevărat’ sau ‚fals’), pe când „necredinciosul” încearcă (eventual) să se opună acestei deplasări. Se poate întâmpla şi invers, „necredinciosul” să încerce să‑l convingă pe cel sigur pe el că ar fi cazul să‑şi pună nişte întrebări, să se îndoiască, să nu mai fie atât de sigur. Importante în această asimetrie nu sunt „tendinţele de mişcare”, pentru că acestea ascund de fapt motivaţii, care, nefiind observabile în mod obiectiv, nu pot avea nici un rol în model. Importantă este asimetria poziţiilor iniţiale pe axa atitudinilor:

 sau

Această asimetrie impune o diferenţiere de notaţie în privinţa preopinenţilor – pe cel neutru, care la început se îndoieşte, îl voi numi spectator, iar pe cel sigur de el îl voi numi avocat. În funcţie de poziţia sa pe axa atitudinilor, avocatul poate fi avocat contra (dacă susţine ‚fals’) sau avocat pro (dacă susţine ‚adevărat’).

Soluţie a pledoariei

Ca şi disputa, pledoaria încetează atunci când apare o tranziţie a unuia din preopinenţi în raport cu subiectul. Construind un tabel similar cu cel pentru soluţionarea disputei, se observă că asimetria pledoariei conduce la o asimetrie a soluţiilor posibile:

	atitudinea lui X (avocat)	atitudinea lui Y (spectator)
iniţial	adevărat	incert
	fals	fals	dublă tranziţie
	fals	incert	nu este soluţie (!)
	fals	adevărat	dublă tranziţie
	incert	fals	dublă tranziţie
în final	incert	incert	soluţie, tranziţie X
	incert	adevărat	dublă tranziţie
	adevărat	fals	soluţie, tranziţie Y
	adevărat	incert	nu este soluţie
	adevărat	adevărat	soluţie, tranziţie Y

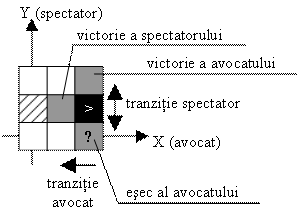
Există două soluţii în care spectatorul efectuează tranziţie (într‑un caz este convins de avocat, în celălalt caz pledoaria are un efect contrar, ei ajungând la dispută), dar apare o singură soluţie cu tranziţia avocatului – atunci când el ajunge să‑i dea dreptate spectatorului în îndoiala lui. Cazul când avocatul trece în extrema cealaltă, negându‑şi propriul enunţ iniţial, nu este soluţie pentru că se ajunge la o nouă pledoarie, cu aceiaşi actori dar cu subiect contrar. Aceste situaţii se observă şi în spaţiul atitudinilor:

Victorie

Ca şi la dispută, preopinentul care‑şi schimbă părerea nu poate fi victorios. Dar cel care nu-şi schimbă părerea nu devine automat victorios, pentru că soluţia‑dispută evidenţiată mai sus este un caz care cu greu ar putea fi numit „victorie a avocatului” (deşi el rămâne neclintit în convingerile sale). Această soluţie particulară o voi numi eşec al avocatului[5]. Celelalte două soluţii, nemaibeneficiind de simetria disputei, le voi numi simplu:

- victorie a avocatului

- victorie a spectatorului.

Pledoarii asociate. Asocierea pledoarie‑dispută

Ca şi pentru dispută, două pledoarii pot fi asociate dacă au ca subiecte particularizări ale unui enunţ mai general (pivotul pledoariilor). De exemplu:

X: „Ionescu şi‑a cumpărat o maşină.”

Y: „Hmm... nu prea‑mi vine a crede că şi‑a luat maşină. Eu ştiu sigur de‑o garsonieră...”

X: „Garsonieră? Posibil şi asta, deşi mi se pare dubios... Maşina şi‑a luat‑o ieri, am fost eu cu el.”

În acest caz, niciunul din ei nu crede în totalitate ce spune celălalt (fără să nege însă!), deci probabil vor încerca să se convingă reciproc (de fapt, X începe deja, aducând argumentul „Am fost eu cu el”).

Definirea pledoariei poate lămuri acum situaţia exemplului de la începutul lucrării, când Y se împotrivea afirmaţiei lui X, propunând în acelaşi timp o variantă faţă de care X era indiferent, neutru: „Ionescu şi‑a cumpărat o maşină” era clar subiectul unei dispute, pe când „Ionescu şi‑a cumpărat o garsonieră” era subiectul pledoariei prin care Y încerca să‑l convingă pe X de justeţea versiunii sale. Dealtfel, Y persistă în pledoarie chiar şi după încheierea disputei – el susţine „Mi‑a spus Cristina că Ionescu vroia să‑şi cumpere o garsonieră” tocmai pentru că nu renunţă la a‑l convinge pe X. Enunţul mai general şi cele două particularizări ale sale există şi aici, ceea ce conduce la definirea asocierii dintre o dispută şi o pledoarie în mod similar asocierii a două dispute:

	primul preopinent		al doilea preopinent
P(x1)	adevărat	¬ disputa ?P(x1)   ®	fals
P(x2)	incert	¬ pledoaria >P(x2) ®	adevărat

Consens

Cazurile studiate până acum (pentru doi preopinenţi) sunt:

‑ două atitudini extreme (disputa)

‑ o atitudine „de mijloc” şi cealaltă extremă (pledoaria).

Se observă uşor că singurul caz neluat în considerare până acum este:

‑ două atitudini identice (fie ele la o extremă, la cealaltă sau la mijloc).

Voi numi această situaţie consens:

Într‑o discuţie, spun că are loc un consens dacă atitudinile preopinenţilor faţă de un enunţ E sunt identice. Acel enunţ este subiectul consensului. Notez subiectul consensului cu !E.

În spaţiul atitudinilor există trei puncte‑consens (pe care le voi nota cu !):

Dacă situaţiile extreme sunt frecvent întâlnite în practică, consensul „de mijloc” ar putea însă să pară puţin mai ciudat. Un exemplu ar fi situaţia când doi anchetatori pornesc o dispută pe tema „Este Ionescu criminalul?” (evident, unul din ei susţine că da, celălalt că nu), ambii ajungând în final la concluzia comună că „Nu se ştie. Ar putea să fie, ar putea să nu fie...” Ceea ce contează în acest exemplu nu este situaţia iniţială şi nici măcar evoluţia discuţiei, ci starea finală de incertitudine comună a celor doi preopinenţi.

Consensul încetează atunci când atitudinile preopinenţilor nu mai sunt identice. Nu numesc aceasta „soluţie” a consensului pentru că, spre deosebire de dispută şi pledoarie (care ar putea fi concepute ca nişte „probleme” şi deci acceptă, ba chiar au nevoie de soluţii), consensul nu este ceva nedorit, din care preopinenţii caută să iasă, ci este de obicei o stare stabilă, de echilibru (care nu cere să fie soluţionată, ci este ea însăşi o soluţie).

Tot din motive practice nu este de mare ajutor nici definirea asocierii a două consensuri (deşi definiţia este perfect posibilă, similar cu asocierea disputelor şi a pledoariilor). La fel, un consens se poate asocia cu o dispută sau o pledoarie, dar asocierile respective nu sunt interesante practic.

Dinamica discuţiei

Numai trei posibilităţi: dispută, pledoarie sau consens

Disputa (2 cazuri), pledoaria (4 cazuri) şi consensul (3 cazuri) epuizează cele 9 puncte din spaţiul atitudinilor:

Oricare din aceste puncte reprezintă o combinaţie posibilă de atitudini a doi preopinenţi faţă de un enunţ. Faptul că nu există combinaţii neacoperite de situaţiile studiate până acum înseamnă că, dat fiind un enunţ, doi preopinenţi trebuie să aibă ori o dispută, ori o pledoarie, ori un consens vizavi de el.

Afirmaţia că, într‑o discuţie, orice enunţ asupra căruia preopinenţii nu sunt perfect de acord conduce ori la dispută ori la pledoarie ar putea să pară ciudată. Sensul ei (ca şi a modelului schiţat până aici, dealtfel) este pur descriptiv şi nu se referă la angajarea efectivă a preopinenţilor, cu consum de timp şi energie, în disputele şi pledoariile generate de fiecare enunţ. Formal, o pledoarie este şi aceasta:

– Mi‑am cumpărat o cămaşă de cinci sute de mii de lei.

– Bine... Hai că te las, trebuie să prind autobuzul.

Nu contează că discuţia nu continuă, că nimeni nu încearcă să convingă pe nimeni. Pledoaria apare, dar nu se dezvoltă, nu se soluţionează. Motivele care o fac să rămână în acest stadiu incipient (sau care ar putea‑o face să se dezvolte furtunos) sunt exterioare modelului, a cărui unică sarcină este să recunoască un tip de relaţie între preopinenţi, indiferent de atenţia pe care ei o acordă respectivei relaţii.

Tranziţii în spaţiul atitudinilor

Dat fiind un enunţ şi raportarea a doi preopinenţi la el (dispută, pledoarie, consens), ei pot trece dintr‑una în alta prin tranziţie. De exemplu, o dispută poate trece în pledoarie sau consens:

Un caz de importanţă practică deosebită este acela când disputa se transformă în pledoarie (victorie relativă). Deoarece energia consumată de avocat în pledoarie este comparabilă cu cea pe care‑o consumase în disputa premergătoare, el ar putea avea impresia că disputa nu s‑a încheiat (în momentul când celălalt a încetat să‑l mai contrazică, retrăgându‑se în incertitudine, în scepticism) şi că ea continuă la fel ca înainte. De aceea, nesoluţionarea unei pledoarii născute dintr-o dispută este uneori greşit înţeleasă ca nesoluţionare a disputei iniţiale, care de fapt se încheiase între timp. Faptul că pledoaria „se naşte” din dispută nu înseamnă că disputa „continuă să trăiască” prin pledoarie – disputa s‑a încheiat, s‑a soluţionat, a încetat să mai existe, altfel pledoaria n‑ar fi apărut.

Şi pledoaria se poate transforma prin tranziţie în consens sau dispută. Evident, şi din consens se poate trece în oricare din celelalte două categorii. Diagramele posibile sunt prea evidente şi prea numeroase pentru a le mai prezenta aici, dar cititorul curios le poate uşor alcătui, ca exerciţiu. În ceea ce priveşte soluţiile disputei şi ale pledoariei, observaţiile se pot sintetiza astfel:

pentru o dispută:

          victorie absolută ® consens (2 cazuri: învinge X sau învinge Y)

          victorie relativă ® pledoarie (2 cazuri: învinge X sau învinge Y)

pentru o pledoarie:

          victorie ® consens (2 cazuri: învinge avocatul sau învinge spectatorul)

          eşec ® dispută (1 caz: eşecul avocatului)

Concluzia este că discuţia evoluează prin tranziţii în spaţiul atitudinilor. Trebuie subliniat că fiecare enunţ are propria sa diagramă în spaţiul atitudinilor, incompatibilă, incomparabilă cu şi independentă de celalte. Aşa cum arătam şi la tabelul de stare (ale cărui ultime coloane se pot înlocui, dealtfel, cu o coloană de diagrame în spaţiul atitudinilor – câte una pentru fiecare enunţ), studiul trebuie centrat pe modificări, pe schimbări de atitudine, adică pe tranziţii.

Totuşi, a patra posibilitate: dezbatere

Încă un preopinent. Definiţia dezbaterii

Efectul apariţiei unui al treilea preopinent în spaţiul atitudinilor poate fi de întărire a poziţiei unuia din primii doi (dacă atitudinea lui coincide cu a respectivului), dar acest caz este neinteresant, pentru că poziţiile rămân aceleaşi cu cele studiate până acum, deci toate consideraţiile de până acum sunt valabile şi nu apare nimic nou. Pe axa atitudinilor se vede cel mai clar că singura situaţie fundamental nouă este aceea când cei trei preopinenţi ocupă toate poziţiile posibile (al treilea vine să „completeze” un loc liber lăsat de ceilalţi doi):

Nu are importanţă care puncte îi reprezintă pe primii doi şi care pe al treilea, odată ce distribuţia finală este perfect simetrică. Fenomenul asociat acestei distribuţii îl voi numi dezbatere:

Într‑o discuţie la care participă trei preopinenţi, se spune că apare o dezbatere atunci când cei trei au atitudinile ‚fals’, ‚incert’ şi ‚adevărat’ faţă de un enunţ E. Acel enunţ este subiectul dezbaterii. Notez subiectul unei dezbateri cu DE.

Deşi dezbaterea este perfect simetrică pe axa atitudinilor, prin analogie cu pledoaria voi da totuşi denumiri distincte celor trei: spectatorul este cel cu atitudinea ‚incert’, avocatul pro este cel cu ‚adevărat’, iar avocatul contra cel cu ‚fals’. La fel ca la pledoarie, aceste denumiri servesc numai la mai uşoara identificare a preopinenţilor şi nu reflectă neapărat gradul lor de angajare în discuţie.

Componentele dezbaterii

De fapt nu este vorba doar de o analogie cu pledoaria, ci de apariţia efectivă a unor pledoarii, care justifică astfel perfect convenţiile de notaţie de mai sus. Existenţa acestor componente decurge din chiar definiţia dezbaterii, dacă se analizează relaţiile dintre cei trei preopinenţi luaţi doi câte doi:

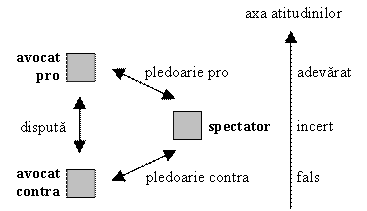
Din această diagramă „în triunghi” se vede că dezbaterea este un fenomen complex de interacţiune a unei dispute cu două pledoarii (un fel de „dispută cu spectator”), care însă nu poate fi redus la nici una dintre componente.

Un exemplu foarte bun de dezbatere este o dispută electorală televizată: cei doi candidaţi nu au de fapt ca scop convingerea adversarului, ci a electorului‑telespectator, ei desfăşurând în consecinţă nişte pledoarii îndreptate spre terţul preopinent (spectatorul). Totuşi, disputa dintre candidaţi nu este doar un pretext pentru două pledoarii, ea joacă un rol activ în dezbatere, pentru că a‑l face pe celălalt să nu mai susţină contrariul a ceea ce susţin eu este un ajutor preţios în pledoaria mea faţă de spectator şi m‑ar putea face să‑l aduc mai uşor la poziţia mea. Oricum, după ce X câştigă în disputa cu Y, discuţia nu mai este o dezbatere, pentru că nu mai există avocat contra. Dacă Y s‑a retras în incertitudine, atunci poziţia lui este identică cu a spectatorului, iar dacă a ajuns chiar să‑i dea dreptate lui X, atunci ambii sunt aliaţi în pledoaria pro (singura care mai există).

Ca şi în exemplele precedente, trebuie observat că motivaţiile, intenţiile preopinenţilor nu joacă nici un rol în model (le‑am adus în discuţie numai pentru a face exemplele mai inteligibile, mai grăitoare şi mai credibile).

Spaţiul tridimensional al atitudinilor

Pentru trei preopinenţi, spaţiul atitudinilor trebuie să conţină trei axe ale atitudinilor (X, Y şi Z), şi nu două, ca până acum. Aşa cum am văzut, trei preopinenţi pot avea o dispută, o pledoarie, un consens sau o dezbatere. Notând, ca şi până acum, punctele‑dispută cu ?, punctele‑pledoarie cu > şi punctele‑consens cu !, şi introducând pentru punctele‑dezbatere notaţia D, poziţiile acetor puncte în spaţiul tridimensional al atitudinilor sunt:

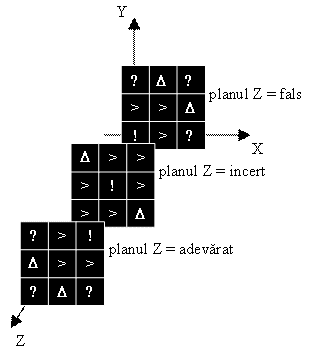
Se observă că din cele 3 ´ 3 ´ 3 = 27 de puncte, 6 reprezintă dispute, 12 pledoarii, 3 consensuri şi 6 dezbateri.

Tranziţiile în spaţiul tridimensional al atitudinilor se pot face după axa X sau Y (ca şi în spaţiul bidimensional), dar şi după axa Z.

Soluţionarea dezbaterii

Ca şi disputa, pledoaria sau consensul, dezbaterea încetează când unul din preopinenţi efectuează o tranziţie în spaţiul atitudinilor. Este interesant de observat că, în acest mod, dezbaterea poate trece în dispută sau pledoarie, dar nu şi în consens (din situaţia de „răspândire” iniţială pe axa atitudinilor, o singură tranziţie nu‑i poate strânge pe toţi trei preopinenţii într‑un unic punct).

Asocierea dezbaterii. Importanţa asocierii în general

La fel ca şi disputa sau pledoaria, o dezbatere poate avea ca subiect o particularizare a unui enunţ mai general, în timp ce o altă variantă de particularizare adusă în discuţie dă naştere unui fenomen asociat dezbaterii (fie el dispută, pledoarie sau tot dezbatere), care evoluează în paralel. Enunţul general este pivotul asocierii.

Iată un exemplu, bazat pe pivotul „E albă/neagră”:

Diagrame asemănătoare se pot construi şi pentru alte asocieri. Asocierile nu sunt importante pentru că ar da naştere în mod obiectiv vreunui fenomen deosebit de interdependenţă, ci pentru că, în practică, ele sunt deseori confundate cu fenomene simple. În exemplul de mai sus, un observator (sau spectator) neatent ar putea crede că „E albă” şi „E neagră” se exclud reciproc, considerând că „E neagră” şi „Nu e albă” înseamnă unul şi acelaşi lucru şi privind totul ca pe o dezbatere simplă. Eroarea din această presupunere devine evidentă dacă ne închipuim că obiectul în discuţie este o tablă de şah, cu pătrăţele albe şi negre. Sau un obiect roşu.

A cincea posibilitate nu există

Introducerea celui de‑al treilea preopinent a dus la definirea dezbaterii, care s‑a adăugat astfel disputei, pledoariei şi consensului. Cu aceasta, numărul relaţiilor posibile a ajuns la patru. Un rezultat deosebit de valoros al modelului pe care‑l propun este următorul:

Despre oricâţi preopinenţi ar fi vorba, faţă de un enunţ ei pot avea numai o dispută, o pledoarie, un consens sau o dezbatere. O a cincea posibilitate nu există.

Demonstraţia riguroasă, prin inducţie matematică, este prezentată în Anexă. O justificare poate fi însă schiţată aici. Fie un grup de preopinenţi care au nişte atitudini faţă de un enunţ. Un preopinent suplimentar, „nou venit”, poate întâlni trei situaţii posibile:

1. primii preopinenţi ocupă toţi un acelaşi loc în paleta fals‑incert‑adevărat (au un consens); „noul venit” se poate ralia părerii grupului (caz în care se ajunge la un consens „mai mare”), sau poate avea o părere diferită (şi‑atunci apare o dispută sau o pledoarie, cu unul din preopinenţi reprezentat de grupul iniţial)

2. primii preopinenţi ocupă două locuri în paleta fals‑incert‑adevărat (ei se împart în două tabere, între care există o dispută sau o pledoarie); „noul venit” poate întări una din tabere sau poate ocupa al treilea loc în paletă (caz în care apare o dezbatere)

3. primii preopinenţi ocupă deja toate locurile paletei fals‑incert‑adevărat (sunt trei tabere, între care există o dezbatere); „noul venit” nu are altă şansă decât să realizeze un consens cu una din tabere, întărind‑o.

Acest rezultat se bazează pe numărul limitat de atitudini admise (trei) şi conferă forţă modelului, pentru că îl face aplicabil oricărui număr de preopinenţi, fără a introduce alte tipuri de relaţii în afara disputei, pledoariei, consensului şi dezbaterii.

Partea II – Argumentare

Consideraţii preliminare

Motivele tranziţiei

Absenţa vreunei restricţii privind motivele tranziţiilor constituie una din caracteristicile importante ale modelului pe care‑l propun. Părerile (şi atitudinile) se pot schimba în orice moment şi din orice motiv (răzgândire, revelaţie, inspiraţie etc.), nefiind nici măcar obligatoriu ca elementul declanşator să fi fost produs de partenerul de discuţie[6]. În consecinţă, nu pot studia de ce îşi schimbă preopinenţii părerile, ci pot studia doar ce se întâmplă atunci când ele se modifică.

Nu există „arbitru”

Modelul acordă deci libertate totală preopinenţilor în privinţa părerilor lor – nu există „părere corectă” sau „părere incorectă”, pentru că acceptarea unor asemenea noţiuni ar implica introducerea unui „arbitru absolut”, care să dea verdicte privind corectitudinea părerilor şi, deci, a atitudinilor. Un astfel de „arbitru” este foarte periculos pentru orice model, deoarece alegerea lui corectă (şi chiar existenţa lui) este întotdeauna o problemă dubitabilă, ducând la un model fragil, supus în permanenţă contestaţiilor.

Încercând totuşi definirea unui „arbitru”, acesta poate fi conceput ca un preopinent suplimentar, supus următoarelor restricţii:

(1) Nu emite niciodată enunţuri (are doar atitudini)

(2) Nu are niciodată atitudinea ‚incert’

(3) Nu efectuează niciodată tranziţii (nu-şi schimbă atitudinile)

(4) Atitudinile lui sunt logic coerente (formează un sistem logic ne-contradictoriu)

Ca şi în cazul preopinenţilor obişnuiţi, nu interesează care sunt mecanismele prin care acest „păstrător al adevărului absolut” reuşeşte să-şi definească atitudinile. El poate fi imaginat ca o entitate înzestrată cu un model de judecată necunoscut, care reuşeşte să exprime una din atitudinile ‚fals’ sau ‚adevărat’ în faţa oricărui enunţ, astfel încât să nu se contrazică niciodată. Cu alte cuvinte, dacă faţă de un enunţ are atitudinea ‚adevărat’, atunci trebuie ca din restul enunţurilor acceptate să nu se poată deduce negaţia enunţului. Dacă faţă de un enunţ are atitudinea ‚fals’, trebuie ca din restul enunţurilor acceptate să nu se poată deduce adevărul acelui enunţ. Aşa cum se va vedea mai jos, o altă exprimare a acestei condiţii este ca „arbitrul” să aibă întotdeauna o atitudine logică.

În legătură cu „arbitrul” astfel definit se pun două probleme de importanţă capitală:

1. Fiind dată o discuţie oarecare, este întotdeauna posibilă construirea unui sistem care să respecte condiţiile (1) - (4)?

2. Presupunând că se poate întotdeauna construi un astfel de sistem, este el unic? (Nu există un alt sistem, respectând aceleaşi condiţii, care să aibă însă atitudini diferite de ale primului?)

*** Rămâne să dezvolt aceste două probleme. De introdus demonstraţia cu maimuţa care aruncă cu banul.

Logică. Sisteme de ipoteze. Modele de judecată

Preopinenţii nu pot acţiona pornind de la premisa că celălalt îşi poate schimba părerile oricând şi fără motiv. Acest punct de vedere (anume că nu se pot prevedea atitudinile celuilalt) trebuie asumat numai de către cel ce studiază discuţia, nu şi de preopinenţii înşişi (modelul trebuie să fie obiectiv, în timp ce preopinenţii pot fi – şi sunt – subiectivi).

Experienţa arată că în gândire există nişte mecanisme invariante, care au fost decantate de-a lungul timpului în ceea ce se numeşte logică. Este important de înţeles că principiile logicii acţionează întotdeauna, ca un liant, chiar dacă enunţurile şi ipotezele aparţin unor domenii „mai puţin logice”, cum ar fi etica, morala, estetica etc. Spre exemplu, fundamentul logic al argumentului „Hai te rog, iubiţel” poate fi următorul:

„Dacă eu te iubesc, atunci şi tu mă iubeşti.”

„Eu te iubesc.”

Deci, „Tu mă iubeşti.”

„Dragostea presupune să nu dezamăgeşti persoana iubită.”

„M-ai dezamăgi dacă n-ai face ce-ţi cer.”

Deci, „Trebuie să faci aşa cum îţi cer.”

După cum se vede, mecanismul de articulare a ipotezelor este perfect logic. Particularitatea acestui exemplu constă în aceea că enunţurile aparţin ariei emoţionale. Mai limpede spus, relevanţa, gradul de adevăr al ipotezelor este mare din punct de vedere emoţional. Odată identificat acest punct de vedere, ipotezele se înlănţuie conform principiilor clasice ale logicii. Bineînţeles, un alt punct de vedere, să zicem economic, ar putea să valorizeze mai mult enunţuri de genul „Vom pierde bani dacă fac aşa”, care ar duce la concluzia „Deci, nu trebuie să fac aşa”. Şi acest raţionament este logic. Diferenţa între cele două raţionamente constă în criteriile diferite de valorizare a enunţurilor, mecanismele logice fiind însă aceleaşi. Nu există „o logică a frumosului”, „o logică a dragostei”, „o logică a moralului” şi „o logică pură, rece”, ci există o singură logică, aplicată identic unor enunţuri cernute prin filtre diferite. Numesc aceste filtre sisteme de referinţă. Adăugând fiecărui sistem de referinţă „liantul” numit logică, se obţin diverse sisteme de apreciere şi deducere a adevărului enunţurilor, pe care le numesc modele de judecată.

Modelele de judecată generează atitudini, dar ele permit preopinenţilor şi să facă previziuni sau presupuneri privind schimbările de atitudine pe care un enunţ le va genera. În această secţiune a lucrării mă voi ocupa de componenta logică a modelelor de judecată. Studiul sistemelor de referinţă nu face obiectul acestei lucrări.

Argument

Atitudine logică

Cu toate că nu există vreun „arbitru universal”, atitudinile pot fi comparate cu elemente alese (mai mult sau mai puţin arbitrar) ca referinţă. O posibilitate este compararea unei atitudini cu atitudinea logică pe care cineva ar trebui să o aibă într‑un anume context. De exemplu, dacă cineva este de acord că „A este adevărat” şi că „A implică B este adevărat”, ar fi logic să fie de acord în continuare şi cu „B este adevărat”. Totuşi, în timpul unei discuţii reale, el poate susţine contrariul. Acest comportament nu va descalifica însă discuţia, nu o va face să dispară (preopinenţii ar putea cheltui o mulţime de timp şi energie în discuţie), deci, dacă realitatea acceptă astfel de situaţii, la fel trebuie să facă şi orice model al discuţiei.

Practic, pentru determinarea atitudinii logice a unui preopinent faţă de un enunţ trebuie parcurşi următorii paşi:

1. se determină spaţiul enunţurilor acceptate de preopinentul respectiv

2. se cercetează dacă enunţul cercetat rezultă logic din enunţurile acceptate

3. se cercetează dacă negaţia enunţului cercetat rezultă din enunţurile acceptate

4. dacă s-a putut deduce enunţul cercetat, dar nu şi negaţia lui, atunci atitudinea logică faţă de acel enunţ este ‚adevărat’

5. dacă s-a putut deduce numai negaţia enunţului cercetat, atunci atitudinea logică este ‚fals’

6. dacă nu s-a putut deduce nici enunţul, nici negaţia lui, atunci atitudinea logică este ‚incert’

7. dacă s-au putut deduce atât enunţul, cât şi negaţia lui, atunci este vorba de o contradicţie, iar atitudinea logică nu există

Doi paşi conduc la greutăţi practice majore: paşii 2 şi 3. Dacă se găseşte rapid o demonstraţie a enunţului de cercetat pe baza enunţurilor acceptate, atunci pasul 2 este rezolvat. Dacă însă câteva încercări de demonstrare eşuează, nu se poate trage concluzia că enunţul nu poate fi demonstrat. Pentru aceasta ar trebui epuizate toate încercările de demonstraţie, ceea ce este practic imposibil. Sau ar trebui demonstrat că spaţiul enunţurilor acceptate nu poate demonstra enunţul cercetat, ceea ce este de cele mai multe ori extrem de dificil. Aceleaşi probleme sunt valabile şi pentru negaţia enunţului de cercetat.

De remarcat că sunt posibile situaţii în care nu există atitudine logică faţă de un enunţ. Acestea sunt situaţii în care spaţiul enunţurilor acceptate este un sistem contradictoriu. În aceste situaţii, „vinovat” nu este enunţul cercetat, ci una (unele) din atitudinile precedente ale respectivului preopinent. Testul atitudinii logice nu face în acest caz decât să releve o „hibă logică” pre-existentă. Bineînţeles, spaţiul enunţurilor acceptate de un preopinent poate fi contradictoriu chiar dacă acest lucru nu este relevat de vreun test – e posibil pur şi simplu să nu apară în discuţie enunţul care ar face dovada inconsistenţei.

În cazul în care atitudinea logică există, ea poate coincide sau nu cu atitudinea efectiv exprimată de preopinent – preopinentul este liber să aibă o atitudine diferită de cea logică faţă de un enunţ. Această neconcordanţă conduce la contradicţie, dar discuţia nu „explodează”, nu ajunge în impas, ci continuă practic la fel ca înainte (adică prin aceleaşi mecanisme). Preopinentul „vinovat” de contradicţie ar putea realiza impasul şi ar putea lua măsuri (de exemplu să-şi schimbe atitudinea faţă de un enunţ mai vechi), dar nu este obligatoriu să se întâmple astfel. Modelul schiţat aici nu se bazează pe evoluţia exclusiv logică a discuţiei, ci oferă atitudinea logică doar ca un (posibil) element de raportare.

Baza, structura şi concluzia argumentului

În discuţie apare necesitatea ca un preopinent să sprijine un enunţ –  indiferent de modelul de judecată adoptat, el trebuie să prezinte un set de enunţuri care să aibă drept consecinţă logică enunţul iniţial. Dacă, spre exemplu, X doreşte să justifice enunţul „Dan şi‑a cumpărat o maşină”, el ar putea încerca astfel:

(1) „Dan mi‑a arătat actele maşinii.”

De ce o astfel de declaraţie are drept consecinţă logică faptul că Dan şi‑a cumpărat o maşină? Răspunsul nu este evident atâta timp cât nu se explicitează şi un alt enunţ, pe care preopinentul l‑a considerat implicit:

(2) „Dacă o persoană îmi arată actele unei maşini, atunci acea persoană şi‑a cumpărat maşina respectivă.”

Combinaţia acestor două enunţuri are într‑adevăr drept consecinţă logică enunţul „Dan şi‑a cumpărat o maşină.”

Se observă că al doilea enunţ este o implicaţie logică („Dacă <...ipoteza...>, atunci <...concluzia...>”). Ipoteza seamănă cu enunţul (1), fiind de fapt o generalizare a acestuia (nu se spune „Dan”, ci „o persoană”). Concluzia implicaţiei seamănă cu enunţul care se doreşte a fi susţinut, fiind o generalizare similară a lui. Notând „o persoană” cu x şi introducând deja notaţiile pentru definiţia ce va urma, în diagrama următoare se pot urmări aceste similitudini:

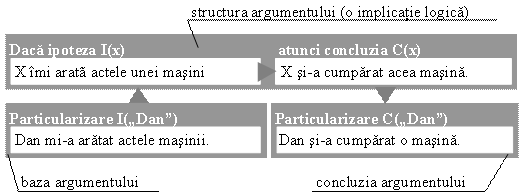
De fapt, preopinentul nu face nişte generalizări ad‑hoc, ci caută o implicaţie cu ipoteză şi concluzie generale, astfel încât o particularizare a ipotezei să‑i fie la îndemână (s‑o poată afirma), iar particularizarea corespunzătoare a concluziei să fie exact enunţul pe care doreşte să‑l susţină. Săgeţile din diagramă nu indică ordinea „descoperirii” enunţurilor, ci evidenţiază doar relaţiile logice dintre ele.

Aceasta este cea mai simplă variantă de susţinere logică a unui enunţ, pe care‑o voi numi argument:

Argument pentru un enunţ C este o conjuncţie logică (o alăturare prin „şi”) a două propoziţii:

‑ structura argumentului: o implicaţie logică de două predicate I(x) Þ C(x), astfel încât o particularizare C(p) a concluziei acestei implicaţii să coincidă cu enunţul ce se doreşte a se argumenta, C, şi

‑ baza argumentului: particularizarea corespunzătoare I(p) a ipotezei implicaţiei.

Enunţul iniţial, C, îl numesc concluzia argumentului.

Este important de observat că printre componentele argumentului nu se numără şi concluzia sa. Într‑adevăr, concluzia argumentului, C, coincide doar cu o particularizare C(p) a lui C(x), care la rândul său nu este decât o parte din structura argumentului.

Structura argumentului poate să nu fie evidentă (de multe ori ea nu este nici măcar explicită). Dar ea este absolut necesară pentru a asigura consistenţa logică a argumentului. Un „test practic de consistenţă” ar putea fi următorul: dacă argumentul poate răspunde la întrebarea „De ce?”, atunci el cuprinde toate elementele logice necesare funcţionării (fără ca aceasta să însemne însă că ele şi funcţionează conform intenţiei autorului – un argument poate fi corect construit, dar baza sau structura lui să fie false, aşa cum şi o haină poate fi admirabil croită, dar din stofă proastă). De fapt, întrebarea „De ce?” este cea mai potrivită pentru a scoate la iveală tocmai structura argumentului.

Mecansimul intern de funcţionare a argumentului. Structura‑p

O analiză mai atentă a componentelor unui argument relevă faptul că, din punctul de vedere al logicii formale, ele nu sunt suficiente pentru a explica funcţionarea lui. Aceasta din cauză că baza este un enunţ particular ce nu se poate substitui pur şi simplu ipotezei structurii (care este un enunţ general). De fapt, inferenţa se desfăşoară în două etape:

‑ din implicaţia generală se deduce o implicaţie particulară, apoi

‑ implicaţia particulară, împreună cu baza, conduc la validitatea concluziei:

„I(x) Þ C(x)”  Þ   „I(p) Þ C(p)” ü

ý Þ „C(p)”

                                             „I(p)”þ

De exemplu:

                 Este adevărat în general că     „Dacă un om e bolnav, atunci suferă.” (structura)

                     Rezultă că, în particular,     „Dacă Popescu e bolnav, atunci suferă.” (structura‑p)

         E Popescu bolnav? Într‑adevăr,     „Popescu e bolnav.” (baza)

                 Deci, conform structurii‑p,     „Popescu suferă.” (concluzia)

Am notat cu structura‑p implicaţia ce se obţine prin particularizarea structurii (la valoarea „Popescu” impusă de bază). Această etapă intermediară, a structurii‑p, este şi ea de multe ori trecută cu vederea, dată fiind evidenţa ei. Totuşi, din punct de vedere logic, ea este absolut necesară. În consecinţă, diagrama elementelor componente ale argumentului se poate completa astfel:

Structura‑p nu a trebuit introdusă prin definiţie, pentru că ea este o consecinţă logică a structurii. Totuşi, chiar neintrodusă prin definiţie, structura‑p este element component al argumentului în aceeaşi măsură ca şi structura sau baza. În ultimă instanţă (aşa cum se vede şi în diagrama de mai sus), structura‑p şi nu structura generală este aceea care permite transferul efectiv de adevăr de la bază la concluzie.

Aşa cum am arătat şi mai devreme, săgeţile din diagrama de mai sus indică ordinea logică a transferurilor de adevăr. Ordinea efectivă de apariţie a „ideilor” în mintea celui care argumentează este probabil cu totul alta, dar acest aspect nu face obiectul lucrării de faţă.

Implicaţii generale şi particulare

În definiţia argumentului, este esenţial faptul că structura este o implicaţie cu caracter universal (adică este generală, se referă la nişte elemente neprecizate). Implicaţiile cu caracter particular nu pot constitui structuri pentru argumente. Totuşi, ar putea spune cineva, implicaţiile particulare ar fi putut fi acceptate şi ele ca structură. Nu am făcut acest lucru pentru că implicaţiile particulare au „forţă” logică extrem de redusă în comparaţie cu implicaţiile universale. Numai particularizarea implicaţiilor universale este un pas semnificativ în raţionament, acest proces câştigându‑şi astfel dreptul de a fi notat printr‑un cuvânt („argument”) şi de a fi studiat.

*** Aici mai trebuie dezvoltat.

Argumentul merge de la general la particular

Un argument poate avea drept concluzie un enunţ oricât de complicat, chiar şi unul de complexitatea şi forţa unei implicaţii universale. Cu toate acestea, argumentul reduce întotdeauna gradul de generalitate (*** vezi „Un exemplu complex”). Acest lucru poate părea restrictiv – nu există oare şi argumente care nu reduc generalitatea, ci o păstrează la nivel constant (fie el general sau particular), sau chiar merg invers, de la particular la general? La o analiză atentă, orice exemplu (aparent) de acest gen se dovedeşte a se baza totuşi pe o implicaţie generală, care se particularizează (treptat sau dintr‑o dată). Această „coborâre” de la (foarte) general la (mai) particular constituie însăşi esenţa procesului de argumentare.

*** şi aici mai trebuie dezvoltat.

Susţinere şi contra‑argument. Negaţie

Dat fiind un argument A şi concluzia lui C, numesc susţinere perecehea argument-concluzie: (A, C). Contra‑argument este un argument A’ având drept concluzie negaţia logică a enunţului C (voi nota negaţia cu ¬C). Evident, contra-susţinere este perechea (A’, ¬C). Denumirea este sugestivă şi face definiţia uşor de reţinut: contra‑argumentul are concluzie contrară argumentului.

Deşi contra‑argumentul ar părea că se opune unei încercări de susţinere a unui enunţ, el nu este „distructiv” sau „negativist” în comparaţie cu argumentul, pentru că, în fond, ambele încearcă să susţină nişte enunţuri (care, întâmplător, se află în relaţie logică de negare). Prezenţa negaţiei într‑un enunţ nu îndreptăţeşte părerea că el ar fi „negativ” (dintre „Aici e vid” şi „Nu e vid, există o mulţime de particule”, care enunţ e mai „negativ”?). De fapt, nici nu există enunţuri negative în sine, ci doar perechi de enunţuri în relaţie logică de opoziţie, de negare reciprocă.

Obiecţie. Contestaţie

Fie un argument A, format din baza B şi structura S. Numesc obiecţie negaţia argumentului A.

Cum argumentul înseamnă conjuncţia „B şi S”, negaţia lui va fi negaţia acestei conjuncţii. Negaţia unei conjuncţii este o disjuncţie, deci, notând negaţia bazei cu ¬B şi negaţia structurii cu ¬S, obiecţia va fi „¬B sau ¬S”. Practic, dat fiind că atât ¬B singură, cât şi ¬S singură fac disjuncţia să fie adevărată, voi numi aceste negaţii:

‑ negaţia bazei unui argument este obiecţie la bază (¬B)

‑ negaţia structurii unui argument este obiecţie la structură (¬S).

Spre deosebire de argument şi contra‑argument, care sunt structuri logice (relativ) complexe, obiecţia este o simplă negaţie logică. Dacă obiecţia este însă argumentată, atunci ia naştere o contestaţie. Cu alte cuvinte, contestaţia este un argument ce are drept concluzie negaţia unui alt argument (concluzia contestaţiei este o obiecţie la acel argument). Bineînţeles, există contestaţie a bazei şi contestaţie a structurii.

Din punct de vedere grafic, voi reprezenta un argument astfel:

Cu aceasta, noţiunile introduse până acum se pot reprezenta sintetic în următoarea diagramă:

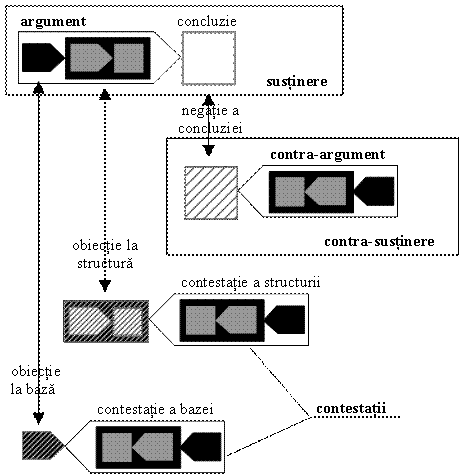
Motorul logic al argumentării

Principiul general al argumentării

Pentru ca din elementele argumentului să rezulte concluzia sa este necesar un pas logic pe care nu l‑am evidenţiat până acum, pentru că el pare evident. Este vorba totuşi de un pas logic foarte important, pe care‑l numesc principiul general al argumentării:

Dacă un argument este adevărat (adică atât baza, cât şi structura lui sunt adevărate), atunci concluzia lui este adevărată.

Evidenţa acestui principiu îl face greu de recunoscut în practică, pentru că, de cele mai multe ori, preopinenţii transferă adevărul în mod automat şi inconştient de la componentele argumentului către concluzia sa.

De fapt, principiul general al argumentării nu este altceva decât regula logică modus ponens:

Dacă structura‑p este adevărată:    „I(p) Þ C(p)”

                          şi baza este adevărată:    „I(p)”,

atunci concluzia este adevărată:    „C(p)”.

Aşa cum observam şi mai devreme, transferul de adevăr de la bază la concluzie se face prin structura‑p (care, la rândul ei, este o consecinţă directă a structurii argumentului).

Contestaţia (sau obiecţia) nu poate fi contra‑argument

Baza falsă nu conduce la concluzie falsă

Foarte important este că, deşi implicaţia transferă adevărul, ea nu transferă falsitatea. Cu alte cuvinte, dacă într‑o implicaţie (validă) se introduce o ipoteză falsă, nu rezultă o concluzie falsă. Fie următorul caz, în care cineva încearcă să demonstreze falsitatea concluziei pornind de la o obiecţie adusă bazei:

            Sunt de acord că     „Dacă un om e bolnav, atunci suferă.” (structură acceptată)

        şi, deci, accept şi că     „Dacă Popescu e bolnav, atunci suferă.” (structură‑p acceptată)

                   Dar greşeşti,     „Popescu nu e bolnav.” (obiecţie la bază)

                             Deci,     „Popescu nu suferă.” (concluzie incorectă!)

Evident, concluzia este incorectă (Popescu ar putea să sufere şi dacă nu e bolnav – de exemplu din dragoste, sau fiindcă‑l rod pantofii, sau fiindcă şi‑a pierdut slujba etc.). Faptul că ipoteza implicaţiei este (considerată) greşită nu îndreptăţeşte ideea că şi concluzia ei trebuie să fie greşită.

Nici structura falsă nu conduce la concluzie falsă

Negarea structurii unui argument înseamnă negarea implicaţiei generale I(x) Þ C(x). Una din modalităţile de infirmare a unei implicaţii generale este aducerea unui contraexemplu, iar cel mai la îndemână contraexemplu este negarea structurii-p. Dacă un preopinent neagă structura-p, atunci el nu acceptă implicaţia I(p) Þ C(p) (obiecţie înseamnă doar negare, nu şi propunerea unei alte variante!). Conform principiului general al argumentării, conjuncţia „(I(p) Þ C(p)) şi I(p)” devine falsă şi – cum falsul implică orice – rezultă că nu se poate spune nimic despre concluzia C(p).

Dacă structura generală I(x) Þ C(x) este negată prin alte mijloace, atunci consecinţa ei, structura-p, are valoare de adevăr indeterminată şi există cu atât mai puţine motive de a deduce ceva privind concluzia.

Iată deci că invalidarea (prin orice mijloace) a structurii unui argument nu demonstrează falsitatea concluziei lui.

Distrugerea unui argument nu invalidează concluzia lui

Reluând schema de funcţionare a argumentului, se pot identifica două implicaţii al căror adevăr nu poate fi pus la îndoială:

                           particularizarea implicaţiei generale

¯

„I(x) Þ C(x)”  Þ   „I(p) Þ C(p)” ü

ý Þ „C(p)”

                                             „I(p)”þ   

                                                             principiul fundamental al argumentării

                                                             (modus ponens)

Acceptând aceste două implicaţii ca incontestabile, rămân trei elemente prin negarea cărora s-ar putea încerca demonstrarea falsităţii concluziei:

          structura                    structura-p

¯                           ¯

„I(x) Þ C(x)”  Þ   „I(p) Þ C(p)” ü

ý Þ „C(p)”

                                             „I(p)”þ

                                                 baza

După cum am văzut, negarea nici unuia dintre ele nu demonstrează falsitatea concluziei. Rezultă că, în general, nu este adevărată implicaţia: „Dacă un argument este greşit (structura sau baza lui sunt false), atunci concluzia sa este greşită.”

Se observă că, de fapt, această implicaţie încearcă să atace concluzia unui argument (deci să aducă un contra‑argument) printr‑o obiecţie (care, dacă e susţinută, este o contestaţie a argumentului). În consecinţă, trebuie reţinut că o contestaţie (sau o simplă obiecţie) adusă unui argument nu poate juca rol de contra‑argument. Mai limpede: dacă arăt că argumentul lui X este greşit, aceasta înseamnă doar că modul particular ales de X pentru a-şi susţine ideea este incorect – concluzia lui X poate foarte bine să fie corectă, chiar dacă el nu s-a priceput s-o susţină. (Metaforic vorbind, contestând faptul că acest drum ar duce la Paris, nu demonstrez că Parisul nu există.)

Combaterea unei susţineri

Prin atacarea argumentată a concluziei unui argument, cineva încearcă să arate că acea propoziţie (concluzia) este falsă. Acest fapt nu poate înclina „balanţa adevărului” în nici o parte, pentru că situaţia este simetrică şi echilibrată: despre concluzie, un argument susţine că este adevărată, celălalt că este falsă. În esenţă, situaţia este aceeaşi cu afirmarea ne-argumentată a propoziţiei, respectiv a negaţiei ei, de către cei doi preopinenţi.

De exemplu, dacă iniţial X şi Y afirmau că „Ionescu şi-a cumpărat o maşină”, respectiv că „Ionescu nu şi-a cumpărat o maşină”, este evident că ei se află într-o situaţie simetrică. Dacă ulterior fiecare îşi argumentează poziţia („Mi-a spus Cristina”, respectiv „Mi-a spus Mihaela”), simetria rămâne neschimbată: nici una dintre concluzii nu se poate impune asupra celeilalte.

Deci, un contra-argument nu poate combate o susţinere.

Mai sus am arătat că simpla contestare a unui argument nu-i invalidează concluzia, deci nici contestaţia nu poate combate o susţinere.

Pentru mai buna înţelegere, din nou o metaforă: Doi oameni se luptă pe o bârnă, iar cel care cade pierde; evident, pentru a învinge în această probă nu este suficient să-ţi menţii echilibrul (întărirea propriei poziţii, opuse celuilalt = contra-argumentare), ci mai trebuie şi să încerci să-l dezechilibrezi pe adversar (atac asupra „punctelor de sprijin” ale celuilalt = contestaţie). Dacă cei doi n-ar proceda astfel, ei ar sta la nesfârşit pe bârnă, fiecare într-un echilibru de nezdruncinat, şi nimeni n-ar câştiga vreodată, oricât s-ar încorda.

Rezultă că singura metodă logică de a combate o susţinere este atacarea simultană a ambelor ei elemente: un contra-argument va susţine contrariul concluziei, iar o contestaţie va „demonta” argumentul care susţinea concluzia, arătând că el este greşit (şi unde anume este greşeala!). Orice demers care realizează mai puţin de atât este logic incomplet.

Argumentele în lumea reală

„Forţa” unui argument. Dificultăţi teoretice şi practice

Cineva ar putea spune că, aşa cum în cazul a doi oameni care trag de o frânghie, cel cu forţă mai mare va învinge, un argument „mai puternic” va învinge unul „mai slab”. Problema este că nu există vreo definiţie acceptabilă a „forţei” unui argument. Singurul criteriu posibil este „capacitatea de convingere”, cu alte cuvinte „capacitatea de a declanşa o schimbare de opinie” – or, aşa cum am arătat mai devreme, motivele posibile ale schimbării de opinie nu pot fi cuantificate, măsurate şi studiate decât într-o manieră aproximativă (eventual statistică). Nu se poate afirma decât că „Pentru cutare persoană, în cutare situaţie, având cutare model de judecată, argumentul acesta are şanse destul de mari să declanşeze o schimbare de opinie.” O verificare sau o infirmare a acestei afirmaţii este imposibilă, pentru că „şanse destul de mari” exprimă de fapt o probabilitate, iar valoarea unei probabilităţi nu poate fi verificată printr-o singură experienţă (evident, un set de N exerienţe este absurd de conceput – cum aş putea să-i aduc lui X de N ori acelaşi argument, în aceleaşi condiţii, şi să număr de câte ori a avut efect şi de câte ori nu?). Este adevărat, mai multe experienţe se pot face pe N subiecţi, dar în acest caz condiţiile nu mai sunt identice (diferă atât condiţiile fizice externe, cât şi – mai ales – datele culturale, psihice, emoţionale etc. ale fiecărui subiect), ceea ce face (aproape) irelevantă orice concluzie.

Argumentele nu pot fi deci comparate la modul absolut. Totuşi, ele pot fi comparate din diverse puncte de vedere (corectitudine logică, sistem de referinţă etc.), iar instrumentele şi criteriile de comparare sunt puse la dispoziţie de disciplinele respective (logica, psihologia, etica etc.). Chiar şi pentru o comparaţie dintr-un punct de vedere particular (emoţional, de exemplu), disciplina respectivă (psihologia) poate da numai o predicţie probabilistică, bazată pe un model – ceea ce ridică două probleme practice:

1. O predicţie probabilistică nu înseamnă că argumentul va convinge, ci că e posibil să convingă sau nu, fiecare din variante cu o anume probabilitate de realizare. Chiar dacă probabilitatea de convingere este foarte mare, aceasta nu va împiedica persoana concretă X să se încăpăţâneze în a nu se lăsa convinsă – deci argumentul poate foarte bine să eşueze.

2. O predicţie bazată pe un model cere şi verificarea adecvării situaţiei concrete la modelul respectiv. Or, acest lucru este dificil de realizat în practică (de exemplu, ştiu cu precizie maximă că un om dominat de teama de întuneric va accepta argumentul meu, dar nu ştiu cât de teamă îi este lui X de întuneric). Aceată imprecizie în determinarea modelului corect duce la o scădere suplimentară a încrederii în predicţie. Oricum, mijloacele de verificare a adecvării la model aparţin disciplinei care propune modelul şi nu fac obiectul lucrării de faţă.

Singurul numitor comun este logica, dar, cum logica lucrează cu numai două valori de adevăr, rezultatul unei comparaţii între două argumente poate avea doar un grad minim de relevanţă: ambele argumente sunt logic corecte, ambele sunt logic incorecte, sau unul e logic corect iar celălalt nu. Aprecieri mai nuanţate nu sunt posibile folosind logica tradiţională (nu există argumente „mai logice” şi „mai puţin logice”).

Implicaţie şi negare. Insuficienţe ale limbajului

Limbajul[7] traduce negaţia logică prin adverbul „nu”, care se alătură verbelor. Implicaţia este însă greoi redată în limbajul curent, prin cuvintele „dacă” şi „atunci”. Pe lângă faptul că nu există vreun verb căruia să i se poată aplica negaţia, „dacă” şi „atunci” mai apar şi separate unul de altul (prin ipoteza implicaţiei), ele neformând nici măcar o unitate sintactică susceptibilă de a fi negată:

(1) „Dacă are loc I, atunci are loc C.”

Există două verbe cărora li se poate aplica negaţia, deci trei posibilităţi:

(2) „Dacă nu are loc I, atunci are loc C” sau

(3) „Dacă are loc I, atunci nu are loc C” sau

(4) „Dacă nu are loc I, atunci nu are loc C.”

Dacă un vorbitor nu este de acord cu ipoteza I (deşi acceptă implicaţia), el ar putea crede că versiunile (2) şi (4) reflectă punctul lui de vedere (pentru că ele conţin negaţii lingvistice ale ipotezei). Mai ales versiunea „Dacă nu are loc I, atunci nu are loc C” are şanse să‑l atragă.

Un vorbitor care nu este mulţumit cu concluzia C va fi atras de versiunile (3) şi (4) – ele conţin negaţii lingvistice ale concluziei.

Variantele (2) şi (3) par (din punct de vedere al limbajului) a fi negaţii ale implicaţiei (1): „Dimpotrivă, C se întâmplă exact când nu are loc I, nicidecum atunci când are loc”, respectiv „Dimpotrivă, când se petrece I, C este întotdeauna absent, nu prezent.”

Varianta (4) mai pare a fi şi o echivalentă a implicaţiei iniţiale (pentru că, „la bun simţ”, două negaţii se anulează reciproc). Aceasta l-ar putea tenta pe un vorbitor care doreşte să arate că acceptarea implicaţiei (1) conduce la nişte consecinţe absurde. Astfel, el va arăta că forma (4) conduce la absurdităţi şi, crezând că ea este evhivalentă cu (1), va fi convins că a demonstrat că (1) este falsă.

Toate aceste poziţii sunt greşite din punct de vedere logic:

‑ negaţia unei implicaţii nu este o implicaţie, deci nu se poate exprima în termeni de „dacă... atunci”; rezultă că nici una din variantele (2), (3) sau (4) nu poate fi negaţia implicaţiei (1)

‑ dacă ipoteza unei implicaţii este falsă, nu se poate spune nimic despre concluzia ei (ea poate fi adevărată sau nu); în consecinţă, orice implicaţie care deduce adevărul (sau falsitatea) concluziei din falsitatea ipotezei este greşită

‑ falsitatea concluziei este singura care conduce la o implicaţie; aceasta este însă diferită de oricare din variantele (2), (3) sau (4), ea constituindu-se într-o implicaţie „inversată”:

(5) „Dacă nu are loc C, atunci nu are loc I.”

Această implicaţie este dealtfel şi o echivalentă a implicaţiei (1) (singura implicaţie echivalentă logic corectă!).

Totuşi, dacă implicaţiile (2), (3) şi (4) nu reprezintă nici negaţia implicaţiei (1), nici a ipotezei şi nici a concluziei ei, ce legătură logică au cu (1)? Răspunsul este: nici una.

Evitarea capcanelor limbajului

Există forme de exprimare ale implicaţiei care evită pericolele arătate mai sus. Acestea presupun condensarea implicaţiei într-un singur cuvânt, susceptibil de a fi negat. Un exemplu ar fi chiar „A implică B”, dar acesta are neajunsul că negaţia „A nu implică B” nu face evident înţelesul negaţiei.

Altă posibilitate este folosirea expresiilor „toţi”, „întotdeauna”, „ori de câte ori” etc. – nu întâmplător, formularea clasică a silogismelor foloseşte exprimări de genul „toţi A sunt B”. Avantajul este că negaţiile pur lingvistice „nu toţi A sunt B”, „nu întotdeauna când se întâmplă A, urmează B” sau „nu ori de câte ori apare A, apare şi B” exprimă fidel negaţia logică a implicaţiei, care este aceea că „există şi B fără A”. Această ultimă expresie conduce dealtfel şi la o reformulare (lingvistic negativă) a implicaţiei: „nu există B fără A”.

Iată, în rezumat, câteva din posibilităţile de exprimare a implicaţiei şi a negaţiei ei:

implicaţie (AÞB)	negaţia implicaţiei
dacă A, atunci B	–
B dacă A	–
A implică B	A nu implică B
toţi A sunt B	nu toţi A sunt B
întotdeauna câd A, B	nu întotdeauna câd A, B
ori de câte ori A, B	nu ori de câte ori A, B
nu există B fără A	există B fără A
nu se poate B fără A	se poate B fără A

Am evidenţiat exprimările cele mai limpezi şi mai puţin susceptibile de a genera erori prin negare.

Nuanţarea implicaţiei şi a negaţiei ei

Formulele de tipul „toţi A sunt B”, respectiv „nu toţi A sunt B” funcţionează bine numai raportate la o logică bipolară. De exemplu, dacă cineva afirmă „Toţi oamenii doresc să trăiască mai bine”, pare să aibă dreptate. Totuşi, dacă altcineva contra-argumentează „Eu cunosc un bolnav psihic care nu doreşte să trăiască mai bine, deci iată că nu absolut toţi oamenii doresc să trăiască mai bine”, şi acesta pare să aibă dreptate. Problema este că, de multe ori, „toţi” nu este înţeles la modul absolut, ci mai degrabă ca „aproape toţi”, „majoritatea” etc. La fel, şi „nu toţi” poate însemna de la „Ei haide, nu chiar toţi, o mai fi unul care nu...” până la „Toţi? Aiurea! Poate unul, maxim doi, care să...” sau chiar „Fals! Nici unul nu...” O asemenea accepţiune „vagă” nu este neapărat greşită, dar ea poate funcţiona numai în cazul raportării la o logică nuanţată, care acceptă grade diferite de adevăr, intermediare valorilor „absolut adevărat” şi „cum nu se poate mai fals”. Dacă unul dintre preopinenţi cântăreşte afirmaţia cu o măsură logică nuanţată, iar celălalt cu o măsură logică bivalentă, discuţia dintre ei nu are mai mult sens decât discuţia dintre un vietnamez şi un norvegian, fiecare vorbind pe limba lui.

În concluzie, dacă un preopinent foloseşte o implicaţie în sens vag, nuanţat, e bine să precizeze explicit aceasta, prin expresii de tipul „aproape toţi”, „foarte mulţi”, „majoritatea”, „o mare parte”, „de obicei”, „de regulă”, „de cele mai multe ori”, „adeseori”, etc. (sau „nu prea”, „arareori” etc. – în cazul formulărilor lingvistic negative ale implicaţiei). În lipsa unor astfel de nuanţe explicite, implicaţiile trebuie înţelese în sensul absolut, iar cel care le foloseşte trebuie să-şi asume consecinţele (logice) ale acestui sens.

Implicaţia şi relaţia cauză-efect

Implicaţia este de multe ori confundată cu relaţia cauză-efect. Acesta nu este neapărat un neajuns al limbajului (exprimările „dacă A, atunci B” şi „din cauză că A, se întâmplă B”, deşi oarecum asemănătoare, sunt totuşi clar diferite), ci este mai degrabă expresia reflexului fundamental de asociere care stă la baza inteligenţei. Înţelegerea relaţiei cauză-efect între fenomenele A şi B este precedată de obicei de observaţia că „întotdeauna când se întâmplă A, urmează B”. Aceasta din urmă nu este altceva decât implicaţia logică AÞB, în formularea cu „întotdeauna”. Esenţa implicaţiei nu este una cauzală, ci simpla observare a apariţiei fenomenelor A şi B. Implicaţia nu explică nimic, nu arată motivele pentru care se întâmplă aşa şi nu altfel, ea este un simplu instrument de consemnare a unei observaţii de natură statistică[8].

Confundarea implicaţiei cu o relaţie cauzală este periculoasă din două puncte de vedere: Întâi pentru că a „descoperi” explicaţii acolo unde nu există relaţii cauză-efect este dăunător procesului de înţelegere şi poate duce la concluzii greşite (Exemplu: „De fiecare dată când văd lumina fulgerului, în curând aud şi tunetul” versus „Lumina fulgerului este cauza tunetului” – implicaţia este adevărată, dar fenomenele nu sunt unul cauză şi celălalt efect, ci ambele sunt efecte ale cauzei comune, descărcarea electrică atmosferică). Al doilea pericol este ca, în faţa afirmaţiei „A implică B”, un preopinent să fie deranjat de ideea asociată că „A este cauză pentru B” şi să-şi concentreze eforturile înspre demonstrarea faptului că A nu este cauză pentru B, deşi nimeni n-a afirmat acest lucru.

Confuzia cu echivalenţa. Altă insuficienţă a limbajului

Echivalenţa este o implicaţie reciprocă: „A Û B” înseamnă „A Þ B şi B Þ A”. O proprietate importantă a echivalenţei este că transferă atât adevărul, cât şi falsitatea: din „A este echivalent cu B” rezultă „dacă A este adevărat, atunci B este adevărat”, dar şi „dacă A este fals, atunci B este fals”.

Această proprietate a echivalenţei explică de ce se crede uneori că falsitatea ipotezei unei implicaţii ar conduce la falsitatea concluziei ei: se confundă pur şi simplu implicaţia simplă cu o implicaţie reciprocă (echivalenţă). De exemplu, când mama îi spune copilului „Dacă mănânci tot, primeşti desert”, iar copilul vede că refuzând să mănânce tot, nu primeşte desert, el îşi formează ideea că afirmaţia mamei implică „Dacă nu mănânci tot, nu primeşti desert”. Această implicaţie este adevărată, dar nu din cauză că ar decurge logic din prima, ci din cauză că intenţia mamei a fost să exprime o echivalenţă: „Dacă mănânci tot, primeşti desert, iar dacă nu mănânci tot, nu primeşti.” Fără discuţie, exprimarea este lungă, greoaie şi pare (dar nu este!) redundantă, ceea ce îi face pe mulţi vorbitori s-o prescurteze. Astfel se face că echivalenţa şi implicaţia ajung să fie confundate una cu alta, efectul cel mai neplăcut fiind transferul nejustificat al proprietăţii „Dacă nu..., atunci nu...” de la echivalenţă la implicaţie.

Din păcate, pentru echivalenţă nu există în vorbirea curentă formulări mai sintetice. „A este echivalent cu B” nu este adecvată („A mânca tot este echivalent cu a primi desert” sună greoi), iar formulările din matematică „dacă şi numai dacă” (prescurtată uneori „ddacă”) sau „necesar şi suficient” nu au fost adoptate pe scară largă în vorbirea curentă. Singura variantă acceptabilă este „numai dacă”, dar din păcate ea nu este folosită atât de frecvent pe cât ar trebui.

De ce logică bipolară?

Limbajul este guvernat de logica bipolară

Procesele reale de gândire operează în esenţă cu noţiuni vagi. Cu toate acestea, structura limbajului este mai degrabă precisă, dihotomică, bipolară. Există mijloace prin care procesele reale de comunicare pot transmite într-o oarecare măsură nuanţarea proceselor de gândire (intonaţia, accentul, mimica etc.), dar acestea se împuţinează pe măsură ce comunicarea se „universalizează”. De exemplu, mesajele ambigui, nuanţate, pot fi transmise relativ uşor într-o discuţie între soţ şi soţie, pentru că se poate presupune o cunoaştere reciprocă a modurilor lor de gândire – dar „limbajul” lor este foarte intim, adaptat comunicării numai între ei doi, şi transpus în exteriorul cuplului ar da rezultate nesatisfăcătoare. Cum scopul limbii nu este comunicarea doar între perechi de oameni, ci (la limită) între oricare doi oameni dintr-o colectivitate, ea trebuie să fie cât mai universală, să se perfecţioneze în transmiterea exact a acelor procese de gândire care funcţionează identic la toţi oamenii. Limbajul matematic, de exemplu, ajunge să depăşească până şi graniţele cultural-lingvistice (o teoremă scrisă de un matematician maghiar are şanse maxime de a fi înţeleasă imediat de un matematician indian, chiar dacă nici unul nu cunoaşte limba celuilalt). Aspiraţia de universalitate a limbii conduce aşadar la diminuarea nuanţării, apropiind mecanismele logice ale limbii de logica bipolară.

Este adevărat că inovaţia, descoperirea sau creaţia nu pot fi concepute fără nuanţare, intuiţie etc., dar acesta sunt procese de gândire esenţialmente intime, personale, şi nu colective. Pe de altă parte, discuţia în general, ca proces de comunicare, şi disputa în particular se sprijină tocmai pe caracterul precis, bipolar al limbii, caracter ce derivă din universalitatea ei.

Acesta este motivul pentru care am optat în această lucrare pentru logica tradiţională: dacă limba este guvernată de logica bipolară, atunci un model al discuţiei riscă să se îndepărteze de fenomenul studiat dacă se bazează pe o logică nuanţată.

Problemele logicilor nuanţate

Totuşi, odată ce logicile nuanţate conţin ca un caz particular logica bipolară „clasică”, n‑ar fi oare mai nimerit să se studieze disputa, discuţia în general, utilizând un model logic nuanţat, mai general? Răspunsul este în continuare nu, deoarece logicile nuanţate se bazează pe un parametru cantitativ, numeric, care, deşi potrivit pentru teoretizare, este inadecvat studiului unui fenomen care implică subiecţi umani. Oricare ar fi acest parametru („grad de încredere”, „probabilitate”, „relevanţă”, „grad de apartenenţă la o mulţime fuzzy” etc.), el nu poate fi determinat niciodată cu exactitate în cazul unui preopinent.

Teoremele, formulele şi rezultatele unei logici nuanţate, cantitative, sunt întotdeauna propoziţii „absolut adevărate”, aparţinând logicii clasice, bipolare (ar fi absurd de conceput o teorie ştiinţifică, indiferent la ce s-ar referi ea, ale cărei propoziţii să fie „aproximativ adevărate”). De exemplu, o formulă ar putea suna astfel: „Dacă gradul de încredere în implicaţia A Þ B este x şi gradul de încredere în propoziţia A este y, atunci gradul de încredere în propoziţia B este x*y”. Utilitatea unei astfel de formule este însă nulă atâta timp cât nu se pot determina valorile x şi y. Singura abordare care ar avea şanse de reuşită ar fi una probabilistă, în care x şi y să fie variabile aleatoare. Dar o abordare probabilistă poate fi aplicată numai unui număr mare de experimente, ceea ce, aşa cum arătam mai devreme, este imposibil de imaginat în cazul discuţiilor între oameni (din cauza multitudinii factorilor variabili şi incontrolabili – background cultural, stare de spirit momentană, nivel de educaţie, capacitate de concentrare etc.).

Chiar dacă se pot imagina metode statistice satisfăcătoare care să folosească o logică nuanţată, cantitativă, am optat în această lucrare pentru un model logic clasic, calitativ, pentru că nuanţarea care apare uneori în discuţiile dintre oameni poate fi lesne analizată cu logica tradiţională folosind în loc de „toţi” exprimări de genul „foarte mulţi”, „marea majoritate” etc., sau chiar exprimări cantitative, de tipul „87%”. Astfel, o eventuală dispută cu subiectul „87% dintre oameni doresc să trăiască mai bine” poate fi foarte bine studiată analizând cu logica tradiţională propoziţiile „87% din oameni doresc să trăiască mai bine” şi „nu este adevărat că 87% din oameni doresc să trăiască mai bine”. Este adevărat că nici procentele şi nici sensurile exprimărilor „foarte mulţi” sau „marea majoritate” nu pot fi determinate cu exactitate, dar, odată ce logicile nuanţate perpetuează exact acest neajuns major, camuflându-l în loc să-l rezolve, ce rost ar avea apelul la ele?

Mai mult chiar, abordarea clasică este mai tolerantă decât logicile nuanţate, pentru că doi preopinenţi pot fi de acord unul cu altul că „foarte mulţi oameni...”, deşi prin „foarte mulţi” unul înţelege „peste 80%”, iar celălalt „peste 90%” – ambii fiind însă de acord cu afirmaţia, diferenţa nu mai contează. Într-o logică nuanţată însă, această diferenţă nu ar putea fi trecută cu vederea, impasul inegalităţii (şi indeterminării) numerice perfecte fiind prezent încă de la început chiar şi în cele mai simple situaţii. Dacă pe parcursul discuţiei, prin consecinţele acceptării afirmaţiei de mai sus, diferenţa de apreciere dintre cei doi preopinenţi devine relevantă, logica tradiţională tranşează foarte simplu problema prin analiza enunţurilor „«foarte mulţi» înseamnă «peste 80%»”, respectiv „«foarte mulţi» înseamnă «peste 90%»”. De fapt, aceste enunţuri sunt definiţii, iar definiţia va fi tratată în capitolul următor.

Definiţie

Rolul definiţiei

Aşa cum am arătat, procesul de argumentare se bazează pe deducerea particularului din universal. Pentru a opera însă cu universalul, în practică se dovedesc utile unele „prescurtări” ale exprimării, care condensează ideile. Ideea de „prescurtare” a universalului nu este legată neapărat de argumentare, ci este folosită oriunde apare necesitatea operării cu universalul (cercetare, explicare etc.).

Definiţia nu poate fi falsă

Din punctul de vedere al logicii, definiţiile sunt în general la libera alegere a celor care le dau, pentru că ele nu sunt rezultatul unor judecăţi, ci sunt convenţii. Acest lucru se observă cel mai limpede dacă se pune întrebarea „De ce?” vizavi de o definiţie – singurul răspuns posibil este „Pentru că aşa vreau eu.”[9]

Fiind o convenţie, definiţia nu poate fi falsă. Absurditatea punerii problemei falsităţii unei definiţii se observă mai uşor dacă se foloseşte persoana întâia singular: „Numesc triunghi o mulţime de trei puncte.” Cum ar putea această propoziţie să fie falsă? Ar însemna ca preopinentul să mintă când afirmă aceasta, adică de fapt el să nu numească „triunghi” o mulţime de trei puncte. Continuarea raţionametului pe această linie este evident absurdă şi neproductivă, odată ce nu se poate niciodată sonda mintea lui, pentru a şti dacă e sincer sau nu când afirmă că foloseşte această convenţie.

De fapt, folosirea persoanei întâia singular este obligatorie într-o definiţie – altfel, enunţul nu mai este o convenţie, ci afirmă faptul că o colectivitate oarecare acceptă acea convenţie (ceea ce este întotdeauna dubitabil). Spre exemplu, „oamenii înţeleg prin «compas» un instrument pentru desenat cercuri” nu este o definiţie, ci afirmă că toţi oamenii acceptă definiţia „«compas» este un instrument pentru desenat cercuri”. Or, acest lucru este fals, pentru că unii oameni (englezii) înţeleg prin «compas» un instrument cu ac magnetic pentru determinarea nordului (busolă). Corect ar fi deci să se spună „Eu înţeleg prin «compas» un instrument pentru desenat cercuri”, rămânând la latitudinea celuilalt dacă să accepte această definiţie sau nu.

Pentru că limbajul trebuie să servească comunicării între cât mai mulţi oameni, este necesar un set coerent şi consistent de definiţii, care să fie acceptate de membrii unei comunităţi. De aceea se alcătuiesc de exemplu dicţionare, în care scrie „compas = instrument pentru desenat cercuri”. Semnul „=” reprezintă o recomandare, în sensul „Pentru ca noi, românii, să ne înţelegem unii cu alţii, ar fi bine să folosim cu toţii «compas» în sensul de «un instrument pentru desenat cercuri».” Afirmaţia că recomandarea, norma, este aceasta şi nu alta este o propoziţie care poate fi adevărată sau falsă, spre deosebire de definiţie, care nu poate fi decât adevărată. (Exemplu: „Numesc «triunghi» o mulţime de trei segmente’ „Bine, te cred pe cuvânt că asta înţelegi tu prin «triunghi»” versus „În geometrie, «triunghi» înseamnă o mulţime de trei segmente” „Greşit! Iată manualul de geometrie, care spune că «triunghi» înseamnă o mulţime de trei puncte!”)

A rejecta o definiţie, a nu o accepta, nu înseamnă a o eticheta cu ‚fals’, ci exprimă doar faptul că preopinentul nu doreşte să folosească în discuţie respectiva convenţie. Motivele pentru care ar putea refuza acest lucru nu au o justificare strict logică, ci ţin eventual de comoditate („M-am obişnuit să înţeleg prin «compas» un instrument pentru determinarea nordului magnetic, aşa că mi-ar fi greu să-ţi urmăresc raţionamentele dacă aş accepta altă definiţie”).

*** Aici am rămas. În continuare voi schiţa planul capitolelor următoare.

Ce este definiţia

...

Sinonimia

...

Omonimia

...

Tipuri de contestaţii

Reducerea la absurd

...

Contra-exemplul

...

Surse de erori

Erori în discuţie

Distincţia dispută/pledoarie

...

Victoria în sub-dispută

...

Identificarea subiectului

Să presupunem că X susţine ideea C prin argumentul „B şi (B Þ C)”. Y ar putea să nu fie de acord cu unul din elementele argumentaţiei lui X şi astfel, prin contestarea acelui element (fie el baza, B), să se nască o dispută. Aceasta nu este o sub‑dispută, ci singura şi reala dispută – pentru că nu există vreo contestare a concluziei C, ci doar a bazei argumentului. X, simţind împotrivire, crede că Y nu e de acord cu concluzia, deci – din punctul lui de vedere – subiectul este ?C. Din punctul de vedere al lui Y, subiectul este (cel puţin la început) ?B. În acest fel, se poate pierde foarte mult timp şi nervi, pentru ca în final să se ajungă la concluzia că propoziţia C este adevărată, dar argumentaţia corectă nu este cea susţinută de X (bazîndu‑se pe B), ci alta. Această concluzie este cazul fericit, pentru că de multe ori Y îşi foloseşte (conştient sau nu) victoria in disputa ?B pentru a clama că a cîştigat disputa ?C.

Distincţia dispută simplă/dispute asociate

...

Identificarea concordanţelor şi a discordanţelor

O problemă foarte delicată este corecta identificare a pivotului unor dispute asociate. În exemplul de mai sus, unde A şi B purtau două dispute asociate cu pivotul „Ionescu şi‑a cumpărat o maşină marca x”, pivotul general este „Y a făcut acţiunea z relativ la obiectul t, marca x”, unde Y parcurge o mulţime de persoane, z poate fi „a cumpărat”, dar şi „a închiriat”, „a furat” etc., t poate fi „o maşină”, dar şi „o bicicletă” sau „un camion”, iar x poate parcurge o mulţime de mărci. În timpul unei dispute se poate întâmpla ca cei doi preopinenţi să înţeleagă diferit care din elementele pivotului general sunt valide şi care sunt contestate.

Negarea definiţiei

...

Sinonimia

Se poate întîmpla ca preopinenţii să vorbească despre acelaşi lucru, dar să‑l numească cu cuvinte diferite. Deşi situaţia nu este atît de frecventă, acest tip de falsă dispută consumă de obicei foarte mult timp pentru a fi soluţionată.

Omonimia

O falsă dispută poate apărea atunci cînd preopinenţii dau înţelesuri diferite unui acelaşi termen. Este poate cea mai frecventă sursă de false dispute. (Referitor la disputele dintre filosofi, Bertrand Russel spunea că „La o analiză mai atentă, marea majoritate a problemelor filosofice se dovedesc a fi ori probleme iscate de diferita înţelegere a unor termeni, ori a nu fi deloc probleme filosofice.”) Exemplu: „Masa microscopului meu e mai mare decât masa microscopului tău” – „masa” poate fi înţeleasă ca „măsură a inerţiei” sau ca „porţiunea pe care se aşează lamela cu preparatul”. Dacă A şi B iau cuvîntul în accepţiuni diferite, disputa dintre ei este evident o pierdere de timp.

Erori în argumentare

Transferul falsităţii prin implicaţie

p implică q nu înseamnă că non‑p implică non‑q.

Contra-contra-exemplul

Din nefericire, denumirea de „contra‑exemplu” poate genera uneori confuzii: Faptul că se poate demonstra falsitatea unei propoziţii prin aducerea unui contra‑exemplu naşte ideea că s‑ar putea face şi invers, anume să se susţină valabilitatea propoziţiei printr‑un exemplu opus contra‑exemplului, ceea ce este evident fals. Trebuie înţeles că un contra‑exemplu nu este un exemplu care se opune unui alt exemplu, ci o metodă de a ataca o propoziţie cu pretenţii de universalitate.

Strategii

Într‑o dispută, argumentaţiile preopinenţilor se pot dezvolta în mai multe moduri. Diferitele strategii conduc la următoarea clasificare:

1. Dispută paralel ofensivă. Fiecare preopinent contestă argumentele celuilalt, fără a contra-argumenta. Practic, preopinenţii caută doar să‑şi distrugă reciproc argumentaţiile, fără a construi altceva în loc (Nu mă interesează ce susţii, dar raţionamentul tău e greşit).

2. Dispută paralel defensivă. Fiecare aduce contra-argumente, fără a contesta însă argumentele celuilalt. Cu alte cuvinte, fiecare îşi susţine propriile idei fără a ţine cont de faptul că adversarul susţine idei contrare (Nu mă interesează unde greşeşti, dar ce susţii e fals).

3. Dispută asimetrică. Unul din preopinenţi se rezumă la a contesta sistematic argumentele celuilalt, care, la rîndul lui, nu contestă nimic, ci încearcă să‑şi susţină poziţia prin argumentare multiplă.

4. Dispută degenerativă. Atenţia şi energia preopinenţilor coboară în permanenţă pe ramurile arborelui logic, din sub‑dispută în sub‑dispută, fără ca partenerii să revină vreodată la concluziile a căror negare a generat fiecare sub‑dispută.

5. Dispută echilibrată. Ambii preopinenţi se preocupă în mod echilibrat atît de construirea de contra-argumente care se opun concluziilor adversarului, cît şi de contestarea argumentelor lui.

Tehnici ne-ortodoxe

Unele argumente, chiar dacă respectă o anume logică, pot încerca să introducă în universul discuţiei elemente care nu ţin de ceea ce se discută, ci de persoanele concrete care poartă discuţia. În general, acestea sunt argumente privind competenţa:

1. discreditare

2. apel la autoritate

În discuţiile între parteneri umani nu se poate face abstracţie de factori psihologici, care sunt inerenţi firii umane. Aceşti factori nu apar în arborele logic, dar influenţează modul cum decurge o discuţie. De aceea, chiar dacă nu sunt argumente propriu‑zise, studiul lor este important.

1. insultă

2. intimidare

3. apel la sentimente

4. influenţa „suporterilor”

5. ridiculizare

În fine, ultima categorie de tehnici ne‑ortodoxe (şi cea mai îndepărtată de planul logic) o formează „argumentele” care de fapt n‑au legătură nici cu competenţa persoanelor care poartă discuţia, nici cu resorturile lor psihologice, ci sunt pur şi simplu perturbări violente ale canalelor fizice prin care se realizează comunicarea.

1. întreruperi repetate

2. ridicarea vocii

3. forţa fizică

Trebuie observat că toate aceste tehnici ne‑ortodoxe nu sunt lipsite de fapt de logică (nu sunt comportări iraţionale, aberante), dar motorul logic care le propulsează nu merge în direcţia impunerii ideilor pe plan logic.

Exemple

Acest capitol cuprinde exemple de dispute şi pledoarii din presă, analizate în scopul evidenţierii noţiunilor introduse de modelul discuţiei şi de cel al argumentării, dar mai ales în scopul evidenţierii erorilor, tehnicilor ne-ortodoxe etc.

*** Urmează fragmente din versiuni anterioare ale lucrării. Acestea sunt „bucăţi” nefinisate pe care eventual le voi adapta/modifica/rescrie în vederea includerii lor în capitolele deja scrise sau în cele aflate încă în lucru.

Types of Objection

1. Modus Ponens. Let g be a sentence. The conjunction

(g implies d) and dnot

is an objection by Modus Ponens. Because

(g implies d) is_equivalent_to (dnot implies gnot),

the conjunction can be written

dnot and (dnot implies gnot),

from which, putting dnot = d’, we get

d’ and (d’ implies gnot),

which is exactly an objection to g.

2. Counter‑example. Let "x, P(x) be an universal sentence. A counter‑example is a value x_k for which ¬P(x_k). Practically, a counter‑example proves the sentence $x, ¬P(x), which is nothing else but the negation of the universal sentence.

Counter‑examples occur frequently when an implication between predicates is involved: Let us take the implication "x, P(x) => Q(x); a counter‑example is any particular value x_k for which P(x_k) & ¬Q(x_k) (i. e. the negation of the implication). Among these cases, many follow the scheme: „It’s not true that P(x) implies Q(x), but P(x) implies (Q(x) or R(x)) – here is an example for which, P(x_k) being true, R(x_k) does happen and Q(x_k) does not”.

Definition

I call definition a sentence

n = x <=> C(x),

where C(x) is a predicate of variable x which sets the definition’s conditions, and n is the notation for x. A definition can be read „I put n for x if and only if x complies to the conditions C(x)”, or „Saying ‚x is n’ is equivalent to saying ‚x complies to the conditions C(x)’”, or yet „n means those x that are complying to the conditions C(x)”.

It should be noticed that the known notions of notation and convention are equivalent to the notion of definition, as introduced above. A classification is a multiple definition, in the sense that it defines simultaneously some classes (through their properties), each of them having associated a certain notation (or name).

A definition is always true. The only thing one can doubt is the assumption that it was (or is) used identically by others (or even by the opponent). For example, I am entitled to argue if my opponent says „In Geometry, a set of three segments is called a triangle” (I can put on the table Geometry textbooks), but is absurd to argue if he says „I call triangle a set of three segments”. (What to put on table to prove that „It’s false that you call triangle a set of three segments”? A Psychic?) To object becomes again legitimate if the opponent stated (or implied) previously, during the same dispute, that „I call triangle a set of three points”.

Two definitions that have one element in common (the notation or the conditions) will define terms that are:

synonyms: n = x <=> C(x) vs. n’ = x <=> C(x),

homonyms: n = x <=> C(x) vs. n = x <=> C’(x)

Synonyms are in fact different notations for the same thing, and homonyms are identical terms having different meanings.

Being a process by which someone sustains a certain idea, an argumentation is not a perfect body of logic or an absolute truth. Generally, about none of the arguments can be said they are true or false, unless adding „Until the contrary is proved”. An assertion denied by the opponent remains part of the argumentation until its author rejects it explicitly.

---------------------

Un exemplu complex

Structură ascunsă

Aşa cum s‑a putut observa mai devreme, nu este obligatoriu ca toate elementele argumentului să fie enunţate explicit. Uneori, mai mult chiar decât omiteri, în vorbire au loc substituţii: în locul structurii, se enunţă structura‑p:

„Dacă Dan a zis că şi‑a luat maşină, atunci aşa e!”

Deşi pare că această implicaţie este structura unui argument, totuşi ea, fiind o implicaţie particulară, nu poate susţine un argument. O analiză mai profundă relevă existenţa aici a unui argument cu următoarea structură: „Dacă un om «ca Dan» (un om de cuvânt, care nu aruncă vorbe‑n vânt) a spus că a făcut un lucru, atunci înseamnă că el a făcut într‑adevăr lucrul respectiv” şi cu baza: „Dan este un om «ca Dan» (de cuvânt) şi Dan a spus că şi‑a luat maşină.” Prin omiterea din discurs a condiţiei ca persoana să fie „de cuvânt” (condiţie esenţială, pentru că altfel nu s‑ar putea susţine implicaţia), argumentul pare a avea structura „Dacă X spune că a făcut Y, atunci înseamnă că X a făcut într‑adevăr Y”, care este evident o implicaţie falsă.

Structură multiplă – bază multiplă

Este vorba deci de o ipoteză multiplă, care cere o bază multiplă:

              Structura (cu ipoteză multiplă):     „Dacă (X este om de cuvânt) şi

(X a spus că a făcut Y),

atunci înseamnă că X a făcut într‑adevăr Y.”

                                Structura‑p rezultată:     „Dacă (Dan este om de cuvânt) şi

(Dan a spus că a şi‑a luat o maşină),

atunci Dan şi‑a luat într‑adevăr o maşină.”

                                         Baza (multiplă):     „(Dan este om de cuvânt) şi

(Dan a spus că şi‑a luat maşină).”

                                                Concluzia:     „Dan şi‑a luat maşină.”

Înlănţuirea argumentelor

O implicaţie cu ipoteză multiplă se poate însă descompune în două implicaţii (pentru demonstraţie, a se vedea Anexa):

„I1 şi I2 Þ C”  Û  „I1 Þ (I2 Þ C)”

Cu alte cuvinte, implicaţia cu ipoteză multiplă se mai poate exprima şi ca:

„Dacă X este om de cuvânt, atunci este adevărată următoarea implicaţie: «Dacă X a spus că a făcut Y, atunci înseamnă că X a făcut într‑adevăr Y».”

Aceasta conduce la ideea descompunerii argumentului într‑o înlănţuire de două argumente:

Argument1:

            Structura1:     „Dacă X este om de cuvânt,

atunci are loc implicaţia:

     «Dacă X a spus că a făcut Y,

     atunci X a făcut într‑adevăr Y».”

        Structura‑p1:     „Dacă Dan este om de cuvânt,

atunci are loc implicaţia:

     «Dacă Dan a spus că a făcut Y,

     atunci înseamnă că el a făcut Y».”

                  Baza1:     „Dan este om de cuvânt.”

           Concluzia1:     „Dacă Dan a spus că a făcut Y,

atunci înseamnă că el a făcut Y.”

Argument2:

                 Structura2:     „Dacă Dan a spus că a făcut Y,

atunci înseamnă că el a făcut Y.”

             Structura‑p2:     „Dacă Dan a spus că şi‑a luat maşină,

atunci înseamnă că el şi‑a luat într‑adevăr maşină.”

                       Baza2:     „Dan a spus că şi‑a luat maşină.

                Concluzia2:     „Dan şi‑a luat într‑adevăr maşină.”

Schema acestui mod de susţinere a concluziei finale este:

Implicaţia absolută şi implicaţia relativă

Aşa cum am arătat mai sus, implicaţia „A Þ B” este echivalentă cu exprimarea „Ori de câte ori se întâmplă A, se întâmplă şi B”. „Ori de câte ori” poate însemna „Ori de câte ori am observat eu” sau „Ori de câte ori în mod absolut”. Primul sens face ca implicaţia să fie relativă, al doilea ca ea să fie absolută. Dacă implicaţiile relative este evident cum apar (prin împărtăşirea unui şir de experienţe personale – de exemplu „De câte ori am fost la restaurantul R, au avut mâncare proastă”), problema implicaţiilor absolute este mai delicată. Practic, dacă există măcar o implicaţie absolută, atunci din ea se poate deduce un şir întreg de implicaţii absolute (prin tranzitivitate: A Þ B şi B Þ C conduce la A Þ C etc.). Problema se reduce deci la găsirea măcar a unei implicaţii absolute. Cum datele senzoriale nu ne vor permite niciodată descoperirea unor implicaţii absolute, ele trebuie postulate. Odată postulată, o implicaţie absolută va fi adevărată atâta timp cât observaţiile nu o vor infirma printr-un contra-exemplu.

Spre exemplu, dacă după 20 de jocuri la un jackpot, un jucător observă că de fiecare dată când apare combinaţia măr-măr-cireaşă, ea este urmată de combinaţia câştigătoare BAR-BAR-BAR, atunci el este îndreptăţit să afirme că „măr-măr-cireaşă implică BAR-BAR-BAR”. Această afirmaţie este logic îndreptăţită chiar dacă numărul total de experienţe a fost extrem de redus şi chiar dacă măr-măr-cireaşă a apărut o singură dată[10] (dar a fost urmat de BAR-BAR-BAR). Bineînţeles, dacă se continuă experienţele şi se observă un caz în care măr-măr-cireaşă nu este urmat de BAR-BAR-BAR, atunci implicaţia devine falsă. Acest experiment ipotetic scoate în evidenţă rolul implicaţiei de a exprima nimic mai mult decât că „ori de câte ori are loc A, are loc şi B”.

Revenind la exemplul pe care‑l discutam, mulţimea enunţurilor aflate în discuţie este

E = {e₁, e₂}, unde

e₁ = „Ionescu şi‑a cumpărat o maşină.” şi

e₂ = „Ionescu şi‑a cumpărat o garsonieră.”

Se observă că există unele lucruri comune în enunţurile celor doi. Acestea s‑ar putea formula ca propoziţia

“Ionescu şi‑a cumpărat o ............”,

despre care X susţine că trebuie completată cu „maşină”, iar Y cu „garsonieră”. Numesc elementele fixe concordanţe. Atunci, elementul asupra căruia X şi Y au păreri diferite este o discordanţă (în general, pot exista mai multe discordanţe). Valorile concrete propuse de cei doi pentru a înlocui discordanţa le numesc susţineri.

Mulţimea enunţurilor se poate deci reprezenta cu ajutorul unui predicat de variabilă v şi a mulţimii susţinerilor preopinenţilor:

E = {“Ionescu şi‑a cumpărat o ....v....” | v Î {“maşină”, „garsonieră”}}.

Pentru două discordanţe, mulţimea enunţurilor se exprimă în general ca:

E = {P(v₁, v₂) | (v₁, v₂) Î S},

unde predicatul ar putea fi P(v₁, v₂) = „....v₁.... şi‑a cumpărat o ....v₂....”, iar mulţimea susţinerilor ar putea fi S = {(“Ionescu”, „maşină”), (“Georgescu”, „garsonieră”)}.

Dacă sunt nu doar două, ci d discordanţe, predicatul propoziţional este P(v₁, v₂... v_d). Pentru a reprezenta mai compact setul de d variabile, definesc vectorul de discordanţă v = (v₁, v₂... v_d). Cu această notaţie, predicatul propoziţional se scrie simplu P(v).

Revin acum la cazul particular cu două discordanţe. Mulţimea susţinerilor S este formată din propunerile concrete ale celor doi preopinenţi, adică din seturi asemănătoare variabilei vectoriale v = (v₁, v₂):

c₁ = (“Ionescu”, „maşină”) şi c₂ = (“Georgescu”, „garsonieră”).

Acestea sunt constantele (valorile concrete ale variabilei vectoriale v), care, înlocuite în predicatul P(v), generează enunţurile celor doi preopinenţi:

P(v) = „....v₁.... şi‑a cumpărat o ....v₂....”

P(c₁) = „Ionescu şi‑a cumpărat o maşină.” = e₁

P(c₂ ) = „Georgescu şi‑a cumpărat o garsonieră.” = e₂

În general, dacă nu sunt doi, ci p preopinenţi, atunci mulţimea susţinerilor este alcătuită din cele p constante propuse de ei pentru a înlocui variabila v:

S = {c₁, c₂... c_p}.

Se poate acum scrie mulţimea enunţurilor în cazul general (d discordanţe şi p preopinenţi):

E = {P(v) | v Î S}, cu

v = (v₁, v₂... v_d) şi

S = {c₁, c₂... c_p}, astfel încât

e_i = P(c_i), "i Î {1, 2... p}.

Această formă de reprezentare o numesc forma normală a mulţimii enunţurilor, iar procesul de trecere de la forma iniţială la cea normală îl numesc normalizarea enunţurilor. Acest proces este caracteristic studiului disputei şi (de obicei) nu este realizat în mod conştient de preopinenţi.

Trebuie observat că, atunci când am definit matricea atitudinilor, nu am precizat dacă se foloseşte forma iniţială a enunţurilor, e_i, sau forma normală, P(c_i). Această observaţie conduce la definirea unei condiţii esenţiale: normalizarea enunţurilor nu trebuie să schimbe matricea atitudinilor. Cu alte cuvinte, reformularea enunţurilor în vederea identificării modelului logic comun nu trebuie făcută în aşa fel încât preopinenţii să‑şi schimbe atitudinile faţă de ele. Pentru că altfel, studiul ar altera însuşi obiectul şi de fapt s‑ar ajunge să se studieze alt obiect.

Rolul variabilelor propoziţionale se poate lărgi, cuprinzând şi concordanţele. Pentru aceasta trebuie definit un predicat propoziţional cât mai general, considerând toate elementele posibile ca discordanţe virtuale, rămânând apoi ca elementele care întrunesc efectiv acordul preopinenţilor (concordanţele) să fie identificate abia după ce se face analiza valorilor concrete ale fiecărei variabile. O astfel de abordare, mai generală, îşi dovedeşte valoarea în cazurile în care preopinenţii ajung la concluzia că ceea ce considerau la început o concordanţă era de fapt o discordanţă. Reluând exemplul în care unica discordanţă era maşină/garsonieră, X şi Y ar trebui să înceapă prin a se întreba:

„Sigur vorbim despre aceeaşi persoană?”

„Sigur vorbim despre o achiziţie, şi nu despre o închiriere, moştenire, furt etc.?”

„Sigur vorbim despre o acţiune trecută, şi nu cumva despre una viitoare?” şi aşa mai departe. Dacă răspunsul la vreuna din aceste întrebări este „nu”, atunci precizarea discordanţei are mari şanse să ducă automat la soluţionarea disputei. Recunoaşterea discordanţelor „mascate” devine însă dificilă dacă ele se află printre elementele nemanifestate explicit, pe care preopinenţii le consideră subînţelese. De exemplu, X ar putea subînţelege că „Ionescu şi‑a cumpărat o maşină ieri”, iar Y că „Ionescu şi‑a cumpărat o garsonieră acum trei luni.” Aceste elemente suplimentare, care pot ieşi la iveală pe parcursul disputei, le numesc circumstanţe. Ele sunt răspunzătoare de eventuala modificare a predicatului propoziţional şi de creşterea numărului de variabile în timpul disputei.

---

[1] Scopul introducerii acestei ordini este strict limitat la uşurinţa reprezentării grafice şi nu atribuie ‚incertului’ o valoare de adevăr intermediară, situată între ‚fals’ şi ‚adevărat’.

[2] De fapt, tranziţie înseamnă afişarea (prin mijloace verbale sau non-verbale) a unei alte păreri.

[3] Spaţiul enunţurilor este unul singur şi se îmbogăţeşte în timp cu noi elemente; spaţii ale atitudinilor sunt mai multe – fiecare enunţ generează câte un „mini-”spaţiu de atitudini propriu.

[4] În exemplul studiat, subiectul disputei este ?„Ionescu şi-a cumpărat o maşină”.

[5] Un exemplu de eşec al avocatului: Înaintea alegerilor, X este nehotărât – „Să votez cu partidul Y? Să nu votez cu ei?...”; după ce Y îşi susţine platforma program, X decide „Da, m-am hotărât: Nu votez cu Y.”

[6] Spre exemplu, doi indivizi pot avea o dispută pe tema existenţei zeilor. Dacă la un moment dat începe un cutremur, cel care susţinea că zeii nu există ar putea ieşi în fugă, ţipând „Da, acum cred! Zeii există! Şi iată, mă pedepsesc pentru necredinţa mea!”. Evident, schimbarea părerii lui nu a fost provocată de vreun argument al preopinentului.

[7] Prin „limbaj” înţeleg limbă (vorbită sau scrisă).

[8] Implicaţia mai poate fi derivată (prin logică) din alte implicaţii, caz în care implicaţiile-sursă au rol de simple consemnări ale unor observaţii; dacă şi (unele din) acestea sunt deduse, atunci se coboară pe arborele de inferenţe.

[9] Exemplu: „De ce partea zecimală a unui logaritm se numeşte mantisă?”

[10] La limită, implicaţia este valabilă chiar dacă măr-măr-cireaşă nu a apărut nici măcar o dată (falsul implică orice).