Building an Universe

by Vlad Enache

1. Purpose

The purpose of this paper is to establish some general guidelines for building a system complex enough that self‑reproductive subsystems (SRS) could emerge and evolve in it. We will call this system “Universe”. By “building” a Universe we mean modeling it (i.e., at least specifying its components, their properties and the functional relationships between them, and maybe implementing this model on a computer), not necessarily building it physically.

From the guidelines so established, we will deduce some general properties of such a Universe.

2. Requirements

The acceptable means by which the Universe has to be built are purely logical – this means that any logically self‑consistent (non‑contradictory) structure can be used. However, we choose to impose two additional restrictions, one of which was already mentioned:

1. The Complexity Principle: The Universe has to be complex enough so that SRS (self‑aware subsystems) could appear spontaneously and evolve in it.

2. The Economy Principle: The informational effort for building the Universe should be minimum.

In other words, we should achieve maximum complexity with minimum effort.

Of course, the choice of grounding the whole building into these two requirements is subjective. This paper does not aim at justifying this choice, but at deriving the consequences of the two principles above, once they are accepted.

3. Things to avoid

The Universe we are trying to build should not be inspired by the world we live in. We have to restrain ourselves from copying the Physics of our real world. The aim is not to build a plausible theory/explanation of our world. Whenever a new idea is to be evaluated, arguments like “Let’s drop this idea, because this is not how things work in our world” should be disregarded (as well as “Let’s embrace this idea, because this is how things do work in our world”).

If it happens that certain things we build work similarly to real things in our world, this should be regarded as a coincidence – a remarkable, maybe astonishing fact, but nevertheless a coincidence. The path we take should be permanently isolated from any temptations of modeling the real world. If, at the end of this journey, we will find some interesting coincidences, we need to be sure they came up based purely on the two principles stated above. Otherwise, the generality and the value of our findings will be greatly reduced[1].

If we establish clearly that certain things/behaviors/laws derive logically from the two fundamental principles only, and they are similar to some real things/behaviors/laws, then we will name them using the same word as in the real world. But we will spell the word using Greek letters, to remind us that it is not “the real thing”, but something just accidentally very similar to it.

4. The building blocks

The Universe is a system. For describing it, we need to specify three things:

a) how it is built

b) how it works

c) its initial state.

For now, let’s concentrate on steps a) and b). According to The Complexity Principle, these steps should allow enough complexity so that SRS are possible. But The Economy Principle requires that these steps involve as little informational effort as possible. The simplest idea is to break up the big system into many smaller identical sub‑systems. This way, the overall complexity remains high, while the total building effort is dramatically reduced – we need to describe only one sub‑system, then issue a “repeat N times” command, then describe the interaction between sub‑systems. As it is known, having N identical sub‑systems interacting generally gives birth to more complexity than N times the complexity of each sub‑system[2]. This way, we can economically increase the total complexity by simply increasing N.

So, the first consequence of our two basic principles is: the Universe has to be built out of many identical interacting sub‑systems. We will call these sub‑systems cells (cells). “Many” could very well mean “infinite”, but since this would make our Universe too big for practical purposes (i.e., a computer simulation), we will consider that N is finite.

5. The anatomy of a cell

A single cell is a system. For describing it, we need to specify three things:

a) how it is built

b) how it works

c) its initial state.

Again, let’s postpone the initialization problem and focus on a) and b). In general, a system is described by a set of parameters. The number of parameters can be infinite, but for practical purposes we will consider n parameters. Each parameter can take values in a certain range, which can be a finite or an infinite set. For the sake of simplicity (and The Economy Principle), we will consider that each range is not only finite, but is reduced to the minimum: the set {0,1}.

Since these parameters completely describe the cell, we need not dig deeper – we can say that the cell actually is a zero‑based array of n binary parameters: (p₀, p₁, p₂, ..., p_n‑1). Such an array we will call the state C of a cell. When talking about unspecified parameters, we will use lowercase letters: k, a, x, y, z etc. (each of them could be p₀, p₁, p₂, ..., p_n‑1).

6. Elementary events

Now that the “how it is built” problem is solved for a cell, let us analyze “how it works”. “To work” means “to change”, and the only thing to change is the state of the cell. The minimum possible change (“atomary change”, so to speak) is changing the value of only one parameter. Let this parameter be p_k. What should we consider as an elementary change? Let us consider all possible combinations for old and new values of p_k. There are four possibilities:

old	new		old	new		old	new		old	new
0	0		0	1		0	0		0	1
1	0		1	1		1	1		1	0
reset			set			no change			flip

The first two tables show the new value not dependending on the old one – they are the “reset” and “set” actions. Then, there is one “no change” action, which of course we don’t need. Finally, there is a “flip” action, which changes 0 in 1 and vice versa.

“Set” and “reset” define a pair of elementary changes: one is useless without the other (e.g., if we admit only “reset” changes, then all the parameters will eventually become 0 and the system will “freeze”). For each action we would have to identify which of the two changes has to be performed – set or reset? This means additional information, additional effort. We would like one elementary change, not two.

But there is an even more serious disadvantage of “set” and “reset”: they cannot be applied repeatedly. If we try to, the effect is lost – the value of p_k cannot be set (or reset) two or more times in a row (actually it could, but it would lead to no further change).

The last table, “flip”, is free of all these problems: it is one elementary change that can be applied repeatedly without worry, because it does not destroy information about the old values. So this will be our choice of elementary event: “flip the value of p_k”.

Let us define the “flip k” operator, which applied to a state C of a cell transforms it into a new state C’ so that all parameters keep the same values, except p_k, which gets flipped. The “flip k” operator will be written as (k):

(k)C = C’

If we need to flip two parameters we will write (k₁)(k₂)C. Any change of state, no matter how complex, can be expressed as an array of flip operators. There are some obvious properties these operators have:

(k)(k) = 1  –  “1” is the unity operator, which leaves the state unchanged

(k)^‑1 = (k)  –  any flip is it’s own inverse

(k₁)(k₂) = (k₂)(k₁)  – the flip operators commute.

One interesting thing to note is that flipping the value of p_k can be written using the “xor”[3] logical operator, which we will write “+”: p_k’ = p_k + 1. This operation can also be regarded as modulo 2 addition.

7. Chemistry (Chemistry)

With the anatomy of a cell being defined and having also some elementary events at hand, we can start thinking of a set of rules governing how an isolated cell changes its state. These “internal laws” we will call Chemistry (Chemistry). All the laws will share a common pattern: they will tell how a parameter changes according to some condition.

But the flip operators are unconditional – they apply blindly to any state. This cannot create much complexity. We need the flip operators to be triggered by some conditions. The only variable things in a cell are the values of its parameters, so the conditions must refer to these values. The simplest test is to check the value of one parameter. This way, we introduce the “conditional flip” operator: (k|a) means “p_k gets flipped iff p_a = 1; otherwise, p_k remains unchanged”. Of course, the negated condition is (k|¯a), meaning “p_k gets flipped iff p_a = 0; otherwise, p_k remains unchanged”. The conditional flip operators have these properties:

(k|a)(k|a) = 1

(k|a)^‑1 = (k|a)

(k|a)(k|~a) = (k)

(k|~a) = (k|a)(k)

(k)(k|a) = (k|a)(k).

Unfortunately, conditional flip operators generally do not commute. Operators (k₁|a₁) and (k₂|a₂) commute in a particular case only: if  k₁ ≠ a₂ and k₂ ≠ a₁. This means that k₁ and k₂ must belong to a “k only” subset of parameters, while a₁ and a₂ belong to an “a only” subset. These two subsets must be disjoint. So if we want to work with commutable operators, we need to define two disjoint subsets of parameters, K and A, and have all our conditions in A and all the flips in K. Since parameters in A will never change (all flips occur in K), the evolution would not be so interesting.

The solution is to redefine the composition of two operators. Let us take (k₁|a₁) (k₂|a₂)C. Instead of saying that it means (k₁|a₁) applied to (k₂|a₂)C, we will say that (k₁|a₁)(k₂|a₂) is a new operator which gets applied to C “in one shot”: we check a₁ and a₂ in C, then decide all the flips, then apply them to C. This way, one operator cannot influence other operator’s condition, so they can commute freely.

If we have more operators trying to flip the same parameter, we can even aggregate their conditions: (k|a₁)(k|a₂)(k|a₃) can be written as (k|a₁,a₂,a₃), meaning “p_k gets flipped once for each p_a1 = 1, p_a2 = 1, p_a2 = 1 condition that is met”. This can be written[4]:

p_k’ = p_k + p_a1 + p_a2 + p_a3.

Of course, if some of the conditions are negative we write their corresponding terms negated.

If the condition list is empty, we rediscover the unconditional flip operator (k). This works as if it is conditioned by a “virtual parameter” which is always 1: p_k’ = p_k + 1. So (k) could be written (k|1). Similarly, the unity operator (which leaves any state unchanged) could be written (k|0).

But the unity operator needs not a specific k, so let us introduce “*” as a sign for “any k”. The unity operator becomes (*|0). Similarly, (*|1) means “flip all the parameters”, so (*|1)C = ~C. This means (*|1) does the same thing as the negation operator applied to a state.

Generally, a Chemistry law will be written as a simple conditional flip: (k|a). For a certain parameter p_k, if there are more Chemistry laws telling it to flip, we can aggregate all the conditions as shown before: (k|a₁,a₂,...,a_q,~b₁,~b₂,...,~b_s). The next value of p_k will be:

p_k’ = p_k + (p_a1 + p_a2 + ... + p_aq) + (~p_b1 + ~p_b2 + ... + ~p_bs)

This can be written as:

p_k’ = p_k + _S (a_ki ∙ p_i) + _S (b_ki ∙ ~p_i),

where coefficients a_ki and b_ki are either 1 or 0, depending on the presence/absence of parameter p_i in the list of conditions for flipping p_k. This way we can use matrices to write the transform for the whole state:

Or, making some useful notations:

C’ = C + A∙C + B∙(~C)

But let us remember that ~p_i = p_i + 1, so we can express ~C as:

Writing 1 for the unity vector, we have:

C’ = C + A∙C + B∙(C + 1)

The first term, C, can be written as I∙C (where I is the standard unity square matrix), so:

C’ = I∙C + A∙C + B∙C + B∙1

C’ = (I + A + B)∙C + B∙1

C’ = M∙C + R,

where M is a square matrix and R is a vector (both containing only 0 and 1).

This is a rather simple transform: C gets multiplied by a constant matrix M, then a constant vector R is added.

M and R define the standard form of Chemistry laws: for parameter p_k, the standard conditional flip is (k|m₁,m₂,...,m_t,r), where none of m₁, m₂, ... m_t is negated and r is either 1 or 0 (in case it is 0, it may be skipped). It is easy to show that any complex conditional flip can be brought to this standard form.

While the vector R can be arbitrarily chosen, the matrix M has to obey one condition: it should not be singular. Indeed, if M is singular, it follows that there are vectors K so that the equation M∙C = K has no solution for C. Then, C’ = K + R is a state which cannot be obtained, no matter how we choose C:

C’ = K + R = M∙C + R (which C satisfy this?)

K = M∙C (no solution for C).

Such C’ = K + R states are useless, since they are forbidden forever. This would be a waste of resources (and, most importantly, a waste of building effort), so if we want to follow The Economy Principle we have to rule out such situations. This is why matrix M should be non-singular, thus invertible.

One important consequence is that there are no two different states C₁ and C₂ leading through Chemistry to the same C’. Indeed, let us suppose:

M∙C₁ + R = M∙C₂ + R

M∙C₁ = M∙C₂

M∙(C₁ + C₂) = 0

But because M is non-singular, M∙X = 0 has the only solution X = 0. This means:

(C₁ + C₂) = 0

C₁ = C₂

The Chemistry can be regarded as a function:

C’ = c(C), where c(X) = M∙X + R

The domain and co-domain of c are the same: the space C of all possible cell states. C is finite.

Also, we showed earlier that c is surjective (all states C’ can be reached) and injective (different C states lead to different C’ states), so c is a bijection.

A bijection from a finite set C to itself is nothing else but a permutation of its elements. C having 2ⁿ elements, there are 2ⁿ! possible permutations. Not all of these permutations are represented by functions c defined in terms of M and R, as above.

An important remark: For any permutation there exists an integer t such that applying the permutation t times, we get the initial thing.

For our function c, we can write:

($) t Î N such that (") X Î C, c^t(X) = X.

This means any function c gives birth to a cycle (of some length t): if we start with an arbitrary X and apply t times c, it is guaranteed we will return to X.

But for a specific X, the cycle needs not be exactly t. It can be shorter (some divisor of t). Let us write t(X) for the length of the cycle started by X:

(") X Î C, ($) t(X) Î N such that c^t(X)(X) = X.

Generally, t is the smallest common multiple of all t(X).

Furthermore, matrix M alone is a particular case of function c (having R = 0), so it represents a permutation, so there exists a power k such that M^k = I.

... <more work to be done here> ...

Having the state of each cell packed in its state vector, let us build a tall vector U representing the state of the Universe. The Chemistry for the whole Universe can be written:

,

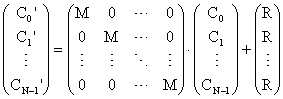where M is the square matrix defined earlier, R is a vector and C are also vectors (states of the cells). Note that the elements of the vectors and of the square N × N matrix above are themselves vectors/matrices.

The zero entries in the diagonal matrix above are square n × n null matrices (same size as M, but filled with zeroes). These matrices are null because Chemistry talks only about how a cell’s new state is influenced by it’s own old state, disregarding the states of other cells – and this corresponds to the main diagonal. What is outside the main diagonal is not Chemistry’s business. It is the domain of interaction between different cells.

The square matrix having matrices as elements can be written as a tensor product:

,

so we can write:

U’ = (I Ä M)∙U + R.

8. Interaction

If we want interaction between cells, then we need to put non-zero matrices outside the main diagonal of the big matrix defined in the previous chapter. Arbitrary matrices would require a lot of information, so we will use the already defined matrix M – actually, to make things more interesting, we will use combinations of powers of M. Here is an example:

This example can also be written in a simpler form using the tensor product:

U’ = (I Ä M + P₂ Ä M² + P₃ Ä M³ + P₄ Ä M⁴ + P₅ Ä M⁵)∙U + R,

where matrices P₂, P₃, P₄ and P₅ are:

.

Note that I in the first term I Ä M can be regarded as P₁ = I.

In general, we can define interaction using a polynomial:

U’ = (P_k-1 Ä M^k-1 + ... + P₂ Ä M² + P₁ Ä M¹ + P₀ Ä M⁰)∙U + R,

where coefficients P_i are N × N matrices with elements 0 and 1 and k is the smallest positive power such that M^k = I.

The only restrictions until now are that P₁ = I and all other P_i have zeroes along their main diagonals.

One common sense restriction would be to have the big matrix invariant to cell permutations. This means the laws of our Universe should be homogenous (the same viewed from any cell). Why? Because building a non-homogenous Universe requires additional information compared to building a homogenous one.

 

 

 

... <leftovers> ...

 

For cells to interact, there are two choices:

a) global interaction: there is one big interaction (involving all the cells), which can be described only globally,

b) local interaction: there is one small interaction pattern that gets repeated over the whole “population”; this smaller interaction involves only several cells and does not depend on cells in the rest of the Universe.

It is arguable which choice serves better our purpose (i.e., the two principles: more complexity with less effort). Saving the debate for later, we will explore here choice b).

Before asking “How does the interaction work?”, choice b) leads to a preliminary question: if not all cells interact all the time, then exactly which cells interact each time? The smaller interaction pattern we need to define involves only several cells – how do we decide which are they in each particular case?

We will call the answer to this question Space (Space). The answer to the other question (“How does the interaction work?”) will be called Physics (Physics). These two are closely related (together, they describe the interaction between cells), but we will deal with them separately.

9. Space (Space)

The minimum number of cells needed for an interaction is two. Faithful to The Economy Principle, let us stick to this minimum and try to define the interaction pattern for two cells. We will call these two cells neighbors (neighbors).

So, the Physics will say “Two neighbors interact in the following way: ...” The job of Space is to choose[5] in some way the two neighbors for each interaction.

Choosing pairs of elements from a set is termed a relation – in our case, the neighborhood relation. It can be conceived as a subset of the set of all cell pairs.

One problem is: specifying such a set requires an enourmous amount of information. No matter how we try to do it, the answer to the question “Which?” requires some labeling scheme, so that we can distinguish between different cells. This labeling scheme grows with the number of cells, so Space depends somehow on how many cells are there in the Universe. Moreover, it has to be integrated also into Physics, so that Physics could understand it (afterall, Physics is the final “beneficiary” of this information). But this defeats the whole purpose of chosing b) over a) (i.e., local versus global).

Let us postpone for now the discussion about the amount of information and focus on the neighborhood relation. Clearly, we don’t need this relation to be reflexive, since the interaction of a cell with itself is already described by Chemistry. So we take neighborhood to be anti-relfexive: no cell is its own neighbor.

Symmetry (if A is neighbor of B, then B is neighbor of A) halves the effort of defining the relation, so we take it to be symmetric.

... <transitivity: needs further discussion> ...

10. Geometry (Geometry)

The neighborhood relation can be either constant or variable in time. If it is constant, it means it is “hard wired” and cannot change – the whole setup effort is concentrated in the beginning, when we set up the neighborhoods (and the effort is pretty big, as we showed). This choice clearly violates The Economy Principle.

On the other hand, a variable neighborhood not only lessens the initial effort, but also creates more complexity. So this will be our choice: variable neighbors. There is yet another advantage, related to the labeling scheme problem left unanswered above: in a variable neighborhood scheme, what we need is to identify not neighbors, but changes in neighbors. This task is much easier, because we can use a relative labeling scheme: when we need to find out the new neighbors of a cell, we can describe them as related somehow to the old ones. This method assumes there is a given relation between cells: for instance, if we have a total order relation on cells, then we could say “the new neighbor of this cell is 5 cells ahead from its old neighbor”.

But why consider another relation, when we already have one – the neighborhood relation? Using it would be a simpler choice, since it would not involve any additional construct. This means we can describe future neighbors of a cell in terms of “neighbors of its old neighbors”.

The answer to the question “What are the allowed changes of neighbors?” we will call Geometry (Geometry).

Geometry gives structure to Space in time. It is the mechanics of changing neighbors. Actually, it is more like kynematics, in the sense that it describes possible neighbor changes, without taking into account physical reasons. From “Any change is possible”, Geometry rules out some cases, leaving us with “Only these changes are possible”. Then, Physics tells us for each case: “From the range of possible changes, given the specific situation here, this particular change will take place”.

11. Physics (Physics)