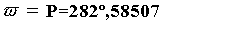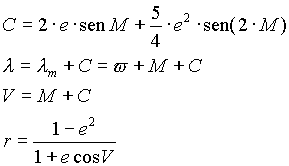Cálculo de la longitud solar

La Tierra describe una órbita elíptica de excentricidad e=0,016718 alrededor del Sol. Nosotros supondremos por la relatividad del movimiento que es el Sol el que lo hace.
Como la excentricidad es pequeña se puede suponer que el movimiento es uniforme y con movimiento medio n=360/365.2422=0,9856 º/día=1,72019E-2rad/día.
Ahora hay que elegir un origen de tiempo por ejemplo época 6.5 Mayo de 1979 con fecha juliana T0==2444000.5. Para este instante la Anomalía Media o ángulo que forma con el perihelio un Sol ficticio que se moviese uniformemente M0=2,12344rad=121º,66415. Para cualquier otro instante t la Anomalía Media vale M=M0+n*t. [amedia.gif]

Pero el Sol describe una órbita elíptica. la longitud a la que ocurre la mínima distancia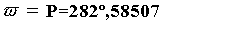
para la época T0. Varía con el transcurso del tiempo lentamente, y en 100 días VP=8.22E-5 radianes, por lo que en la época J2 podemos calcularlo P=P+(J2-T0)*VP/100
La longitud media del Sol vale:

Ahora corrijamos el efecto de que el movimiento no es uniforme, sino que sigue la ley de las áreas. A esta corrección se llama ecuación de Centro y en segundo orden vale:

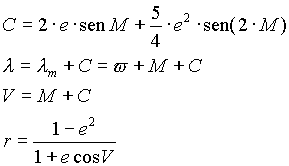donde V es la anomalía Verdadera y r la distancia al Sol en U.A.
Ejemplo: Calcular la longitud solar para el 13 de marzo de 1960 a las 8h 30m TU
1) Calcular la fecha juliana DJ=2437006,85
2) Calcular la Anomalía Media M=M0+n*t = -6771,27729
2a) Conviértelo al primer giro: Como M/360=-18,80910358 sumaremos 19x360º y resulta M=68º,72271.
3)Puedes usar la función parte entera E(x) para calcular M y luego C y la longitud solar

4)Para calcular la Ascensión recta y Declinación basta con convertir de Eclípticas a Ecuatoriales
DC=asin(sin(OB)*sin(L))
AR=acos(cos(L)/cos(DC))
Donde la ambigüedad en la AR se resuelve si L>PI calculando AR=2*PI-AR.
OB es la Oblicuidad de la Eclíptica que vale:
OB=23.452294-(0.46845*Z+0.00000059*Z*Z)/3600 donde Z=(J2-2415020.5)/365.2422
Para el caso que nos ocupa: AR=23h 33m 35s y DC=-2º51'19"