An Example of "Percentage Abuse"
(Ripped from FM radio airwaves!)

If you are hearing nothing, first make sure your speakers/headphones and sound system are on. Next thing to check on is your firewall. If you’re browsing this page with Internet Explorer and you see a band near the top saying “To help protect…” then click the band and select “Allow Blocked Content.” This sound file is in ".mp3" format and is set to play through your browser's QuickTime plug in (Windows Media Player plug-in will do). Here are some other options you can try:
1. Try clicking the boombox, especially the area below it (between the boombox and "Technical difficulties?").
2. If you're using Internet Explorer, try Netscape instead, or vice-versa.
3. Go to http://www.apple.com/quicktime/download and get the free QuickTime player complete with plug-in.
4. Click http://www.oocities.org/xstatprof/abuse/ad.mp3, download the audio file and use any MP3 player.
5. Right click the link in 4 (above), and save its target (namely, ad.mp3) to your computer's hard drive.
6. Just trust me, it's an actual advertisement claiming: The Club® reduces your odds of car theft by 400%!
The meaning of the word percent can be understood easily by
considering each of it's two syllables. The prefix per
means divided
by, as it often does in Mathematics. It can also mean divided
amoung
or even into, as in dividing the whole into parts. The
suffix cent
refers to 100 as in century (100 years) or centipede (100
legs).
So, percent means divided by 100. That is, the
whole is
divided into 100 parts, all the same size.
No, not really, because all of an entire quantity is 100% of it. So if there is a 100% reduction, then there is nothing left! But what if the 400% is of something else, other than the quantity itself? The really crucial question is:
400% of WHAT?
In order to interpret a percentage, one must first know the answer
to the
question: Percent of what? That is, what is the basis for
the
percentage. Normally this would be the original amount, the
amount that
comes first in time or the amount before some special situation is
considered. So it is natural for us to think that the basis for
percent
in this example should be the likelyhood of a car being stolen when it
is
parked withOUT the Club. But this would make the commercial's
400%
reduction impossible (unless car thieves are giving cars away to people
who use
the Club, ha ha ha). So they must have some other basis in
mind.
What other basis is there? The author(s) of this commercial
apparently
decided to use as their basis the likelyhood of a car being stolen when
it is
parked WITH the Club. This constitutes percent abuse, because it
is not
the natural basis and it produces a result that is misleadingly
large. In
fact, it's rediculously large, enough to cause an educated person to
question
the motives and value system of anyone whose ethics would allow them to
commit
this kind of Statistical abuse.
|
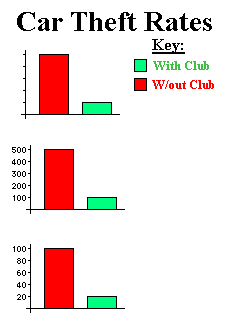
Suppose the data used in this example actually did show that it is five times as likely for a car without the Club to be stolen when compared to a car using the club, as illustrated by the top graph to the right. |
|
|
Numbering the vertical scale using the wrong basis shows how the comercial author(s) could come up with their 400% reduction, as illustrated by the middle graph. |
|
|
Numbering the vertical scale using the natural basis shows how we can come up with the true reduction, as illustrated by the bottom graph. So the true reduction is: 100% - 20% = 80% |
We can easily convert any percent from the wrong basis (i.e. the "after" basis) to the correct basis (i.e. the "before" basis) by using a formula. In the following formula, P1 represents the correct percent using the before basis, and P2 represents the abusive percent using the after basis.
P1 = P2 / (P2 + 100%) * 100%
In our example of a 400% reduction,
P1
= 400% / 500% * 100%
= 0.8 * 100% = 80%
Should we memorize a formula for the rest of our lives? No! Is there something to learn from this? Oh, yes! Be very cautious about buying any product or service that uses statistically abusive advertising. The government can't protect us from those who would use the wrong basis for percentages, but we can infer that those who use such tactics have dubious intent. So, for example, when AOL advertises that... "Spyware can slow browsing by up to 500%," it may mean that they are trying to scare consumers into using their service, or that they are trying to capture the market of those people who are so uneducated that they don't even know this is percent abuse, or...