[Problems]
When the great number scholar gauss of the
world was ten years old, I solved all the
- - problems for 1 for an integer to 100
as follows.
1+2+3 + ... ... +98+99+100
100+99+98 + .. .. .. +3+2+1
Respective - - for the integer of the step
of the top and the step of the bottom 101+101+101
+ .. .. .. +101+101+101 The - of - . 101
measures
100 101X100=10100
This especially consists an integer
to 100
of 1 adding - - - twice 10100/2
= 5,050
Then an answer reaches 5,050.
Answer using this way of thinking in the
anteroom - . (1) * be the integer that it
is for 1 in 200 and it is rub all adding
Sai for the multiple of 3. (2) The unity
of an integer from 1 to x reached 325. Demand
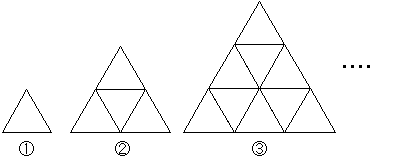
x. (3) One side will heap up the equilateral
triangle of Ko of 1 cm variously bottom diagram
and it will make an equilateral triangle
that is big - - - - . Are several small equilateral
triangles used so that a length of one side
may make 30 cm of equilateral triangles?
01 S School
|