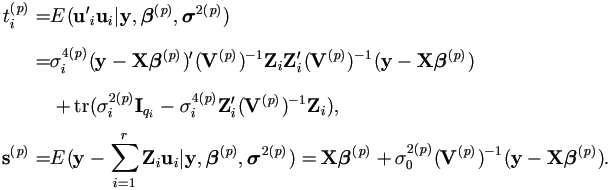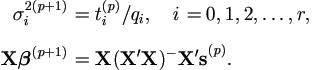Chapter 2 The EM Algorithm
This chapter reviews the EM algorithm in the framework defined by
Dempster et al. (1977). Its application to the
mixed model for complete data is detailed in §2.2. The Monte Carlo EM algorithm (MCEM) is also introduced for implementation purpose.
Assume there are two sampling spaces  and
and  and a many-to-one mapping x
and a many-to-one mapping x  y(x) from
y(x) from 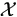 to
to 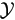 . The observed data y are a realization from
. The observed data y are a realization from 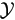 . The corresponding complete data x in
. The corresponding complete data x in 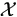 is not observed directly, but lies in
is not observed directly, but lies in 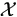 (y), the subset of
(y), the subset of 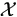 determined by the mapping.
determined by the mapping.
Postulate a family of sampling densities ƒ(x| ) depending on parameters
) depending on parameters 
 Ω, and derive its corresponding family of sampling densities g(y|
Ω, and derive its corresponding family of sampling densities g(y| ) by
) by
 | (2.1) |
The EM algorithm is directed at finding a value of  which maximize g(y|
which maximize g(y| ) given an observed
y, but it does so by making essential use of the associated
family ƒ(x|
) given an observed
y, but it does so by making essential use of the associated
family ƒ(x| ).
).
Definition 2.1
Define the conditional expectation of log ƒ(x| ) given y and
) given y and  0 as
0 as
Q ( | |  0) =
E (log ƒ(x| 0) =
E (log ƒ(x| ) | y, ) | y,  0), 0),
| (2.2) |
where we assume to exist for all pairs
( ,
, 0). In particular assume that
ƒ(x|
0). In particular assume that
ƒ(x| ) > 0 almost everywhere in
) > 0 almost everywhere in
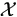 for all
for all 
 Ω.
Ω.
Suppose that  (p) denotes the current value of
(p) denotes the current value of  after p cycles of the algorithm.
after p cycles of the algorithm.
Definition 2.2
Define the general EM iteration  (p) →
(p) →  (p+1) as follows:
(p+1) as follows:
| E-step: | Compute Q ( | |  (p)) for all (p)) for all   Ω. Ω. |
| M-step: | Choose  (p+1) to be a value of (p+1) to be a value of
  Ω which maximizes
Q ( Ω which maximizes
Q ( | |  (p)). (p)). |
| Repeat above iterations until it converges. | |
Let k(x|y,  ) denote the conditional density of x given y and
) denote the conditional density of x given y and  . Based on (2.1), the joint distribution of y and x given
. Based on (2.1), the joint distribution of y and x given  is ƒ(x|
is ƒ(x| ) if x
) if x 
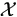 (y), and 0 otherwise. Thus the conditional density of x given y and
(y), and 0 otherwise. Thus the conditional density of x given y and  is simply
is simply
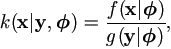 | (2.3) |
and then Q ( |
|  0) =
E (log ƒ(x|
0) =
E (log ƒ(x| ) | y,
) | y,  0) is
0) is
 | (2.4) |
The EM Algorithm for Exponential Families
A simpler form of the EM algorithm is available for the exponential
family, especially for regular exponential family distributions, where
Ω is an r-dimensional convex set such that ƒ(x| ) defines a density for all
) defines a density for all 
 Ω.
Ω.
Suppose that ƒ(x| ) has the exponential-family form
) has the exponential-family form
ƒ(x| ) =
b(x) exp( ) =
b(x) exp( ' t(x)) /a( ' t(x)) /a( ), ),
| (2.5) |
where  denotes a vector parameter and
t(x) denotes a vector of sufficient statistics.
denotes a vector parameter and
t(x) denotes a vector of sufficient statistics.
Theorem 2.1
The EM algorithm for regular exponential family distributions at the iteration  (p)→
(p)→ (p+1) is defined as follows:
(p+1) is defined as follows:
| E-step: | Estimate the complete-data sufficient statistics t(x) by t(p) = E(t(x) | y, (p)). (p)).
|
| M-step: | Determine  (p+1) as the solution of equation
E(t(x) | (p+1) as the solution of equation
E(t(x) |  ) = t(p). ) = t(p).
|
This is due to  , and the Sundberg's formulae (Sundberg, 1974) for regular exponential-family,
, and the Sundberg's formulae (Sundberg, 1974) for regular exponential-family,
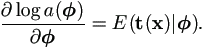
2.2 Mixed Models with Complete Data
This section details the EM algorithm for mixed models with data from multivariate normal distribution, and assume no censoring is present. More details can be found in Searle et al. (1992) and others.
2.2.1 Model and Observed Likelihood Function
The n×1 vector of observations y is taken to have model equation
| y = Xβ + Zu + e. | (2.6) |
The fixed effects on y are represented by β, and the random effects by u, with
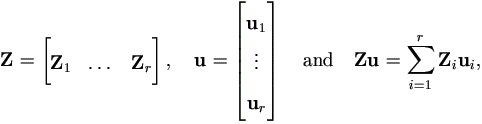
where ui is the qi × 1 vector of the effects for
all qi levels of a random factor i occurring in the data, and Zi is the corresponding n × qi design matrix. Let q =  qi, then u is a q × 1 vector for all random factors and design matrix Z is of n × q. A notational convenience is to define u0= e, q0= n, and Z0= In. This gives the model as
qi, then u is a q × 1 vector for all random factors and design matrix Z is of n × q. A notational convenience is to define u0= e, q0= n, and Z0= In. This gives the model as
y = Xβ
+ 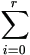 Zi
ui. Zi
ui. | (2.7) |
As usual assume for all i and j (0 ≤ i ≠ j ≤ r),
E(ui) = 0,
var(ui) = σi² and
cov(ui, uj) = 0.
and
cov(ui, uj) = 0.
In particular, denote σ0² by σe²,
E(e) = 0, var(e) = σe² In and cov(ui, e) = 0.
Using these assumptions in the model (2.6) leads to
E(y) = Xβ and
V = var(y) = 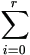 ZiZ'iσi².
ZiZ'iσi².
Furthermore, if y ~ Nn(Xβ, V), the likelihood function is
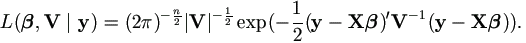
2.2.2 Complete Data Likelihood Function
The key to applying EM algorithm here is to think of the unobservable random effects ui as a part of the data, which are missing though. Then treat the complete data as being y augmented by unobservable random effects u, and the incomplete data as being the observed data y itself only. Under normality of y and u, the joint distribution of y and u is also multivariate normal N(μ, Σ), where
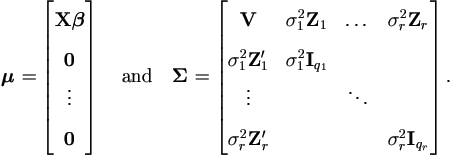
This gives the joint density function as

It is easy to show that  by the Schur formulae. Also since
by the Schur formulae. Also since
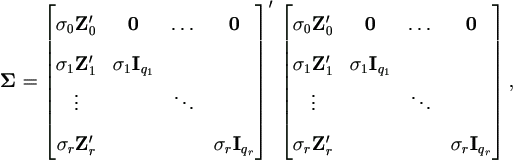
the formulae for the inverse of such matrix (see Searle et al. (1992), p.450) gives

Hence the log-likelihood based on the complete data, y, u1, u2, ..., ur, is

Note u0 = e = y - Xβ
-  Ziui.
Ziui.
Therefore the maximum likelihood estimators based on the complete data are

2.2.3 EM Algorithm Formulation
The complete data sufficient statistics are u'iui
and y -  Ziui.
To apply the EM algorithm, we need their conditional expectations given y. By multivariate normal
theory, the conditional distributions of ui given y for i = 1, 2, ..., r are
Ziui.
To apply the EM algorithm, we need their conditional expectations given y. By multivariate normal
theory, the conditional distributions of ui given y for i = 1, 2, ..., r are
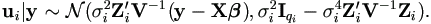

Since E(u'iui|y) = E(u'i|y)E(ui|y) + tr(var(ui|y)), then

and since V = 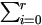 ZiZ'iσi², then
ZiZ'iσi², then
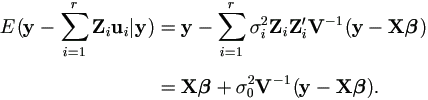
Therefore the EM algorithm for complete data is as follows.
| Step 0. | Decide on starting values for parameters β (0) and σ2(0). Set p = 0. |
| Step 1. | (E-step). Estimate the conditional expectations of complete data sufficient
statistics. Let
|
| Step 2. | (M-step). Maximize the likelihood of the complete data.
|
| Step 3. | If convergence is reached, set 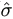 ² = σ2(p+1)
and ² = σ2(p+1)
and  = β (p+1);
otherwise increase p by unity and return to step 1. = β (p+1);
otherwise increase p by unity and return to step 1.
|
2.3 The Monte Carlo EM Algorithm
In general, the implementation of the EM Algorithm is not easy and computationally intensive, especially for the calculation of the conditional expectation (2.4) in the E-step. With the presence of censored data, it is rare to have a closed form for the conditional distribution, so the implementation becomes even more complicated. Thanks to the extreme complexities of implementation, we have to adopt more complex tools, such as Monte Carlo method. The Monte Carlo EM Algorithm (MCEM) is also advantageous in implementation of non-parametric or semi-parametric methods.
The Monte Carlo EM algorithm (Wei & Tanner, 1990; Tanner, 1996) is a Monte Carlo
implementation of the E-step to perform the integration in
equation (2.4). In particular, given the current estimation
 (p),
the MCEM algorithm corresponding to Definition 2.2 on page 24 is given as
(p),
the MCEM algorithm corresponding to Definition 2.2 on page 24 is given as
Definition 2.3
Define the general MCEM iteration  (p) →
(p) →  (p+1) as follows:
(p+1) as follows:
| E-step: | Given the simulation sample size m, the Monte Carlo E-step is given as |
| (1). | Draw a sample x(1), ..., x(m)
from conditional distribution k (x|y,  (p)). (p)).
|
| (2). | Let 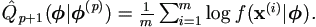 |
| M-step: | Choose  (p+1) to be a value of (p+1) to be a value of
  Ω which maximizes Ω which maximizes
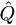 p+1. p+1. |
 (p+1), and the algorithm is iterated until it converges.
(p+1), and the algorithm is iterated until it converges.
Two important considerations regarding the implementation of this
Monte Carlo algorithm are the specification of m and monitoring
convergence of the algorithm. It is inefficient to start with a large
value of m when the current approximation to  may
be far from the true value. Rather, it is recommended that one
increase m as the current approximation moves closer to the true
value. One may monitor the convergence of the algorithm by plotting
(or simply examining a table of )
may
be far from the true value. Rather, it is recommended that one
increase m as the current approximation moves closer to the true
value. One may monitor the convergence of the algorithm by plotting
(or simply examining a table of )  (p) versus the
iteration number p. After a certain number of iterations, the plot
will reveal that the process has stabilized; that is, there will be
random fluctuation about the
(p) versus the
iteration number p. After a certain number of iterations, the plot
will reveal that the process has stabilized; that is, there will be
random fluctuation about the  =
= 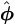 line. At this point, one may terminate the
algorithm or continue with a larger value of m that will further decrease the system variability.
line. At this point, one may terminate the
algorithm or continue with a larger value of m that will further decrease the system variability.
2.3.2 Derivatives in the MCEM Algorithm
The gradient (the first derivative, score function) and Hessian matrix (the second derivative) are of use in accelerating the EM algorithm and in specifying covariance matrix of the normal approximation (Hartley, 1958; Meilijson, 1989; Louis, 1982). Specifically, the gradient is given as
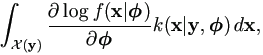
and the Hessian matrix is
 | (2.8) |
where the variance varx|y(.) is with respect to k(x|y, ) as
) as

Note that the integral in the last term is the expected score of complete data, which is equal to the observed score. Therefore it is 0 at MLE 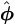 (see Tanner, 1996, pp.47-48).
(see Tanner, 1996, pp.47-48).
Given a sample x(1), x(2), ..., x(m)
from the current estimation to the conditional distribution k(x|y, ), approximate the gradient by
), approximate the gradient by

and the Hessian matrix by

where S( ) is the sample covariance matrix
for the m vectors
) is the sample covariance matrix
for the m vectors 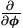 log ƒ(x(i)|
log ƒ(x(i)| ) with m-1 degrees of freedom.
) with m-1 degrees of freedom.
As a useful property of maximum likelihood estimator, the asymptotic
dispersion matrix of 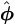 is always available and
given by the inverse of Fisher information matrix, which is the
opposite of Hessian matrix above. The covariance matrix of
is always available and
given by the inverse of Fisher information matrix, which is the
opposite of Hessian matrix above. The covariance matrix of
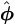 can be approximated by
can be approximated by
 | (2.9) |
It is worthwhile mentioning that all results here are in terms of expected derivatives from complete data, in stead of direct use of observed data, whose derivatives are usually difficult to handle in practice.