Find the angles of the right triangle ABC!
Solution:
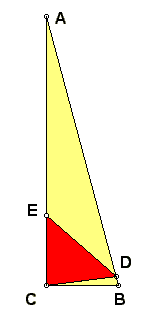
Let AB = c, BC = a, AC = b, c^2 = a^2 + b^2.
Then AD = AC = b, CE = a*b/c,
also AE = b - a*b/c, BD = c - b;
then area of BCD is s1 = 1/2 a*(c-b)(b/c),
area of ADE is s2 = 1/2 b*(b-a*b/c)(a/c),
s1 + s2 = 1/2 a*b*(1- a*b/c^2);
area of CDE is 1/2 a*b - s1 - s2 = 1/2 a*b (a*b/c^2);
hence (a*b/c^2)=1/4 =>
angle CAB = 15 deg, angle ABC = 75 deg.

