In the right triangle ABC,
(with right angle C,
and legs BC = a, and AC = b)
two chevians BD and CE meet at point F.
Construct the point F
such that area of triangle BFC
equals to area of quadrangle ADFE,
and these areas are maximal.
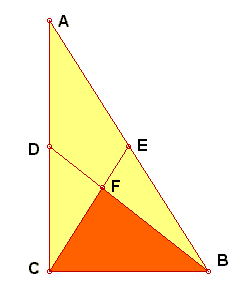
Answer see here.