Fractals
Buddhabrot

Lien entre le Mandelbrot et le Buddhabrot

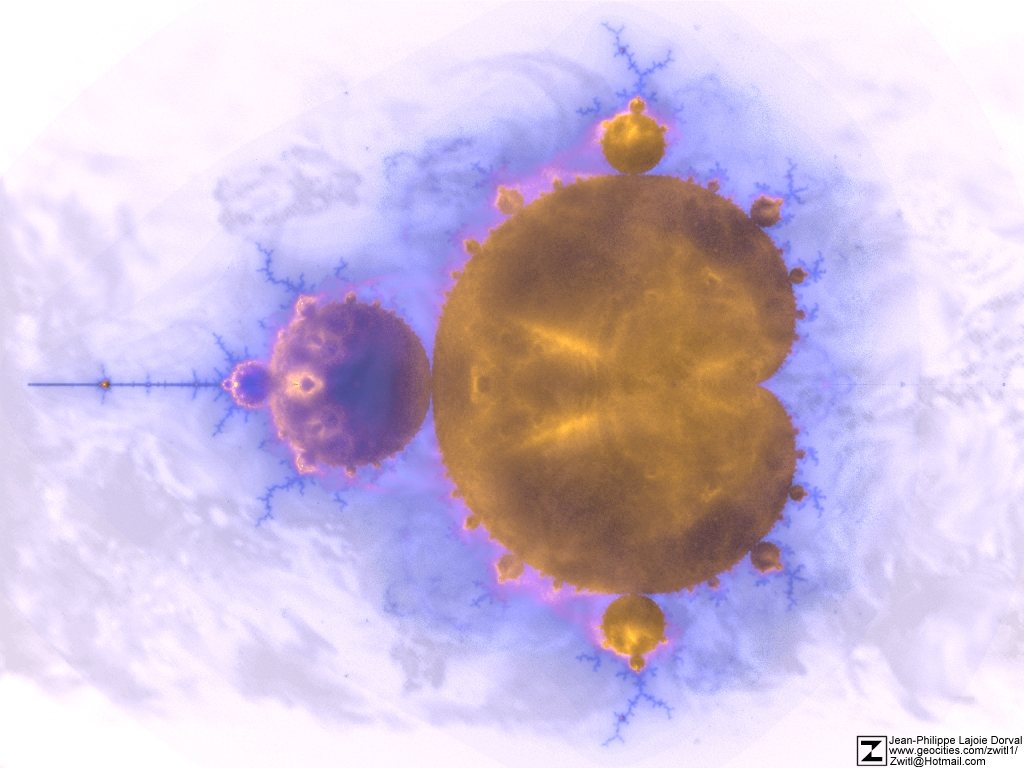
Le buddhabrot, au lieu d'afficher la vitesse de divergence de chacune des valeurs initiales C de l'équation Z²+C, illustre plutôt la fréquentation (ou la popularité) d'une région dans le Mandelbrot. La méthode utilisée pour générer l'image est de quadriller la zone dans laquelle se trouve le Mandelbrot, (de -2 à 1 en réel et de -1,5 à 1,5 en complexe) en itérant l'équation Z²+C pour chacun de ces points. Àchaque itération, on additionne 1 dans la matrice de l'image vis-à-vis le pixel qui correspond au résultat de Z²+C. La couleur est donnée en fonction la fréquentation du pixel le plus souvent visité. Ainsi, si un point a été fréquenté 200 fois et que le maximum a été de 500, le pixel aura la couleur à 40% de la palette. Si le gain est à 2, la couleur à 80% sera utilisée. Le gain sert à neutraliser l'effet des point trop souvent parcourus. Naturellement, je tient compte que la figure est symétrique afin d'acclélérer les calculs. Il existe une autre approche que de quadriller le mandelbrot. On peut choisir des points au hasard, mais l'image est peut précise si on utilise peu de point et on est à la mercie d'un mauvais générateur de nombres aléatoire.

En résumé, les région blanches sont les endroits les plus visité lors du calcul du mandelbrot. Pour des raison d'ordre estétique, l'image a été tournée de 90 vers la gauche. C'est le cas de toutes les images où l'axe de symétrie est vertical.

Si on supperpose les deux images on obtient le résultat suivant:

En bleu pâle, on retrouve les zones divergente du Mandelbrot, qui le devienne de moins en moins en devenant plus foncée. Le reste est la zone de convergence En orange, on a la contribution du buddhabrot. La section gauche du mandelbrot (la tête) est légèrement bleue, c'est le résultat du rouge créé par la coloration de la zone de convergence (en rouge dans l'image ci-haut à droite), sa couleur a des raison artistique.

Effet du nombre d'itérations effectuées

La majeure partie de l'image est causé par les points appartenant à la partie interne du mandelbrot, celle qui ne diverge pas après le nombre limite d'itération. Le nombre d'itération effectué a aussi une grande influence, car puisque les points qui convergent crées l'images, il n'y a pas de limite théorique à l'itération. Compte tenu que le calcul de ses points n'a de limite que celle que l'on impose, le resultat en dépend donc. Par contre, à force d'itérer, les résultats de l'équatoion Z²+C auront tendance à demeurer dans le même secteur, ce sont les attracteurs. On peut les visualiser comme les zones très blanches des images, tout particulièrement les "bijoux" du boudha lorsque l'on dépasse les 10000 itération.

Voici le Buddhabrot avec diverses limites d'itération et en utilisant 5000x5000 points.

10 itérations	20 itérations	50 itérations
100 itérations	200 itérations	500 itérations
1000 itérations	2000 itérations	5000 itérations
10000 itérations	20000 itérations	50000 itérations
	100000 itérations

Voici plus en détails le Buddhabrot, calculé avec 10000x10000 points et 50000 itérations

Variante de la nébuleuse (Nébulabrot)

En superposant le rendu de 3 buddhabrot ayant des nombres maximaux d'itérations différents et en assignant un canal RGB pour chacun d'entre eux, l'image obtenue permet de mieux voir les disparitées entre les 3 rendus. Les zones similaires sont blanches et les zones où un rendu est plus présent prend la couleur appropriée. Cette méthode est similaire aux images astronomique de la NASA où un couleur est associé à chaque photo prise à des longueurs d'ondes différentes. Cette variante a été proposée sur le site web de Melinda Green.

Colonnes de gas (Nasa)	Nebulabrot avec 100,200 et 500 itérations

Variante vectorielle (Vectorbrot)

Le site de Paul Bourke suggère une variante intéressante de l'algorithme du Buddhabrot. Au lieu de colorer le pixel en fonction de sa fréquentation, celui-ci est coloré par le module et l'angle du vecteur total des valeurs de C menant à ce pixel. En clair, on accumule les C pour chacun des pixels de l'image finale et on donne la couleur en fonction du total. En utilisant la représentation de couleur HSV, le Hue est donné par l'angle, la saturation est maximale et la vibrance est donnée par le module du vecteur divisé par le plus grand module trouvé (avec effet de gain). Le résultat est particulièrement coloré et donne, pour chaque pixel, la zone qui a contribué à sa popularité par la couleur (rouge est pour la tête, la partie supérieure est magentaet l'invérieure est verte. L'arrière est bleue

Pour ceux qui ne connaisse pas le code de couleur HSV:

• H est le Hue, soit un angle (de 0 à 360 degrés), où 0 est le rouge, 120 le vert et 240 le bleu
• S est la saturation, soit une valeur de 0 à 1 où 0 donne du gris et 1 donne la couleur pure donnée par le Hue.
• V est la vibrance, soit une valeur 0 à 1 où 0 donne du noir et 1 donne la couleur pure

Cela donne un cône renversé, où le noir est en bas et sur le pourtour supérieur, on a les couleurs.

Note: Mon algorithme HSV, pour les besoin de la cause, modifie la saturation si la vibrance dépasse 1. Ainsi, si la vibrance est de 2, elle devient 1 et la saturation est diminuée de 1, ce qui donne invariablement 0. On a donc du blanc.

Voici le résultat pour l'équation du Mandelbrot d'ordre 2 et 4:

Mandelbrot de deuxième ordre

Mandelbrot d'ordre 4

Variante de la séquence de création

Puisque mon algorithme génère le buddhabrot de gauche à droite en parcourant systématiquement toues les coordonnées intéressante du mandelbrot normal, il apparaît d'une manière particulière lorsqu'on effectue le rendu. En effet, certaines zone apparaissent avant d'autre. Si on compare avec el vectorbrot ci-haut, Les zones rouge apparaissent avec les oranges et les mauves. Puis viennent les vertes et les magentas et finalement les vertes et les bleues. On peut créer une animation avec cela. À toutes 25 colonnes dessinées (sur 15000), on sauvegarde l'image intermédiaire et on y supperpose en blanc le résultat des 150 dernières colonnes avec un dégradé (les colonnes sont graduellement moins lumineuses au fur et à mesure qu'on avance). On anime le toutet cla donne le résultat suivant pour une image. beauté de cet algorithme.