(last updated: Jan 02,
2009)
The
greenhouse
effect is responsible for raising the average temperature of the Earth
by 33°
C. Without it
the oceans would freeze right to the
equator, and there would be no complex life on Earth. The
burning of fossil fuels and other human activity
is
increasing the level of greenhouse gases in the atmosphere, which is
leading to increasing warming. On this page, the greenhouse effect is
explained
starting with simple
models, then advancing to more complex and scientifically accurate
descriptions.
A
glass greenhouse
stays warm mainly because the glass walls prevent the wind from
removing heat from the enclosed area, and prevent warm air
rising from inside the greenhouse to be replaced with
cooler air from above. The heat trapping
properties of the glass itself are relatively minor. A
glass
greenhouse has very little to tell us how the so-called "greenhouse
effect" on Earth actually works.
We
can
think of greenhouse gases as a "blanket", that allows energy from the
sun to pass through it and warm the Earth, but slows down the release
of energy from the Earth, similar to how a blanket keeps you warm on a
cold night. If you add another "blanket" (increase greenhouse
gas
levels) the Earth gets a little warmer. However, a real
blanket
works by slowing down (insulating) the transfer of
heat from your body. Insulation and convection have nothing to do with
how
greenhouse gases work.
A problem with this simple model arises when we realize that there is a
lot more water vapor in
the atmosphere then carbon dioxide. The amount of water vapor can vary
but averages around 0.4%, compared to less than 0.04% for carbon
dioxide. Water vapor also absorbs energy over a wider spectrum than
carbon
dioxide.
If our "blanket" is mostly water vapor with a few specks of carbon
dioxide, and the water is the better absorber, then doubling the amount
of carbon dioxide would seem to make little difference. But in fact
water vapor only contributes two thirds of
the greenhouse effect. That fact can only be understood by
discarding
the simple blanket model, and using a more scientifically sound
radiation balance model.
This
analogy is useful in the sense that addimg more blankets has a
diminishing effect on keeping you warm. The same is true for increasing
greenhouse gas levels.
We will begin with a world without any greenhouse
gases. The Earth receives its heat as visible light from the
sun. To
stay in temperature balance, it must radiate the same amount of
energy that it receives back into space, which it does at a longer
(infrared) wavelength. If the sun increases in intensity, the
surface of the Earth will warm, and it will radiate more energy back
into space until the temperature comes back into balance (at a higher level than before).
Now we will add greenhouse gases, but will (for the moment) assume the
entire atmosphere is the same temperature as the surface of the earth.
The Earth receives light from the sun, and tries to
radiate the heat (infrared radiation) back into space. Some
of
this infrared radiation will be absorbed by the new greenhouse gases,
which will, in turn, radiate the absorbed energy into space. But
because
these
gases are at the same temperature as the Earth's surface (averaged over
a period of time), they will
radiate the same amount of energy into space. The Earth will
lose
the same amount of energy, so the greenhouse gases will have little
effect
on
the temperature.
What went wrong? We did not describe the atmosphere properly.
Greenhouse gases are distributed throughout the atmosphere,
which
gets cooler with altitude. The key
point is the amount of energy a greenhouse gas radiates depends on its
temperature. Greenhouse gases near the surface have little
effect, because they
radiate at about the same temperature of as the Earth's surface [They may also transfer their
energy to other molecules in the atmosphere, causing local warming].
However, higher up in the atmosphere they are cooler, so they radiate
less energy. Thus the Earth as a whole radiates less energy than it
would have in the absence of greenhouse gases, and this gets a little
warmer. Most of the greenhouse effect takes
place high in the troposphere.
Greenhouse gases like carbon dioxide and methane are "well mixed",
meaning they have the same
concentration throughout the troposphere. However, water vapor is
different, which we observe whenever it rains or snows.
Colder air
holds less water vapor. Because the temperature of the
atmosphere
falls with
altitude, the concentration of water vapor decreases with height. Near
the top of the troposphere its concentration is less than that of
carbon dioxide.
So although there is a lot more water vapor than carbon
dioxide in total, there is relatively less water vapor where it matters
most. That is why water vapor only accounts for two thirds of the
greenhouse effect.
| The greenhouse effect
is governed by the following physical laws: |
| (1) |
Wien's
Law - The wavelength of energy emitted
from a body increases with decreasing temperature. |
| (2) |
Stefan-Boltzmann
- A body in space radiates an
amount of energy proportional to the fourth power of its temperature.
The warmer the body, the more energy is lost. |
| (3) |
Conservation
of Energy - The Earth must emit the
same amount of energy that it receives for its temperature to stay
constant. |
| (4) |
Lapse
Rate - The temperature of the atmosphere decreases with
altitude. |
| (5) |
Clausius
Clapeyron - The maximum
possible
concentration of water vapor
(absolute humitidy)
decreases exponentially with falling temperature and pressure, and thus
with altitude in the atmosphere. Relative humidity, the
fraction of
water vapor compared to the maximum possible at a given temperature,
also declines with altitude. In the lower troposphere,
saturation
vapor pressure increases by 7% for each degree K. [ref] |
| (6) |
Logarithmic Response
- The
radiative forcing of a greenhouse gas is proportional to the logarithm
of its concentration, for any concentration
that is likely to occur on Earth. |
| (7) |
Kirchhoff's
Law - Objects that absorb radiation
strongly at a given wavelength will emit strongly at the same
wavelength. |
|
All matter with a temperature above absolute zero emits radiation. The
hotter the substance, the more radiation it emits and the shorter the
average wavelength of the radiation emitted. Being
a hot
body,
most of the Sun's radiation has a short wavelength, around the visible
light
part of
the electromagnetic spectrum (Law 1). This energy heats the
Earth. In order to maintain a temperature balance, the Earth
must
radiate as much energy as it receives (Law 3). Being cooler
than
the
Sun,
this energy is in the form of longer wave infrared radiation
(Law 1). The emission spectrum rises quickly and falls slowly, but appears
as the shape of a bell curve on the logarithmic scale of the graph
below.
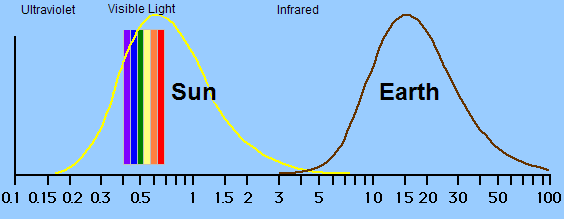
The greenhouse effect is caused by the fact that the atmosphere is
mostly
transparent to incoming shortwave solar radiation, but some gases
absorb part of
the longwave energy radiated back to space. Over 99% of the
atmosphere
consists of nitrogen and oxygen, both two-atom molecules with no
ability to absorb infrared radiation. The remaining fraction
of
a percent consists of more complex molecules such as water vapor,
carbon dioxide, methane and others, which are responsible for the
greenhouse effect.
Molecules with more than two atoms have more than one chemical bond.
Vibrations in a gas molecule are like vibrations of a piano string in
that they are sensitive to frequency. This is because, like a piano
string, a gas
molecule will only vibrate at its “ringing”
frequency.
All of their bonds ring together rather than each bond ringing
with its own characteristic frequency.
Water is a molecule that is bent when in its lowest energy
state. Hydrogen atoms hold their
electrons more
loosely than oxygen atoms, and so each hydrogen has a slightly positive
charge (marked using the lowercase greek letter delta, as
δ+).
The oxygen end of the molecule has a slight negative charge. A rotating
an H2O
molecule would oscillate the
electric field and generate light. There are several modes of vibration
of the water molecule, including a symmetric stretch and a bend. These
modes are also infrared active.

The CO2
molecule is shaped in a
straight line with carbon in the middle. It is a symmetric molecule;
the oxygen atom on one end pulls the electrons just as tightly as the
other oxygen on the other end. Therefore rotating the molecule
at rest has no effect on the electric field. The symmetric
stretch also has no effect. However, there are two modes of vibration
which do generate an
asymmetry in the electric field. One is an asymmetric stretch, and the
other is a bend. The bend is the most climatically important one. [ref]
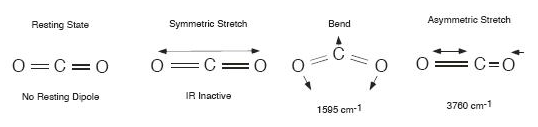
The presence of greenhouse gases means that instead of radiating energy
from its surface, the Earth radiates energy
back into space from higher up in the atmosphere. Convection
is always lifting air from the ground to
high altitudes in
the troposphere, causing the air to cool by expansion as it rises. This
is the basic reason that temperature goes down with height in the
troposphere (Law 4). As a result, the infrared radiation that
escapes to space
comes more from the
higher, colder parts of the atmosphere. Since the emission rate of
infrared radiation
increases to the fourth power of temperature (Law 2), the radiation
from
these layers is much feebler than the radiation that would escape from
the ground. If the concentration of greenhouse
gases is
increased, the average radiation occurs from a higher altitude, so less
energy is lost
and more is retained (Law 3).
If atmosphere had a constant density with a
discrete top, its temperature at the top would be the same as at the
bottom. It would radiate at the same temperature no matter
how
much of it was greenhouse gas.
The greenhouse effect only
takes
place because of the atmosphere's temperature gradient.
Given that water vapor is about 1% of the atmosphere as compared to
0.037% for carbon dioxide, one might think that the relative difference
made by carbon dioxide is small. This is made worse by the
fact
that on a per-molecule basis water vapor is 3.3 [need a reference for this]
times as effective as
carbon dioxide. But water vapor has one critical distinction
- it
is a liquid at a moderate temperature and pressure. Because
it
precipitates out of the atmosphere, its concentration is not
constant. Instead, the atmosphere cools with
altitude (Law
4),
and
the ability to hold water decreases rapidly with temperature (Law 5),
so water vapor concentration decreases rapidly with altitude.
At
the top of
the troposphere, where most of the greenhouse effect takes place, there
is less water vapor than carbon dioxide. It turns out that
water
vapor is responsible for about 65% of the greenhouse effect, while
carbon
dioxide and other greenhouse gases are responsible for the rest.
See also this
discussion.
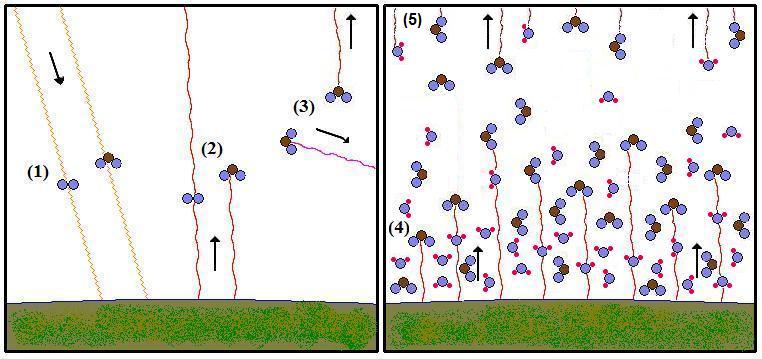 |
- Shortwave radiation (mostly visible light) from the
sun
reaches the Earth and warms it, unaffected by passing through the
oxygen and carbon dioxide
molecules in the
atmosphere [A carbon dioxide molecule is
straight, not bent].
- The Earth radiates longer wave (infrared) radiation
back to
space. The oxygen molecule on the left is transparent to this
radiation, but the carbon dioxide molecule on the right absorbs
radiation that is at a specific wavelength.
- The carbon dioxide molecule re-radiates the energy
at
a
random angle. Kirchhoff's Law [Law 7] tells us it will most likely emit
at the same wavelength it absorbed from. Some of
them will
radiate the energy into space. Its altitude (thus
temperature) will determine the amount of energy it radiates.
- In the right panel, the concentration of carbon
dioxide and water vapor
has
increased. This does not result in a proportional increase in
the
greenhouse effect because not all molecules will have the opportunity
to absorb radiation. The molecules that radiate into space are only
slightly higher than before. Effectively, the average
altitude at
which the Earth radiates from has been raised. Therefore the
warming only
increases logarithmically with greenhouse gas concentration.
That means each doubling has the same impact as the previous
one.
- Radiation escapes into space from the upper
troposphere.
The atmosphere is thinner and cooler, so the radiating
temperature is lower. Carbon dioxide has the same
concentration
throughout the troposphere, but water vapor concentration decreases
with altitude. So while there is much more water vapor near
the
surface, there is relatively less higher up, so carbon dioxide makes a
much larger contribution to the greenhouse effect than its average
concentration would suggest.
|
The picture below shows actual measurements of longwave radiation
reaching the surface of the Earth due to the greenhouse effect.
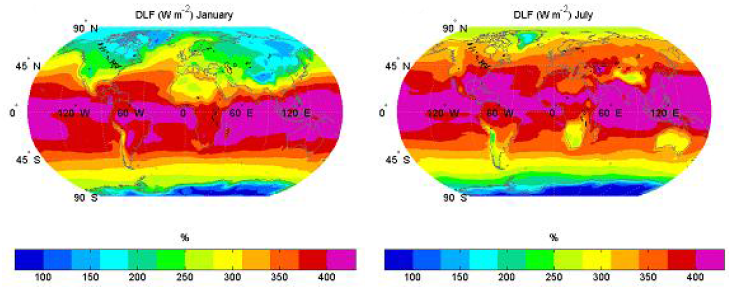
Geographical distribution of model downwelling longwave
flux
(DLF), at the surface for January and July, averaged over
1984–1993. [ref]
A greenhouse gas does not absorb all thermal radiation, it absorbs only
certain wavelengths. When the absorbing wavelengths of
different
greenhouse gases overlap, the effectiveness of each gas is reduced.
From here:
Carbon dioxide has three absorption bands at wavelengths of 4.26,
7.52, and 14.99 micrometers (microns). The Earth's emission spectrum,
treated as a black body (no atmospheric absorption), peaks at between
15 and 20 microns, and falls off rapidly
with decreasing wavelength. As a result, the carbon dioxide absorption
bands at 4.26 and 7.52 microns contribute little to the absorption of
thermal radiation compared to the band at 14.99 microns. Natural
concentrations of carbon dioxide are great enough that the atmosphere
is opaque even over short distances in the center of the 14.99 micron
band. As a
result, at this wavelength, the radiation reaching the tropopause from
above and below the tropopause is such that the net flux is close to
zero.
If
this were the whole story, adding more carbon dioxide to the atmosphere
would contribute nothing to the greenhouse effect and consequently
could not cause a rise in the Earth's temperature. However, additional
carbon dioxide does have an influence at the edges of the 14.99 micron
band. Because of this marginal effect, the change in forcing due to a
change in carbon dioxide concentration is proportional to the natural
logarithm of the fractional change in concentration of this gas.
Specifically, [IPCC
6.3.5] gives
dF =
5.35 ln (C/Co)
W/m2
where
dF is the change in forcing, and Co
and C are the initial and final
carbon dioxide concentrations. This approximation breaks down for very
low concentrations (around 1 ppm) and for concentrations greater
than 5% (50,000 ppm), but
is valid in the range of practical interest. The Earth's temperature is
therefore relatively insensitive to changes in carbon dioxide
concentrations, a doubling leading to a dF of only 3.7 W/m2.
There is some overlap between carbon dioxide and water vapor in the 15
micron portion of the spectrum where the Earth's infrared radiation is
at is peak. But note that the overlap of the water vapor and carbon
dioxide bands only occur in the lower atmosphere, because increased
atmospheric pressure causes the absorption specturm of
longwave
radiation by water vapor to broaden. Higher in the atmosphere, where
there is little water vapor, there is no overlap of the absorption
bands, as can be seen in the above chart for 11 km above the surface at
15 microns.
 |
Carbon dioxide is the most frequently
mentioned greenhouse gas, but water vapor absorbs infrared (heat)
radiation much more strongly. Carbon dioxide is significant because it
closes a “window” that would otherwise allow
certain infrared wavelengths to escape the Earth’s water
vapor blanket. The graph at left shows the percentage of energy
absorbed in a clear tropical sky by water vapor (green) and carbon
dioxide (brown). (Graph by Robert Simmon, based on model data from the
NASA GSFC Laboratory for Atmospheres) [ref]
|
Various atmospheric constituents absorb electromagnetic
radiation. The
important absorbing gases and their absorption efficiency as a function
of wavelength is shown on the right.
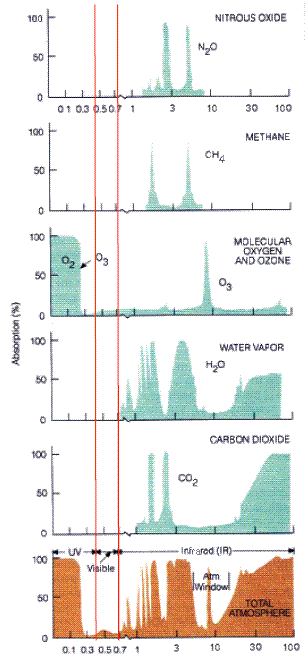
Note the strong oxygen absorption in the UV part of the spectrum and
that of water vapor, which absorb effectively in large sections of the
IR wavelength range.
CO2 absorption band overlaps a gap in the water vapor band (referred to
a “window”) hence its importance.
[The
horizontal wavelength
scale on this graph is clearly incorrect. The second carbon dioxide
peak, aligned with the gap in water vapor, shoud be at 15 microns.]
From this lecture on the Physics
and Chemistry of the Earth’s Climate System |
 |
From the IPCC
Climate Change 2001 Report:
If the amount of carbon dioxide were
doubled instantaneously, with
everything else remaining the same, the outgoing infrared radiation
would be reduced by about 4 W/m2.
In other words, the
radiative forcing corresponding to a doubling of the CO2
concentration would be 4 W/m2.
To counteract this imbalance,
the temperature of the surface-troposphere system would have to
increase by 1.2°C (with an accuracy of ±10%), in the
absence
of other changes. In reality, due to feedbacks, the response of the
climate system is much more complex. It is believed that the overall
effect of the feedbacks amplifies the temperature increase to 1.5 to
4.5°C. A significant part of this uncertainty range arises from
our
limited knowledge of clouds and their interactions with radiation. To
appreciate the magnitude of this temperature increase, it should be
compared with the global mean temperature difference of perhaps 5 or
6°C from the middle of the last Ice Age to the present
interglacial.
...
Carbon dioxide absorbs infrared radiation in the middle of
its 15 mm
band to the extent that radiation in the middle of this band cannot
escape unimpeded: this absorption is saturated. This, however, is not
the case for the band’s wings. It is because of these effects
of
partial saturation that the radiative forcing is not proportional to
the increase in the carbon dioxide concentration but shows a
logarithmic dependence. Every further doubling adds an additional
4 W/m2
to the radiative forcing.
The logarithmic behavior of CO2
in Earth's atmosphere applies between 1 ppm
to around 5% (50,000 ppm). At very low
concentrations (say, around 1 ppm) bands are unsaturated
and Outgoing Longwave Radiation
becomes more sensitive to CO2
than in the logarithmic range. At
sufficiently high concentrations the absorption starts to be
dominated by weak bands that have a
different probability distribution than the bands that dominate in the
present climate.
CO2 opacity
for the present Earth is dominated by the 15 micron band
group. The envelope of the absorption strength in this group tails off
roughly exponentially from the center of the group, once the lines are
broad enough to overlap significantly within each sub-band of the
interval, and the resulting probability distribution of absorption can
be shown to give rise to the logarithmic behavior. However, the
exponential envelope is only approximate, and only extends a certain
distance out from 15 microns, so once you put in enough CO2 you get out
of the logarithmic range. [ref]
It is instructive to compare the Earth with some other planets that
have an atmosphere, to get a large scale perspective on the
significance of the greenhouse effect.
The non-greenhouse temperature (T) of a planet is a
function of its
distance (d) from the sun (in astronomical units) and how much of that
energy it absorbs (1 -
albedo), as shown
by the equation
T =
279°
K
[ (1 - albedo)/d2)
]1/4
The greenhouse temperature can also be calculated by multiplying the
Atmospheric Lapse Rate (how fast the atmosphere gets colder with
altitude) by the mean Emission Altitude (the average height from which
energy is radiated into space), according
to the equation
Greenhouse Difference = Lapse
Rate * Emission Altitude
The table below illustrates the greenhouse effect on the Earth and some
of its neighbors in space. The solar constant is the amount
of
energy reaching the planet. Albedo is how much light is
reflected.
The Greenhouse Effect on the Inner Planets
Planet
or
Satellite |
Solar
Constant |
Albedo |
CO2 Factor |
No
Greenhouse
Temperature |
Actual
Average
Temperature |
Greenhouse
Difference |
Atmospheric
Lapse Rate |
Emission
Altitude |
| Venus |
2643 W/m2 |
72% |
180,000 |
-43°
C |
470°
C |
513°
C |
7
°C / km |
70
km |
| Moon |
1370 W/m2 |
7% |
0 |
0°
C |
0°
C |
0°
C |
- |
- |
| Earth |
1370 W/m2 |
30% * |
1 |
-18°
C |
15°
C |
33°
C |
5.5
°C / km |
6
km |
| Mars |
593 W/m2 |
25% |
1.27 |
-63°
C |
-59°
C |
4°
C |
5
°C / km |
1
km |
* The value of 33°
C of greenhouse warming for Earth (cited everywhere) is based
on today's albedo. But much of that albedo comes
from
clouds, which would not exist if there was no water vapor, and which
also have an insulating effect that is not taken into account.
So if water did not exist on the Earth, the albedo would be
lower, and its temperature larger than -18°
C. But water does exist, so the 33°
C is a realistic value for today's conditions.
Venus has a
thick carbon dioxide atmosphere and a huge
greenhouse effect. The
logarithmic relationship between CO2
and
radiative forcing only holds for low concentrations, less than 20% of
the Earth's atmosphere. Carbon
dioxide absorption
bands expand with increased
atmospheric
pressure (collisional broadening) and higher temperatures (doppler
broadening). A lot of weak bands that are inconsequential on
Earth become dominant in determining the changes in Outgoing
Longwave Radiation [ref]. Note
that because of its reflective clouds, its
no-greenhouse temperature is actually lower than that of the Earth
despite
receiving twice the sunlight. Clouds on Venus are composed mainly of
sulfurinc acid, which (unike water vapor clouds) has no greenhouse
effect. They do reflect infrared radiaion, so they also contribute
to
temperature by their insulating effect. For more on Venus, see [ref].
The atmosphere of Mars
is 96% CO2,
about 254 times the proportion on Earth. Its atmospheric mass
is
2.5 x
1019
g, compared to Earth's 5.1 x 1021
g, or 1/200 as much, so Mars has 1.27 times more CO2 than
Earth. Mars has one quarter the surface area of Earth, so it
effectively has five times the level of greenhouse gas. It
receives less
than half the solar energy, and gets 4°
C of extra warming.
| Planetary Temperature
Calculator: T =
280°
K
[ (1 - albedo)/d2)
]1/4 |
|
The direct increase in radiative forcing (dE) caused by an
increase in carbon dioxide levels, in watts per square meter, can be
found by the equation
dE =
5.35 ln (C/Co) W/m2
where C is
the new carbon dioxide level (in parts per million, or ppm) and Co is the
starting carbon dioxide level. For example, CO2
concentration has risen from 270 to 370 ppm, so the
equation gives 5.35 x
ln(370/270) = 1.7 W/m2
raw forcing.
| Radiative
Forcing Calculator |
|
|
|
Return
to the Climate Change Main Page










