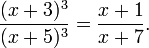Home Page Sutras Addition Subtraction Multiplication

Vedas and Mathematics

Sutra 5: If the Samuccaya is the same it is zero

This formula is useful in solution of several special types of equations that can be solved visually. The word samuccaya has various meanings in different applications. For instance, it may mean a term which occurs as a common factor in all the terms concerned. A simple example is equation "12x + 3x = 4x + 5x". Since "x" occurs as a common factor in all the terms, therefore, x = 0 is a solution. Another meaning may be that samuccaya is a product of independent terms. For instance, in (x + 7) (x + 9) = (x + 3) (x + 21), the samuccaya is 7 × 9 = 3 × 21, therefore, x = 0 is a solution. Another meaning is the sum of the denominators of two fractions having the same numerical numerator, for example: 1/ (2x − 1) + 1/ (3x − 1) = 0 means we may set the denominators equal to zero, 5x - 2 = 0.



Yet another meaning is "combination" or total. This is commonly used. For instance, if the sum of the numerators and the sum of denominators are the same then that sum is zero. Therefore,




{2x+9 \over 2x+7}={2x+7 \over 2x+9}.



Therefore, 4x + 16 = 0 or x = −4.



This meaning ("total") can also be applied in solving quadratic equations. The total meaning can not only imply sum but also subtraction. For instance when given N1/D1 = N2/D2, if N1 + N2 = D1 + D2 (as shown earlier) then this sum is zero. Mental cross multiplication reveals that the resulting equation is quadratic (the coefficients of x2 are different on the two sides). So, if N1 − D1 = N2 − D2 then that samuccaya is also zero. This yields the other root of a quadratic equation.



Yet interpretation of "total" is applied in multi-term RHS and LHS. For instance, consider




{1 \over x-7}+{1 \over x-9}={1 \over x-6}+{1 \over x-10}.



Here D1 + D2 = D3 + D4 = 2x − 16. Thus x = 8.



There are several other cases where samuccaya can be applied with great versatility. For instance "apparently cubic" or "biquadratic" equations can be easily solved as shown below:




(x − 3)3 + (x − 9)3 = 2(x − 6)3.



Note that x − 3 + x − 9 = 2 (x − 6). Therefore (x − 6) = 0 or x = 6.

This would not work for the apparently quadratic (x − 3)2 + (x − 9)2 = 2(x − 6)2, which has no real or complex solutions.



Consider




{(x+3)^3 \over (x+5)^3}={x+1 \over x+7}.



Observe: N1 + D1 = N2 + D2 = 2x + 8. Therefore, x = −4.



This formula has been extended further.

Home Page Sutras