Circunferencia
| RESEÑA HISTORICA | |
| GEOMETRIA | |
| CONCEPTOS | |
| BIBLIOGRAFIA | |
| CREDITOS |

|
ECUACIÓN DE LA CIRCUNFERENCIA
DEFINICIÓN. Circunferencia es el lugar geométrico de un punto que se mueve en un plano de tal manera que se conserva siempre a una distancia constante de un punto fijo de un plano.
El punto fijo se llama centro de la circunferencia, y la distancia constante se llama radio.
Y
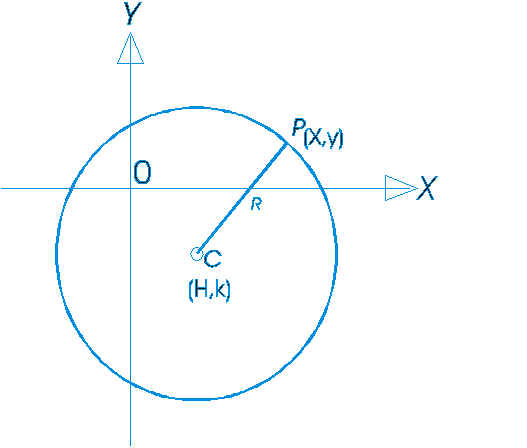
ECUACIÓN ORDINARIA
TEOREMA 1. La Circunferencia cuyo centro es el punto (h,k) y cuyo radio es la constante r, tiene por ecuación:
(x – y) 2 + (y – k)2 =r2
DEMOSTRACIÓN:
Sea P (x,y) un punto cualquiera de la circunferencia de centro C (h,k) y radio r . Entonces, por definición de circunferencia, el punto P debe satisfacer la condición geométrica
/CP/ = r (1)
la cual está expresada analíticamente por la ecuación de la distancia entre dos puntos dados; el centro y el punto (x,y)
raiz de (x-h)2 + (y-k)2 = r ,
de donde,
(x – h)2 + (y – k)2 = r 2 (2)
Recíprocamente, si se le dan otros valores a las coordenadas en x y y que satisfagan la ecuación 2 y se verifique la igualdad
(x1 – h)2 + (y1 – k)2 = r 2
Aquí se despeja la raíz cuadrada,
raiz de (x1-h)2 + (y1-k)2 = r
que es la expresión analítica de la condición geométrica (1) aplicada al punto P1 (x1,y1). Por tanto, demostrados los teoremas directo y recíproco, resulta que 2 es la ecuación buscada.
Para el caso particular de que el centro esté en el origen (0,0) la ecuación queda de la siguiente manera:
(x – h)2 + (y – k)2 = r 2
(x – 0)2 + (y – 0)2 = r 2
x2 + y2 = r 2
ECUACIÓN GENERAL
Si desarrollamos la ecuación ordinaria
(x – h)2 + (y – k)2 = r 2 (1)
obtenemos
x2 + y2 – 2hx – 2ky + h2 + k2 – r2 = 0
lo cual puede escribirse en la forma
x2 + y2 + Dx + Ey + F = 0 (2)
en donde
D = -2h , E = -2k y F = h2 + k2 – r2
Se deduce por lo tanto, que la ecuación de una circunferencia puede escribirse en la forma general de la ecuación. El problema que presenta ahora es averiguar si, recíprocamente, toda ecuación de la forma general (2) representa una circunferencia. Para contestar esta pregunta, pasaremos de la forma (2) a la forma (1) empleando el método de completar cuadrados. Ordenando los términos de (2), resulta
(x2 + Dx) + (y2 + Ey) = -F
y sumando D2 /4+ E2 /4 a ambos miembros, obtenemos
(x2 + Dx + (D2/4)) + (y2 + Ey +( E2/4) ) =( D2 + E2 - 4F)/4
de donde,
(x + D/2)2 + (y + E/2)2 =( D2 + E2 - 4F)/4 (3)
Comparando las ecuaciones (1) y (3), vemos que depende del valor del segundo miembro de (3) el que (3) represente o no una circunferencia. Hay tres casos posibles por considerar:
a) Si D2 + E2 - 4F > 0, la ecuación (3) representa una circunferencia de centro en el punto (-D /2, -E/2).
Y radio igual a raiz de (D2 + E2 – 4F)/2
b) Si D2 + E2 – 4F = 0 , la ecuación (3) se dice, con frecuencia, que representa una circunferencia de radio cero; se dice también que es un círculo punto o círculo nulo. La ecuación representa un solo punto de coordenadas (-D /2, -E/2)
c) Si D2 + E2 – 4F <0 , la ecuación (3) se dice que representa un círculo imaginario; en este caso no representa un lugar geométrico.
Por conclusión tenemos que la ecuación x2 + y2 + Dx + Ey + F = 0 representa una circunferencia de radio diferente de cero, solamente si
D2 + E2 - 4F > 0
Las coordenadas del centro son, entonces, (-D/2 , -E/2) y el radio es raiz de ( D2 + E2 – 4F)/2
Posiciones Relativas De Una Recta Con Respecto a una Circunferencia
En relación con la circunferencia, una recta puede ser
Secante
Si tiene dos puntos de contacto con la circunferencia . b: secante. Con lo cual podemos deducir que es una línea que a diferencia de la tangente sobre pasa el limite de la circunferencia acercándose mas al centro por lo tanto su distancia OM al centro de la circunferencia es menor que la del radio.
OM
Ver Animación
Tangente
Si solo tiene un punto de contacto con la circunferencia . a : tangente a C (O;r) en N. Con lo que vemos que ese punto que toca de la circunferencia, al igual que todos los puntos que la componen equidistan del centro, con esto la distancia ON al centro de la circunferencia es igual al radio.
ON=r
Ver Animación
Exterior
Es la linea que o tiene ningún punto en común con la circunferencia. C es una recta exterior a C(O;r).Aquí sería al revés que la secante ya que difiere de la distancia del radio pero en el sentido que dista más que este. Su distancia OP al centro de la circunferencia es mayor que el radio.
OP>r
Posiciones relativas de dos circunferencias.
Son circunferencias pueden ser:
Concéntricas
Son circunferecias que tienen el mismo centro y distinto radio. En geometría analítica lo podríamos poner de esta manera a las dos circunferencias.
- r=(h-x)2 + (k-y)2
- r1=(h-x1)2 + (k-y1)2
Circunferencias concéntricas
C(O;r) y C(O;r’) son concéntricas
Ver Animación
Excéntricas interiores
Cuando estando una dentro de la otra, no tienen el mismo centro ningún punto en común.
C(O;r) y C(O’;r’) son concéntricas interiores
Ver Animación
La distancia entre los centros de dos circunferencias interiores es menor que la diferencia de los radios.
Ejemplo: OO’
C(O;r) y C(O’’;r’’) son excéntricas exteriores
Ver Animación
Tangentes exteriores
Cuando , estando una fuera de la otra, tienen un punto en común o de contacto.
C(O;r) y C(O’;r’) son tangentes exteriores en A
Ver Animación
La distancia entre los centros es igual a la suma de los radios.
Ejemplo: OO’= r + r’
Ver Animación
Tangentes interiores
Cuando estando una dentro de la otra , tienen un punto único de contacto.
Ver Animación
C(O;r) y C(O’;r) son tangentes interiores en Q
La distancia entre los centros de dos circunferencias tangentes interiores es igual a la diferencia de los radios.
Ejemplo OO = r - r’
Secantes
Tienen dos puntos de contacto.
C(O;r) y C(O’;r’) son secantes en M y N
La distancia entre los centros de dos circunferencias secantes es menor que la suma de sus radios , pero mayor que su diferencia.
Ejemplo: OO’
Ver Animación 1 | Ver Animación 2
Exteriores
Cuando estando fuera de la otra , no tienen ningún punto de contacto.
La distancia entre los centros de dos circunferencias exteriores es mayor que la suma de los radios.
Ejemplo: OO’ > r + r’
Angulo central
Es el ángulo que tiene su vértice en el centro de la circunferencia y sus lados son dos radios.
Ejemplo: a.
Relaciones entre arcos , cuerdas y ángulos centrales.
| En dos circunferencias iguales o en una misma , a cuerdas iguales se les oponen arcos y ángulos centrales iguales. | |
| En dos circunferencias o en una misma , a arcos iguales se le oponen cuerdas y ángulos centrales iguales. | |
| En dos circunferencias o en una misma circunferencia , a ángulos cent4rales iguales se les oponen arcos y cuerdas iguales. |
Ver animación
Ángulo inscrito a una circunferencia
Se llama ángulo inscrito en un arco de circunferencia al que tiene su vértice en un punto cualquiera de la circunferencia y su lados pasan por los extremos del arco.
MPN ángulo inscrito ; O e al lado del ángulo MPN está inscrito en MPN y abarca MN
ABC ángulo inscrito; O interior al ángulo ABC está inscrito en el arco AC que contiene
al punto B; o sea ABC y abarca AC .
A todo ángulo inscrito le corresponde un ángulo central que tiene su vértice en el centro de la circunferencia y cuyo lados son radios que pasan por los extremos del arco
b ángulo central correspondiente al ángulo inscrito a.
w ángulo central correspondiente al ángulo inscrito p .
Propiedades del ángulo inscrito
- Todo ángulo inscrito en un arco de circunferencia vale la mitad del ángulo central que le corresponde.
- Todos los ángulos inscritos que abarcan un mismo arco son iguales.
- Los ángulos inscritos que abarcan una semicircunferencia son rectos.}
e ángulo inscrito
b ángulo central correspondiente.
e = b’ / 2
a abarca el AG
b abarca el AG
w abarca el AG
b= 1800 por ser llano
a= b’/2 por ser ángulo inscrito que abarca el mismo arco.
a= 90o
Ver Animación 1 | Ver Animación 2 | Ver Animación 3
Ángulo semiinscrito a una circunferencia
El ángulo semiinscrito en un arco de circunferencia tiene su vértice en uno de los extremos del arco ; uno de sus lados pasa por el otro extremo y el otro lado es tangente a la circunferencia en el vértice.
Ver Animación 1 | Ver animación 2
e ángulo semiinscrito.
A todo ángulo semiinscrito le corresponde un ángulo central que tiene su vértice en el centro de circunferencia y sus lados pasan por los extremos del arco.
w ángulo central que le corresponde a e
Propiedades del ángulo semiinscrito:
- Todo ángulo semiinscrtio en un arco de circunferencia es igual a la mitad del ángulo central correspondiente.
- El ángulo inscrito y el ángulo semiinscrito en un mismo arco de circunferencia son iguales.
- Los ángulos semiinscrito en un mismo arco de circunferencia son iguales entre si
e ángulo semiiincsrito
w ángulo central correspondiente
Ver Animación 1 | Ver Animación 2 | Ver Animación 3
e ángulo seminscrito en PQR
a ángulo semiinscrito en PQR
e = b’ /2
a = b’ /2
Como ambos tienen el mismo ángulo central, son iguales , es decir:
e=a
Trazado de tangentes a una circunferencia desde un punto exterior
Trazar desde el punto T las tangentes a la C(O;r).
Se une T con O y TO es el diámetro de una circunferencia de centro P y radio PO.
Para hallar el centro P, se traza la mediatriz del segmento TO. Al trazar la C(P;PO) , está corta a la C(O;r) en dos puntos S y Q. Uniendo T y S y con Q , quedan construidas las tangentes TS y TQ
Ver Animación