 |
 |
 |
 |
 |
introduction
A special type of pandiagonal magic square was described in an 1897 paper by Eamon McClintock of Toronto University. He used a special square array called a McClintock square as an aid in their construction. He also showed that there was a one-to-one correspondence between the most perfect magic square and the McClintock square.
Recently Dr. Ollerenshaw, looking for a way to enumerate at least a sub-set of pandiagonal magic squares, realized that there was a way to enumerate all McClintock squares of a given order. She refined the definition of this square and renamed it reversible. The resulting magic square she called Most-Perfect (with a hyphen). She was 74 years old when she published her first paper on Most-perfect magic squares (in 1986). She published at least two other papers on the subject.
In 1998, Dr. Ollerenshaw co-authored a book on this subject with Dr. David Brée. Dr. Brée is Professor of Artificial Intelligence at the University of Manchester (the University which Dame Ollerenshaw was associated with).
Dr. Brée's main contributions to the book was to change the method of construction, which led to a simpler method of enumeration, and to find and then prove the equation for the new method of enumerating ALL doubly even squares.
McClintock, E. (1897) On the most perfect forms of magic squares, with methods for
their production. American Journal of Mathematics 19 p.99-120.
Ollerenshaw,K. (1986) On ‘most perfect’ or ‘complete’ 8 x 8
pandiagonal magic squares. Proceedings of the Royal Society of London A407,
p.259-281
Kathleen Ollerenshaw and David Brée, Most-perfect Pandiagonal Magic Squares, Institute
of Mathematics and its Applications, 1998, 0-905091-06-X
On this page I will attempt to present a simplified introduction to this type of magic
square using mostly material from the above book..
See also Ian Stewart, Mathematical Recreations column, Scientific American, Nov. 99,
p.122-123.
Features of Most-perfect magic squares
Features of a reversible square.
Transformation of Reversible Squares to Most-Perfect magic Squares
Number of principle reversible squares and most-perfect magic squares
Addendum - October, 2006 - Most-perfect Multiply magic squares
Addendum-2 - November, 2006 - Most-perfect ?
Most-perfect magic cubes posted July, 2006 (on another server)
Most-perfect Bent diagonals posted April 4, 2007
|
All 48 pandiagonal magic squares of order-4 are most-perfect! For other orders, not all pandiagonal magic squares are most-perfect. The 4 corner cells of any square array of cells in an order-4 most-perfect magic square sum to S. |
Definition
Additional feature
Two integers 1/2n along any row, with the left integer in an even column, have the
same sum. The same is true when the left integer is in an odd column. These two sums (for
evens and odds) sum to 2T. This feature is useful in proving that any most-perfect magic
square can be transformed into a reversible square.
| Note:
Note2: |
For mathematical convenience, the authors use
the series from 0 to n2-1. In that case S=n(n2-1)/2, T = n2-1. I have chosen to use the series from 1 to n2 to be consistent with the definition of a normal magic square with S=n(n2+1)/2. I use the symbol S to indicate the magic sum and T to indicate the value of n2 + 1) which the authors indicates with S. |
Higher dimensions
Aale de Winkel reports that these same features also apply to higher dimension
magic figures. Go to his magic objects site from my links page.
|
Definition
Reversible squares can be grouped into sets in which all squares can be transformed from one to another. There are Mn=2n-2{(1/2n)!}2 essentially different squares in each set. There is a unique principle reversible square in each set in which all
the rows, reading left to right , and all the columns reading top to bottom, contain
integers in ascending order, and the top row begins with the integers 1and 2. |
||||||||||||||||
|
|||||||||||||||||
|
![]()
The first set of 16 essentially different reversible squares for order-4.
The principle reversible square is the one in the top left corner.
|
1 |
2 |
3 |
4 |
.... |
1 |
2 |
3 |
4 |
.... |
5 |
6 |
7 |
8 |
.... |
5 |
6 |
7 |
8 |
|
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
1 |
2 |
3 |
4 |
13 |
14 |
15 |
16 |
|||
|
9 |
10 |
11 |
12 |
5 |
6 |
7 |
8 |
13 |
14 |
15 |
16 |
1 |
2 |
3 |
4 |
|||
|
13 |
14 |
15 |
16 |
13 |
14 |
15 |
16 |
9 |
10 |
11 |
12 |
9 |
10 |
11 |
12 |
|||
|
. |
||||||||||||||||||
|
1 |
3 |
2 |
4 |
1 |
3 |
2 |
4 |
5 |
7 |
6 |
8 |
5 |
7 |
6 |
8 |
|||
|
5 |
7 |
6 |
8 |
9 |
11 |
10 |
12 |
1 |
3 |
2 |
4 |
13 |
15 |
14 |
16 |
|||
|
9 |
11 |
10 |
12 |
5 |
7 |
6 |
8 |
13 |
15 |
14 |
16 |
1 |
3 |
2 |
4 |
|||
|
13 |
15 |
14 |
16 |
13 |
15 |
14 |
16 |
9 |
11 |
10 |
12 |
9 |
11 |
10 |
12 |
|||
|
. |
||||||||||||||||||
|
2 |
1 |
4 |
3 |
2 |
1 |
4 |
3 |
6 |
5 |
8 |
7 |
6 |
5 |
8 |
7 |
|||
|
6 |
5 |
8 |
7 |
10 |
9 |
12 |
11 |
2 |
1 |
4 |
3 |
14 |
13 |
16 |
15 |
|||
|
10 |
9 |
12 |
11 |
6 |
5 |
8 |
7 |
14 |
13 |
16 |
15 |
2 |
1 |
4 |
3 |
|||
|
14 |
13 |
16 |
15 |
14 |
13 |
16 |
15 |
10 |
9 |
12 |
11 |
10 |
9 |
12 |
11 |
|||
|
. |
||||||||||||||||||
|
2 |
4 |
1 |
3 |
2 |
4 |
1 |
3 |
6 |
8 |
5 |
7 |
6 |
8 |
5 |
7 |
|||
|
6 |
8 |
5 |
7 |
10 |
12 |
9 |
11 |
2 |
4 |
1 |
3 |
14 |
16 |
13 |
15 |
|||
|
10 |
12 |
9 |
11 |
6 |
8 |
5 |
7 |
14 |
16 |
13 |
15 |
2 |
4 |
1 |
3 |
|||
|
14 |
16 |
13 |
15 |
14 |
16 |
13 |
15 |
10 |
12 |
9 |
11 |
10 |
12 |
9 |
11 |
To change any reversible square to the corresponding most- perfect magic square, follow this procedure:
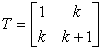
In this example , the first principle reversible square for order-4 (also shown above)
is shown with its transformation to a most-perfect magic square. The Transform for the
last column (in this case) is
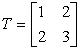
| Principle reversible square | Reverse half rows | Reverse half columns | Apply Transform to get the most- perfect square. | |||||||||||||||
| 1 | 2 | 3 | 4 | 1 | 2 | 4 | 3 | 1 | 2 | 4 | 3 | 1 | 15 | 4 | 14 | |||
| 5 | 6 | 7 | 8 | 5 | 6 | 8 | 7 | 5 | 6 | 8 | 7 | 8 | 10 | 5 | 11 | |||
| 9 | 10 | 11 | 12 | 9 | 10 | 12 | 11 | 13 | 14 | 16 | 15 | 13 | 3 | 16 | 2 | |||
| 13 | 14 | 15 | 16 | 13 | 14 | 16 | 15 | 9 | 10 | 12 | 11 | 12 | 6 | 9 | 7 | |||
| Order n |
Principle reversible sqr. Nn |
Variation of each Mn=2n-2{(1/2n)!}2 Mn |
Total reversible squares and most-perfect magic squares Nn x Mn |
| 4 | 3 | 16 | 48 |
| 8 | 10 | 36864 | 368640 |
| 12 | 42 | 5.30842 x 108 | 2.22953 x 1010 |
| 16 | 35 | 2.66355 x 1013 | 9.32243 x 1014 |
| 32 | 126 | 4.70045 x 1035 | 5.92256 x 1037 |
|
This square is most-perfect because
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
This pandiagonal magic square is not most-perfect. Pairs of integers distant ½n along a diagonal do not sum to T (although all 2 x 2 sets of cells sum to 2T). However, it is interesting because it contains 32 bent diagonals that sum correctly to 260.
All most-perfect magic squares are pandiagonal. Not all pandiagonal magic squares are most-perfect. |
![]()
And finally, an order-12 most-perfect magic square [1]
65 |
93 |
82 |
95 |
49 |
78 |
68 |
64 |
51 |
62 |
84 |
79 |
32 |
100 |
15 |
98 |
48 |
115 |
29 |
129 |
46 |
131 |
13 |
114 |
25 |
133 |
42 |
135 |
9 |
118 |
28 |
104 |
11 |
102 |
44 |
119 |
24 |
108 |
7 |
106 |
40 |
123 |
21 |
137 |
38 |
139 |
5 |
122 |
17 |
141 |
34 |
143 |
1 |
126 |
20 |
112 |
3 |
110 |
36 |
127 |
76 |
56 |
59 |
54 |
92 |
71 |
73 |
85 |
90 |
87 |
57 |
70 |
77 |
81 |
94 |
83 |
61 |
66 |
80 |
52 |
63 |
50 |
96 |
67 |
116 |
16 |
99 |
14 |
132 |
31 |
113 |
45 |
130 |
47 |
97 |
30 |
117 |
41 |
134 |
43 |
101 |
26 |
120 |
12 |
103 |
10 |
136 |
27 |
124 |
8 |
107 |
6 |
140 |
23 |
121 |
37 |
138 |
39 |
105 |
22 |
| 125 | 33 | 142 | 35 | 109 | 18 | 128 | 4 | 111 | 2 | 144 | 19 |
| 72 | 60 | 55 | 58 | 88 | 75 | 69 | 89 | 86 | 91 | 53 | 74 |
[1] Kathleen Ollerenshaw and David Brée, Most-perfect Pandiagonal Magic Squares, Institute of Mathematics and its Applications, 1988, 0-905091-06-X, page 20
When Kathleen Ollerenshaw introduced most-perfect magic squares in 1986 [1], she was referring to additive magic squares. However, the concept may be extended to multiply magic squares with suitable adaptation of the 3 basic requirements.
This addendum, is inspired
by the work on multiply magic squares in Christian Boyer’s recently posted
update. [2]
In it, I will demonstrate several multiply magic squares which I consider are
most-perfect. I will leave for others, a discussion and investigation of the
equivalent to Ollerenshaw’s “reversible magic squares”.
|
Requirements for most-perfect additive M.S. |
Requirements for most-perfect multiply M.S. |
|
|
|
The sum for the 2x2 cells has the same ratio to the magic constant as 4 cells are to the order of the square. For example, an order 4 square has 4 cells so the two sums are the same. For an order 8 square, the sum of the 2z2 arrays are 4:8 or 1/2 the magic constant. |
The exponent of the product for the 4 numbers in the 2x2 arrays is the ratio of the 4 cells to the order of the square. For example, for an order 4 multiply square the ratio is 1:1 so the product for each array is equal to the magic constant. For an order 6, the ratio is 4:6, so the magic constant is equal to the power 1.5 of the order 2 array. For an order 8 MMS, the product of the 4 cells of the 2x2 array squared equals the magic product of the square |
![]()
Sqr 1 Additive m.s.[3] Sqr 2 Multiplicative m.s.[4] 1 8 10 15 01 24 10 60 12 13 3 6 30 20 3 8 7 2 16 9 12 2 120 5 14 11 5 4 40 15 4 6 S=34 P=14,400
Sqr 1
All 48 additive pandiagonal magic squares are most perfect. However, in higher
orders, all pandiagonal magic squares are not most-perfect.
Most-perfect features
(requirements)
As per condition 1, all 2x2 blocks of cells sum to 34 which equals 2(1+16).
As per condition 2, diagonal pairs (such as 13+4) sum to 17 (which is the sum of
the first and last numbers used in the series).
If we add the sums of the 2 pairs we obtain the Magic sum of the square.
Sqr 2
This multiplicative magic square is
not normal, so the number of such squares is infinite! I assume that all such
squares of order 4 are most-perfect. Can anyone find a counter-example?
NOTE: for more theory and examples of Multiply magic hypercubes, see my cube-multiply page.
Most-perfect features
As per condition 1, product of the 4 cells in a 2x2 block = 14400 which is equal
to (1x120)2
As per condition 2, the product of diagonal pairs (such as 20 x 6) is 120 (which
is the product of the first and last numbers used in the series). If we
multiply the two products (of the 2 pairs) we obtain the magic product of the
square i.e. 1202 = 14,400..
![]()
Order 6 multiply magic squares
6x6 pandiagonal additive magic squares (using consecutive integers) are impossible. But because multiply magic squares cannot use consecutive integers, 6x6 pandiagonal multiplicative magic squares are possible!
Sqr 3 Harry A. Sayles,1913 [5]
729 192 9 46656 3 576
32 486 2592 2 7776 162
11664 12 144 2916 48 36
1 15552 81 64 243 5184
23328 6 288 1458 96 18
16 972 1296 4 3888 324
P = 101,559,956,668,416, Max. # = 46,656
Most-perfect features
As per condition 1, product of the 4 cells in a 2x2 block =2,176,782,336.
Because the ratio of the 4 cells in a 2x2 block to the 6 cells in a line (i.e.
4:6 or 1:1.5), 2,176,782,336 1.5 = 101,559,956,668,416, the magic
constant.
(The previous line may not be too eligible, so, to express it
differently, the product of the 4 cells is raised by the power 1.5 to equal the
product of the 6 cells.)
As per condition 2, the product of diagonal pairs (such as 486 x 96) is 46,656
(which is the product of the first and last numbers used in the series). Raising
this value to the 3rd power gives us the magic product. Again we are dealing
with ratios, because in an order 6 additive most-perfect m.s. we would multiply
the sum of the three diagonal pairs by 3.
As an added bonus, the products of all 3x3 blocks (9 cells) also equal a
constant value. This, of course, has no relevance to the most-perfect
designation.
Sqr 4 Christian Boyer, 2006 [2] 5 720 160 45 80 1440 4800 12 150 192 300 6 9 400 288 25 144 800 320 180 10 2880 20 90 75 48 2400 3 1200 96 576 100 18 1600 36 50 P = 2,985,984,000,000, Max. # = 4,800
The above multiplicative, most-perfect magic square has the smallest known
product P, more than 30 times smaller than P of the Sayles's example. And it has
also the same 2x2 and 3x3 sub-squares features.
Interestingly, Christian produced another square (not shown here) , also with
the same features, with a smaller maximum number but a larger P (4,410 and
85,766,121,000,000).
Most perfect features of Sqr 4 are:
As per condition 1, product of the 4 cells in a 2x2 block =
207,360,000.
This, when raised by the power 1.5 equals the magic product.
As per condition 2, the product of diagonal pairs (such as 12 x 1200) = 1st
times last number (3 x 4800) = 14,400. And 14,4003 =
2,985,984,000,000.
[1] Ollerenshaw,K. (1986) On ‘most perfect’ or ‘complete’ 8 x 8 pandiagonal magic squares. Proceedings of the Royal Society of
London A407, p.259-281
[2] Christian Boyer Update of October, 2006--Multiply magic squares
[3] One of the 48 order 4 pandiagonal magic squares published posthumously in 1691 as part of Frenicle de Bessy’s list of 880 order 4 magic squares.
[4] W.S. Andrews Magic Squares and Cubes, 2nd Edition, 1917. (Harry A. Sayles, p. 288. fig. 540. This was first published in : The Monist, 23, 1913, pp 631-640)
[5] ibid MS&C, 292, fig. 560[
![]()
Shown here is a pandiagonal magic square published in 1917 by L. S. Pierson. [1]
|
Recently Gil Lamb (Thailand) pointed out to me that this square has all the features of a Most-perfect magic square, except that it does not consist of consecutive numbers (a condition impossible in a singly even pandiagonal magic square). Note that |
01 47 06 43 05 48 35 17 30 21 31 16 36 12 41 08 40 13 07 45 02 49 03 44 29 19 34 15 33 20 42 10 37 14 38 09 |
[1] W.S. Andrews Magic Squares and Cubes, 2nd Edition, 1917, (L. S. Pierson) 238, fig. 393
![]()

![]() Please send me Feedback about my Web site!
Please send me Feedback about my Web site!
![]()
![]()
![]()
Harvey Heinz harveyheinz@shaw.ca
Last modified
December 31, 2008
Copyright © 2000 by Harvey D. Heinz