
The Principles of Optical Interferometry
Light from an unresolved astronomical source is collected with several separated mirrors and brought together at one or more detectors. A simple example with two mirrors and two detectors is shown in Figure 1.

Figure 1 – Simple astronomical optical interferometer
If the optical path length from the star along the beams is the same, the two beams will be coherent when they meet at the beam splitter shown in Figure 1. The beam splitter inverts the phase of the reflected beams without altering the phase of the transmitted beams. Optical interference between the light beams produces a difference in the observed intensity at the two detectors.
With a coherent point source, adjusting the delay shown in Figure 1 would change the path length of beam 2. Beams 1 and 2 would then move in and out of phase with each other, producing alternating constructive and destructive interference, as the interference fringes are scanned past the detector. The phase and amplitude of these oscillations are combined in a complex number called the complex fringe amplitude. The amplitude (magnitude) of this number is proportional to the amplitude of the oscillations, and the phase (argument) of this complex number is equal to the phase of the fringes measured relative to a predefined position. With an incoherent point source the amplitude of the fringes decreases as the absolute path difference between the two beams is increased. This is shown schematically in Figure 2. The characteristic length scale on which this occurs is the coherence length of the light, and is determined by the spectral bandwidth of the detectors. If the light in both beams is travelling in a non-dispersive medium, or if both beams are equally dispersed, there will be an optimal delay length where destructive interference occurs at all wavelengths simultaneously. This will not be the case if one of the beams has been dispersed more than the other.
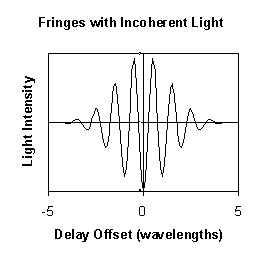

Figure 2 – Fringes observed using Figure 3 – Oscillation of delay line at 10 Hz
incoherent light (fractional bandwidth ~0.4)
At the COAST array, there are four input beams from four separated 40mm telescopes, each with a separate delay line. Interference fringes are observed by oscillating the delay lines backwards and forwards about the ideal delay length, and recording the variation in intensity. The beam combining arrangement transmits one quarter of each beam to each of four photon counting avalanche photo-diode (APD) detectors. Lenses are used to focus the light from each of the telescope apertures onto the detectors, ensuring that under ideal atmospheric conditions all incoming starlight passing through one aperture would interfere constructively at the detector. The bandwidth sensitivity of the detectors is constrained using optical filters. Fluctuations in the atmosphere cause additional variation in the optical path lengths along the beams. These fluctuations typically become significant on timescales greater than about twenty milliseconds. If the complex amplitude of the interference fringes on one of the baselines is to be measured, one of the delay lines on this baseline is modulated with a 10Hz sawtooth wave (Figure 3). A measurement of the fringe phase is attempted in each half cycle of this sawtooth or "sweep". In order to perform the phase measurement, the output of an APD must be digitally sampled at a higher rate than the Nyquist frequency of the fringes. The data is separated into individual sweeps, and in each sweep the phase of the Fourier component at the expected fringe frequency is taken as an estimate of the fringe phase in the sweep.
The principle sources of noise affecting fringe complex amplitude measurements of monochromatic sources are as follows:
In measurements of astronomical light sources, changes in the atmospheric optical path length create different phase errors at each of the telescopes. The phase error induced in the measured complex fringe amplitude will be the difference between the atmospheric phase errors applied to each of the incoming beams:
![]()
where
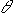 1 and
1 and 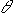 2 are the uncorrupted phases of the incoming
beams, e
1 and e
2 are the atmospheric errors and
2 are the uncorrupted phases of the incoming
beams, e
1 and e
2 are the atmospheric errors and
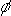 1,2 is the phase of the complex fringe amplitude.
1,2 is the phase of the complex fringe amplitude.
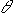 1 -
1 - 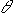 2 corresponds to one Fourier component of the sky brightness distribution, and accurate measurement of this parameter at a variety of different
telescope separations would allow an image of the source to be formed. Unfortunately, the atmospheric errors e
1 and e
2 are usually too great for this technique to be used on ground based telescopes.
2 corresponds to one Fourier component of the sky brightness distribution, and accurate measurement of this parameter at a variety of different
telescope separations would allow an image of the source to be formed. Unfortunately, the atmospheric errors e
1 and e
2 are usually too great for this technique to be used on ground based telescopes.
In order to overcome these atmospheric effects, at least three beams must be used from three separate telescopes. Each of the possible pairs of telescopes is called a baseline. At COAST, complex fringe amplitude measurements can be performed simultaneously on all three baselines when there are three input beams. The complex fringe amplitudes can then be multiplied together to form the complex closure amplitude, a useful observable parameter. The phase of this parameter will be the sum of the phases of each of the complex fringe amplitudes:
![]()
As the optical path length fluctuations induced by the atmosphere are in the near field (they are very much closer to the telescopes than the astronomical source), the fluctuations in one beam will produce equal and opposite phase errors in the two complex fringe amplitude measurements which involve this beam. The phase of the complex closure amplitude (Jennison’s closure phase) is thus unaffected by phase errors applied in the near field of the telescope. If many complex closure amplitude measurements are made with a variety of telescope separations, an image of the source can be made.
With an incoherent chromatic source these closure relations apply at each individual wavelength within the source spectrum. If the light intensity detectors are linear and have finite spectral bandwidth, the closure relations will apply if light of the same spectral composition is used in complex fringe amplitude measurements on each of the three baselines.
The error induced in closure phase measurements when light of different spectral composition is used on each of the baselines is determined by the degree of optical dispersion in each of the incoming beams. If each of the incoming beams is equally dispersed, no error will result. The effect of dispersion on closure phase measurements is discussed further in Section 8.
As the bandwidth of the optical filters used at COAST is very much greater than the digital sampling rate and the astronomical sources observed usually provide a small number of photons per sample, the probability of two photons occupying a single energy state is extremely small. The boson-boson quantum mechanical interference between photons will thus have very little effect on the observed intensity, and in most situations the photons can be treated as independent particles. This means that the number of photons detected in any given time interval should follow a Poisson-distributed probability distribution with mean value equal to the integrated intensity over that time period.
If the photon shot noise and detector noise at any particular time are not influenced by the light intensity at any other time, these effects will only add pure white noise to the observed signal. As most of the processing of intensities is performed in the Fourier domain, the photon shot noise and background counts will generally only contribute random errors to measured parameters. These errors can be reduced through the use of long integration times.
Return to Bob's Interferometry Page.
Return to Bob's Home Page.