Prefacio
Del prefacio del autor a la tercera edición rusa
1. La quinta operación matemática
2. El idioma del álgebra
3. En ayuda de la aritmética
4. Las ecuaciones de Diofanto
5. La sexta operación matemática
6. Ecuaciones de segundo grado
7. La magnitud mayor y la menor
8. Progresiones
9. La séptima operación matemática
Bajar Documento Completo

Capitulo Séptimo
LA MAGNITUD MAYOR Y LA MENOR
Contenido
1. Dos trenes
2. ¿Dónde construir el apeadero?
3. ¿Cómo trazar la carretera al embarcadero?
4. ¿Cuándo alcanza el producto su máximo valor?
5. ¿Qué suma será la menor?
6. El tronco de mayor volumen
7. Dos parcelas de tierra
8. La cometa
9. La construcción de una casa
10. La parcela
11. El canalón de sección máxima
12. El embudo de mayor capacidad
13. La iluminación más intensa
Los problemas presentados en este capítulo pertenecen a una clase muy interesante; con ellos se propone hallar el valor mayor o el menor de cierta magnitud. Estos problemas pueden ser resueltos por diferentes procedimientos, uno de los cuales exponemos a continuación.
P. Chebyshev, matemático ruso, en su obra "Delineación de los mapas geográficos" escribía que los métodos, que ayudaban a resolver un problema común para toda la actividad práctica del hombre - cómo disponer de sus medios para obtener, en la medida de lo posible, mayor provecho tienen una importancia especial.
1. Dos trenes
Problema
Dos líneas férreas se cruzan formando un ángulo recto. Los trenes se acercan a gran velocidad hacia el cruce. Uno parte de cierta estación situada a 40 km del cruce; el otro, de una estación que dista 50 km del cruce. El primero marcha a una velocidad de 800 m por minuto, el segundo a 600 m ¿Cuántos minutos transcurrirán desde el momento de la partida para que las locomotoras se hallen a la menor distancia entre sí, y cuál será esa distancia?
Solución
Dibujemos el esquema de la marcha de los trenes. Supongamos que las líneas rectas AB y CD son dos líneas férreas que se cruzan (fig. 19 . ) La estación B se encuentra a 40 km del cruce O , y la estación, D a 50 km. Admitamos que al cabo de x minutos los trenes se encuentran a la distancia más próxima entre sí: (MN = m). El tren que sale de B hace el recorrido BM = 0,8 x , ya que en un minuto recorre 800 m = 0,8 km. Por consiguiente, OM = 40 - 0,8 x . Del mismo modo hallaremos que ON = 50 - 0,6 x . Según el teorema de Pitágoras
Elevemos al cuadrado ambas partes de la ecuación
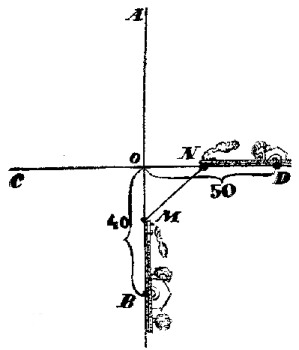
|
| Figura 19. |
Resolviendo la ecuación para hallar el valor de x , resultará
Ya que x , el número que expresa los minutos transcurridos, no puede ser una raíz imaginaria, entonces m 2 -256 debe ser una magnitud positiva o, a llo sumo, equivalente a cero. El último es el que corresponde al valor mínimo de m; de aquí que:
Es evidente que m no puede ser menor que 16, de lo contrario x se convertiría en una raíz imaginaria. Y si m 2 – 256 = 0, entonces x = 62.
De esta forma las locomotoras llegan a su punto de mayor aproximación al cabo de 62 minutos, y la distancia que las separa será de 16 km. Determinemos dónde se encontrará cada una en el momento de mayor aproximación. Al buscar la distancia OM, tendremos que es igual a
El signo negativo indica que la primera locomotora habrá rebasado el cruce en 9,6 km. La distancia ON será:
Es decir, que a la segunda locomotora le faltarán 12,8 km para llegar al cruce. En la fig. 20 se ve la posición que ocupan las locomotoras en el momento dado. Se puede apreciar que ésta no es tal y como nos la imaginábamos al principio.
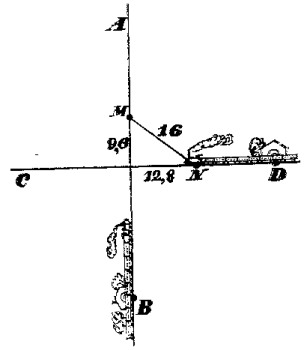
|
| Figura 20. |
La ecuación ha resultado ser tan tolerante que, a pesar de lo erróneo del esquema, nos da un resultado acertado. No es difícil averiguar de dónde proviene esa tolerancia, que está condicionada por las reglas algebraicas de los signos.
Volver
2. ¿Dónde construir el apeadero?
Problema
A 20 km del ferrocarril, cuya línea es recta, se encuentra el punto poblado B (fig. 21).
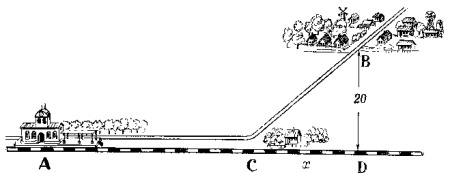
|
| Figura 21 |
¿Dónde hay que construir el apeadero C para que en el viaje de A a B por la línea férrea AC, y por la carretera CB se invierta el menor tiempo posible? La velocidad por ferrocarril es de 0,8 y por carretera de 0,2 kilómetros por minuto.
Solución
Expresemos la distancia AD (desde A hasta la base de la perpendicular BD a la horizontal AD ) con la a; y CD, con la x . Entonces
El tiempo empleado por el tren para cubrir el trayecto AC será igual a
El tiempo necesario para recorrer la distancia CB de la carretera equivale a
El viaje desde A hasta B ocupará, en total,
Esta suma, que expresamos con m, debe ser la menor.
La ecuación
preséntase así:
Multiplicando por 0,8 tendremos
Y cuando expresamos 0,8 m - a , con la k , haciendo desaparecer el radical, tendremos la ecuación de segundo grado
de donde
Y como k = 0, 8 m - a, al alcanzar m la mínima magnitud sucede lo mismo con la k, y viceversa. Mas para que x resulte real es necesario que 16 k 2 no sea menor que 96 000. Por lo tanto, el valor mínimo para 16 k 2 será 96 000. Por esa razón, m será la magnitud menor cuando 116 k 2 = 96000,
de donde
y por consiguiente
El apeadero debe construirse aproximadamente a 5 km del punto D cualquiera sea la longitud a = AD.
No obstante, es evidente que nuestra solución tiene sentido sólo en el caso de x < a, pues al formular la ecuación hemos considerado que la expresión a - x era un valor positivo.
Si x = a » 5,16 no hace falta ningún apeadero y debe llevarse la carretera hasta la estación. De manera idéntica hay que operar en los casos en que la distancia a sea inferior a 5,16 km.
Esta vez somos nosotros los que hemos obrado con mayor prudencia que la ecuación. Si hubiéramos confiado ciegamente en la ecuación, habríamos tenido que construir el apeadero más allá de la estación, cosa totalmente absurda: en este caso x>a, por eso, el tiempo a-x/ 0,8
durante el cual teníamos que viajar en ferrocarril, sería negativo. El caso es aleccionador y muestra que, al valerse de recursos matemáticos hay que mantener una actitud prudente hacia los resultados obtenidos, recordando siempre que si no se cumplen las condiciones en las que se fundamenta el empleo del recurso matemático, el resultado puede perder todo sentido.
Volver
3. ¿Cómo trazar la carretera al embarcadero?
Problema
Desde la ciudad ribereña A hay que trasladar cargamento al punto B, situado a a km más abajo, y a d km de la orilla del río (fig. 22).
¿Cómo debe trazarse la carretera desde B al río para que el transporte de cargas desde A hasta B resulte lo más barato posible, considerando que el transporte de una tonelada-kilómetro por río cuesta la mitad que por carretera?
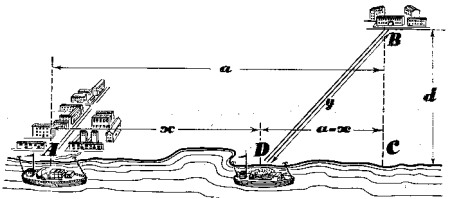
|
| Figura 22 |
Solución
Expresaremos la distancia AD con la x, y la longitud de la carretera DB con la y . Como hemos supuesto, la longitud AC = a, y la BC = d. Puesto que el transporte por carretera cuesta el doble que por río, la suma
debe ser, respondiendo a las exigencias del problema, la más pequeña. Expresémosla con la m . De aquí la ecuación
y
entonces la ecuación se presentará así:
y, al hacer desaparecer el radical, resulta:
Resolvamos ahora la ecuación:
Para que y responda a las condiciones, ( m - a ) 2 no debe ser inferior a 3 d 2 . La magnitud más pequeña de ( m - a ) 2 es igual a 3 d 2 y entonces
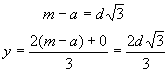
es decir,
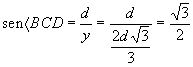
Mas el ángulo cuyo seno es igual a Ö 3/2 equivale a 60°. Esto significa que la carretera debe ser trazada formando un ángulo de 60° con el río, independiente de la distancia AC.
Aquí vuelve a aparecer la misma particularidad que en el problema anterior. El resultado tiene sentido sólo en determinadas condiciones. Si el punto poblado está situado de tal manera que la carretera (cuya línea forma un ángulo de 60° con la del río) pasa por el lado opuesto de la ciudad A, entonces la solución dada es inaplicable; en este caso hay que unir directamente el punto B con la ciudad A por carretera sin emplear en absoluto el río para el transporte.
Volver
4. ¿Cuándo alcanza el producto su máximo valor?
Problema
Para resolver muchos problemas relacionados con "el máximo y el mínimo", es decir, para buscar el valor mayor y el menor de una magnitud variable, puede emplearse un teorema algebraico que examinaremos a continuación. Veamos el problema siguiente:
¿En qué dos partes debe dividirse un número para que su producto alcance el máximo valor?
Solución
Supongamos que el número dado sea a . Las partes en que se divide a son
El número x indica la diferencia de estas partes con la mitad de a. El producto de ellas es igual a
Es evidente que el producto de las partes tomadas aumentará en la medida en que disminuya x , es decir, en la medida en que disminuya la diferencia entre las mismas. El resultado mayor será cuando x = 0, es decir, cuando ambas partes sean iguales a a /2
Quedarnos, pues, en que el número debe dividirse por la mitad. El producto de dos números, cuya suma sea constante alcanzará su máximo valor cuando estos números sean iguales entre sí.
Examinemos este mismo ejemplo con tres números.
Problema
¿En qué tres partes debe dividirse un número para que su producto alcance el máximo valor?
Solución
Para resolver este problema nos apoyaremos en el anterior.
Tomemos un número a dividido en tres partes. Supongamos previamente que ninguna de las tres partes es igual a a / 3- Entre ellas habrá una parte mayor que a / 3 (las tres no pueden ser menores que a / 3). Dicha parte la expresaremos así:
También habrá otra parte menor que a /3 que representaremos con
Los números x e y son positivos. La parte tercera será indudablemente igual a
es mayor que el producto de las dos primeras partes del número a .
De esta forma, si las dos primeras partes del número a son sustituidas por los números
dejando la tercera intacta, el producto aumentará.
Supongamos ahora que una de las partes es igual a a /3 . Entonces las otras dos partes se presentarán así
Si hacemos que estas dos partes sean iguales a a /3 (cuya suma, por ello, no se altera), veremos que su producto aumenta, siendo igual a:
Así pues, si el número a se divide en tres partes desiguales, el producto de éstas será menor que a 3 /27 es decir, menor que el producto de tres factores iguales que sumen a .
Por el mismo procedimiento puede demostrarse este teorema para cuatro factores, para cinco, etc.
Examinemos ahora un caso más general.
Problema
Hállese el valor de x y de y para que la expresión x p *y q alcance la mayor magnitud si x+ y = a.
Solución
Busquemos el valor de x mediante el cual la expresión
alcance su máxima magnitud.
Multipliquemos esta expresión por 1/ x p *y q y obtendremos la siguiente:
que alcanzará su máxima magnitud cuando la adquiera la expresión inicial.
Representemos así a la expresión obtenida
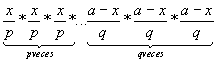
La suma de todos los factores será igual a
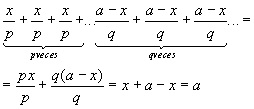
es decir, será una magnitud constante.
Si nos basamos en lo demostrado anteriormente deduciremos que el producto
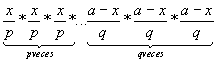
alcanza el máximo valor al ser iguales sus factores, es decir, cuando
Sabemos que a – x = y ; sustituyendo el antecedente de la segunda razón y alterando el orden de los medios, resultará
De esta forma, el producto de x p *y q alcanza su máximo valor, si la suma x+ y es constante, cuando
Siguiendo semejante razonamiento puede demostrarse que los productos
Volver
5. ¿Qué suma será la menor?
El lector que desee abordar la demostración de teoremas algebraicos de valor práctico, puede demostrar por sí mismo el siguiente principio:
- La suma de dos números, cuyo producto es constante, alcanza el valor mínimo cuando dichos números son iguales. Por ejemplo, para el producto 36 : 4 + 9 = 13, 3 + 12 = 15, 2 + 18 = 20, 1 + 36 = 37 y, por último, 6 + 6 = 12.
- La suma de varios números, cuyo producto es invariable, será la menor cuando las magnitudes de los números dados sean idénticas. Por ejemplo, para 216: 3 + 12 + 6 = 21, 2 + 18 + 6 = 26, 9 + 6 + 4 = 19, mientras que 6 + 6 + 6 = 18.
Volver
6. El tronco de mayor volumen
Problema
De un tronco cilíndrico debe sacarse una viga rectangular del máximo volumen. ¿Qué forma ha de tener su sección? (fig. 23)

|
| Figura 23 |
Solución
De acuerdo con el teorema de Pitágoras, si los lados de la sección rectangular son x e y , tendremos
Donde d es el diámetro del tronco. El volumen de la viga será el máximo cuando la superficie de su sección sea también la mayor, es decir, cuando xy alcance la mayor magnitud. Mas si xy tiene su máximo valor, también lo alcanzará x 2 y 2 . Y como la suma x 2 + y 2 es constante, el producto x 2 y 2 será el mayor, como demostramos antes, cuando
Por lo tanto, la sección de la viga debe ser cuadrada.
Volver
7. Dos parcelas de tierra
Problemas
- ¿Qué forma ha de tener una parcela rectangular de un área dada, para que la longitud de su cerca sea la menor posible?
- ¿Qué forma debe tener una parcela rectangular para que, con una longitud fija de su cercado, tenga aquélla la mayor área posible?
-
La forma de la parcela rectangular se determina por la relación entre sus
lados,
x
e
y.
El área de una parcela cuyos lados sean
x
e
y es igual a
xy,
y la longitud de la cerca 2
x
+ 2
y
. Esta última será la menor si
x + y
tiene el menor valor.
Si el producto
xy
es constante, la suma
x
+
y
es la menor si
x = y.
Por lo tanto, el rectángulo que buscamos debe ser un cuadrado.
- Si x e y son los lados de una parcela rectangular, la longitud de su cerca será 2 x + 2 y , y su área, xy . Este producto es el mayor cuando lo es también el producto 4 xy , o sea, 2 x *2 y ; este último alcanza su máximo valor (si la suma de sus factores 2 x + 2 y es constante) cuando 2 x = 2 y , es decir, si la parcela es un cuadrado.
Volver
8. La cometa
Problema
Búsquese la forma de una cometa con un sector circular que tenga la mayor superficie, partiendo de un perímetro previamente dado.
Solución
Precisadas las condiciones del problema, debemos hallar la relación entre la longitud del arco del sector y su radio que nos de la mayor superficie posible, sin alterar el perímetro dado.
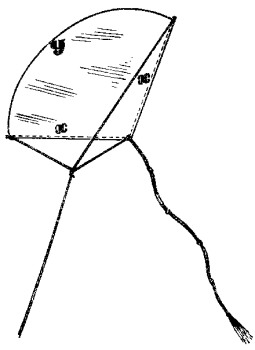
Si el radio de un sector es x y el arco y , el perímetro 1 y la superficie S , se expresarán así (fig. 24).
|
| Figura 24 |
S = xy/ 2 = x(I - 2 x) /2
La magnitud de S llega a su máximo valor, con los valores de x que lo proporcionen también a la expresión 2 x (1- 2 x), o sea, el cuádruplo de la superficie, Y como la suma 2 x+ (1- 2 x) = l es una magnitud constante, su producto será el mayor cuando 2x= l -2x, de donde
y = l – 2 * l /4 = l /2
De esta forma, un sector con perímetro dado tiene la mayor superficie cuando su radio representa la mitad del arco (es decir, la longitud de su arco es igual a la suma de los radios; o la longitud de la línea curva de su perímetro es igual a la longitud de la quebrada). El ángulo del sector es aproximadamente de 115°, o sea, dos radianes. Las cualidades de vuelo de tal cometa ya es una cuestión ajena a este problema.
Volver
9. La construcción de una casa
Problema
En el solar de una casa derruida, donde queda en pie tan sólo una pared de 12 m de largo, se proyecta la construcción de un nuevo edificio aprovechando el muro existente. La superficie de la nueva casa debe ser de 112 m 2 . Las condiciones económicas para la obra son:
- La reparación de un metro lineal de pared vieja equivale al 25% de lo que cuesta levantar una nueva.
- El derribo de un metro lineal de la pared vieja y la construcción de una nueva con ladrillo recobrado alcanza el 50% de lo que costaría levantarla con material de fábrica.
Solución
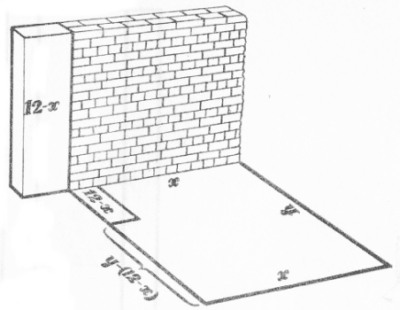
Supongamos que se conservan x metros de pared y los demás 12- x se derriban para, con el material recuperado, levantar una parte de la pared de la futura casa (fig. 25).
|
| Figura 25 |
Si el valor de cada metro lineal levantado con ladrillo nuevo es igual a a, la reparación de x metros de pared vieja costará ax /4 ; la edificación de los 12- x metros de pared costará a (12-x)/ 2; el resto de la pared, a [ y - (12 - x )], es decir, a ( y+x-12 ); la tercera parte de la pared, ax , y la cuarta, ay . Todo el trabajo equivaldrá a
La última expresión llegará a su mínima magnitud cuando la suma 7 x + 8 y alcance su valor mínimo.
Sabemos que el área de esta casa xy es igual a 112; por lo tanto,
Si el producto es constante, la suma 7 x * 8 y tomará el menor valor cuando
de donde
Sustituyendo el valor de y en la ecuación xy = 112
tendremos:
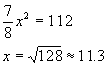
Y siendo la longitud de la antigua pared de 12 m debe desmontarse tan sólo 0,7 m de dicha pared.
Volver
10. La parcela
Problema
Con el fin de construir una casa de campo se precisaba cercar la pared destinada a este fin. Contábase con material para l metros lineales de valla. Además, en uno de los lados de la parcela podía emplearse una cerca construida con anterioridad.
En estas condiciones, ¿cómo hubo que cercar la parcela rectangular para abarcar la mayor superficie posible?
Solución
Supongamos que la longitud de la parcela (según la cerca) es igual a x, y el ancho (es decir, la dimensión de la parcela en la dirección perpendicular a la cerca) equivale a y (fig. 26).

|
| Figura 26 |
En este caso, para cercar esta parcela fueron precisos x +2 y metros de cerca, de forma que
El área de la parcela será
que alcanzará un valor máximo simultáneamente con el valor 2 y ( l - 2 y ) (duplo del área), producto de dos factores, siendo l constante. Por eso, para conseguir la mayor área de la parcela, debe tener lugar la siguiente igualdad
de donde
En otras palabras: x = 2 y , es decir, la longitud de la parcela debe ser el doble de la anchura.
Volver
11. El canalón de sección máxima
Problema
Hemos de doblar en forma de canalón una hoja rectangular de chapa (fig. 27).

|
| Figura 27 |

|
| Figura 28. |
¿Cuál ha de ser la anchura de los costados y qué ángulo deben formar para que la sección del canalón tenga la máxima superficie? (fig. 29).

|
| Figura 29. |
Solución
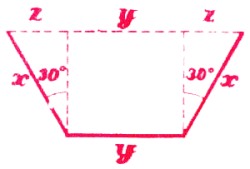
Representemos por l la anchura de la hoja; por x, la de los costados doblados, y por y la del fondo del canalón. Introduzcamos una medida más, la incógnita z , cuyo valor aparece con toda claridad en la fig. 30.
|
| Figura 30. |
La superficie del trapecio que representa la sección del canalón será
La tarea consiste en determinar cuáles han de ser los valores de x, y, z para que S alcance la mayor magnitud admitiendo que la suma 2 x + y (anchura de la hoja) es una constante l. Pasemos a las transformaciones:
S 2 alcanzará su máxima magnitud con los valores de x, y y z que la proporcionen también a 3S2.
3 S 2 puede presentarse en forma de producto
La suma de estos factores será:
es decir, es invariable. Por eso, el producto de nuestros cuatro factores llega al máximo cuando éstos son iguales entre sí, es decir
x + z = 3 x - 3 z.
Por la primera ecuación sabemos que
y como
entonces
De la segunda ecuación, resulta
Como el cateto z es igual a la mitad de la hipotenusa x (fig. 30), el ángulo opuesto a este cateto será igual a 30°, y el ángulo de inclinación de los costados equivaldrá a 90° + 30° = 120°.
En fin, el canalón alcanzará la mayor sección cuando sus dobleces tengan la forma de 3 lados contiguos de un hexágono regular.
Volver
12. El embudo de mayor capacidad
Problema
Debemos construir la parte cónica de un embudo valiéndonos de un círculo de hojalata. Para ello se corta un sector en dicho círculo y, con el resto, se construye el cono (fig. 31).

|
| Figura 31 |
¿Cuántos grados debe tener el arco del sector que se ha cortado para que el embudo alcance la mayor capacidad posible?
Solución
La longitud del arco de aquella parte que se aprovecha para el cono se representa con la x (en unidades lineales). Por lo tanto, la generatriz será el radio, R , del círculo de hojalata, y la circunferencia de la base será igual a x. El radio r , de la base del cono, se determinará en la igualdad
de donde
La altura del cono, según el teorema de Pitágoras, será (fig. 31).
El volumen de este cono equivaldrá a
Y esta expresión alcanza su mayor valor simultáneamente con la expresión
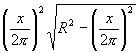
y con su cuadrado
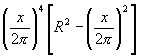
y como
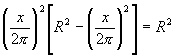
es un valor constante, el último producto (como se demuestra en las páginas anteriores) llega a su máximo valor cuando x tiene una magnitud tal, que
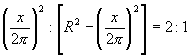
de donde
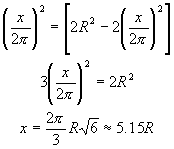
El arco x tiene alrededor de 295° y, en consecuencia, el arco del sector cortado equivaldrá aproximadamente a 65 grados.
Volver
13. La iluminación más intensa
Problema
¿A qué altura de la mesa debe hallarse la llama de una vela para que ilumine con la mayor intensidad a una moneda colocada sobre dicha mesa?
Solución
Puede parecer que para conseguir el objetivo propuesto deba colocarse la llama lo más baja posible. Esto es falso. En esas condiciones, los rayos de luz caen muy oblicuos. Mas si se eleva la vela para que los rayos caigan más verticales, el foco de luz se aleja. Por eso, la iluminación más ventajosa es, sin duda, la que se realiza desde una altura media.
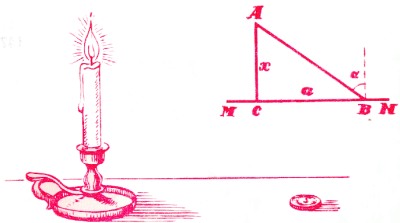
|
| Figura 32 |
Denominemos a esta altura con la letra x (fig. 32). La distancia BC, que media entre la moneda B y la base C de la perpendicular que pasa por la llama A, la designaremos con la letra a . Si la claridad de la llama es i , de acuerdo con las leyes de la óptica, la luminosidad será expresada así:
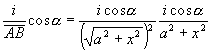
donde a es el ángulo de caída de los rayos AB. Y como
a luminosidad será
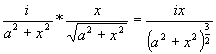
Esta expresión alcanza su máximo valor cuando sin variar la x, adquiera también su mayor magnitud el cuadrado de aquélla
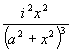
Omitamos el valor del factor i 2 por su magnitud constante y transformemos el resto de la expresión analizada como sigue:
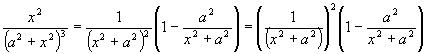
La expresión transformada alcanza su mayor magnitud cuando la alcanza la expresión
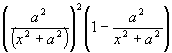
por cuanto el factor constante introducido, a 4 , no influye en el valor de x con el cual el producto llega a su más elevada magnitud.
Partiendo de que la suma de las primeras potencias de estos factores
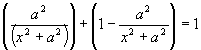
es una magnitud constante, se deduce que el producto examinado alcanza su más alto valor cuando
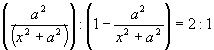
Tenemos una ecuación:
que al resolverla resultará
La moneda es iluminada con la mayor intensidad cuando el foco de luz se encuentra a una altura de 0,71 de la distancia desde la proyección del foco hasta la moneda. El conocimiento de esta correlación ayuda a instalar con la mayor acierto el alumbrado en los lugares de trabajo.
Volver
|
|
|
|